Poisson-Rauschen

In der Analyse von RNA-Seq-Daten arbeiten wird mit Count-Matrizen. Die “Messwerte” sind keine Messungen (measurements), sondern Anzahlen (counts): Wie viele Reads wurden in Probe X gezqhlt, die von Gen Y stammten?

Wann immer wir Zähl-Daten (count values) haben, mússen wir uns mit der Besonderheit von Zähl-Statistiken beschaftigen.

Wiederholung: Binomialverteilung

Beispiel: Wir möchten wissen, ob es der Anteil Blauäugiger in der Bevölkerung Manngheims anders ist als in Heidelberg. Wir wählen zufällg je 30 Mannheimer und Heidelberger aus: 13 der 30 Mannheimer und 9 der 30 Heidelberger haben blaue Augen.

Vier-Felder-Tafel:

m <- rbind( c( 13, 17 ), c( 9, 21 ) )
dimnames(m) <- list( c( "Mannheim", "Heidelberg" ), c( "blau", "nicht-blau" ) )
m

           blau nicht-blau
Mannheim     13         17
Heidelberg    9         21

Ist das ein signifikanter Unterschied?

fisher.test(m)

    Fisher's Exact Test for Count Data

data:  m
p-value = 0.422
alternative hypothesis: true odds ratio is not equal to 1
95 percent confidence interval:
 0.5447005 5.9528841
sample estimates:
odds ratio 
  1.767024 

Nein.

Um uns das plausibel zu machen, modellieren wir das Problem: Wenn der Anteil Blauäuigiger in Deutschland 30% beträgt, und wir 30 Personen zufällig auswählen, wie viele Blauäugige finden wir?

Wir sehen uns die Binomial-Verteilung für \(n=30\) und \(p=0.3\) an:

plot( 0:20, dbinom( 0:20, 30, .3 ), type="h" )

Poisson-Limit der Binomialverteilung

Die Binomialverteilung hat zwei Parameter: \(n\) und \(p\).

Für sehr kleines \(p\) hängt die Verteilung nur vom Produkt \(\lambda=np\) ab.

Beispiel: Die Binomialverteilungen zu \(n=10\,000\), \(p=0.001\) und \(n=100\,000\), \(p=0.0001\) sehen praktisch gleich aus:

library(tidyverse)

tibble( k=0:25 ) %>%
mutate(
  prob1 = dbinom( k,  1000, .01 ),
  prob2 = dbinom( k, 10000, .001 ) ) %>%
ggplot() +
  geom_col( aes( x=k, y=prob1 ), fill="orange", alpha=.5 ) +
  geom_col( aes( x=k, y=prob2 ), fill="steelblue", alpha=.5 )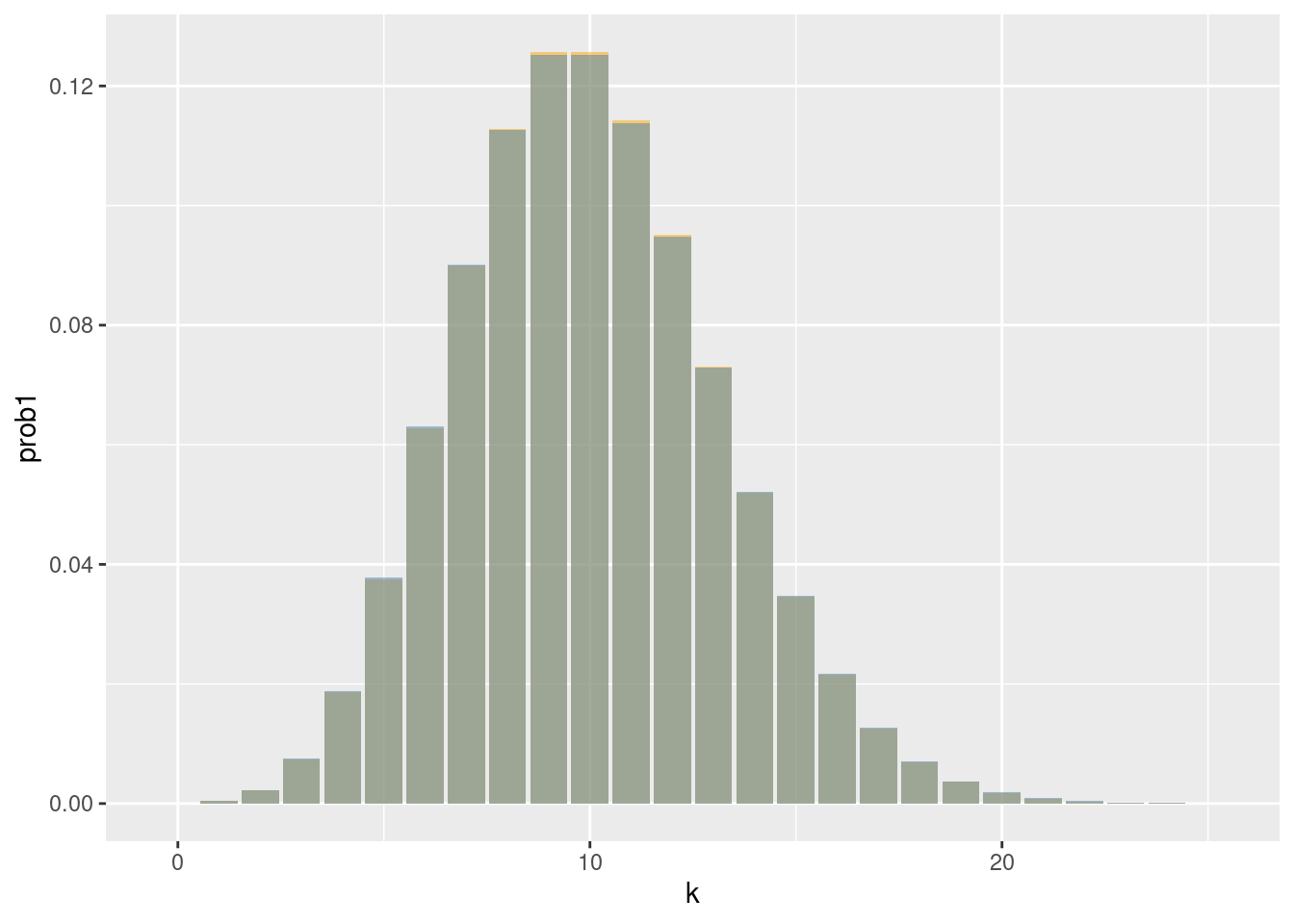 

Allgemein: Zwei Binomialverteilungen \(\text{Bi}(n_1,p_1)\) und \(\text{Bi}(n_2,p_2)\) mit demselben Erwartungswert \(\mu = n_1p_1 = n_2p_2\) sehen fast gleich aus, wenn \(p_1\ll 1\) und \(p_1\ll 2\).

Für einen vorgegebenen Erwartungswert \(\mu\) nähern sich die Binomialverteilungen \(\text{Bi}(n,p)\) mit \(p=\mu/n\) für \(n\to\infty\) einer Grenzverteilung an, der Poisson-Verteilung \(\text{Pois}(\mu)\), mit der Wahrscheinlichkeitsverteilung \[ f_\text{Pois}(k|\mu) = e^{-\mu}\frac{\mu^k}{k!}. \]

Eine explizite Rechnung ergibt dies als den Grenzwert für \(\n\to\infty\) für \(f_\text{Bi}(k|n,p)=\binom{n}{p}p^k(1-p)^{n-k}\) mit \(p=\frac{\mu}{n}\) ist.

Poissonverteilung als exakte Verteilung

Auf einen gepflasterten Platz fällt ein kurzer Regenschauer. Die Intensitqt ist so, dass pro Quadratmeter im Mittel 40 Tropfen fallen. Wir betrachten einen Pflasterstein mit 0.25 m² Fläche. Wir erwaten also, 10 Tropfen vorzufinden. Wie wahrscheinlich ist es, dass wir auf dem Stein \(k\) Tropfen zählen?

Antwort: Die Tropfenzahl ist Poisson-verteilt mit \(\mu=10\).

plot( 0:20, dpois( 0:20, 10 ), type="h" )

Vergleiche: Wenn wir insgesamt 1000 Pflastersteine haben, die somit \(n=10000\) Tropfen aufsammeln, hätten wir für die Tropfen auf einem Stein eine Binomialverteilung \(\text{Bi}(10000,.001)\), die fast gleich der Poissonverteilung ist.

Diesmal ist aber die Poissonverteilung nicht nur Näherung, sondern exakt, den \(n\) ist nicht vorgegeben.

Standardabweichung der Poissonverteilung

Die Standardabweichung von \(\text{Bi}(n,p)\) ist \(\sigma=\sqrt{np(1-p)}\). Für \(p\ll 1\) und \(\mu=np\) ist das \(\sigma\approx\sqrt{\mu}\).

Für die Poissonverteilung gilt das exakt:

Eine Poissonverteilung mit Erwartungswert \(\mu\) hat Varianz \(v=\mu\) und STandardabweichung \(\sigma=\sqrt{\mu}\).

Beispiel: Mit einem Zählgitter zählen wir die Anzahl Leukozyten in einem Tropfen verdünnten Blutes. Wir zählen 20 Zellen innerhalb der Zählkammer. Dann untersuchen wir eine zweite Probe und zählen 25 Tropfen. Dürfen wir folgern, dass die Leukozyten-Konzentration in der zweiten Probe größer ist?

Für einen Erwartungswert von 20 beträgt die Poisson-Standardabweichung \(\sqrt{20}=4.5\) und für haben wir \(\sqrt{25}=5\). Der Standardfehler unser Zahlen ist also nicht kleiner als die Differenz.

Wenn wir also die Konzentration genau genug bestimmen möchten, so dass wir einen Unterschied von 25% zuverlässig erkennen können, müssen wir deutlich mehr Zellen zählen.

Genauigkeit von Konzentrationen

Für eine STudie zur Wirksamkeit eines Herbizids soll für eine bestimmte Unkrautspezies die Anzahl der Pflanzen pro Quadratmeter besttimmt werden. Dazu werden an 20 Stellen im Acker jeweils ein Quadratmeter abgesteckt und die Pflanzen gezählt. Insgesamt haben wir (in allen 20 Quadraten zusammen) 237 Pflanzen gezählt. Das ergibt 237/20 = 11.8 Pflanzen pro m². Wie genau ist diese Angabe?

Die Standardabweichung unseres Zählergebnisses ist \(\sqrt{237}=15.4\). Das ist Standardfehler von \(15.4/20=0.8\) Pflanzen pro m².

Die relative Genauigkeit unseres Ergebnisses ist also \(0.8/11.8=7\%\).

Wenn wir die Genauigkeit auf verbessern möchten, z.B., um den Faktor 3, also auf 2.3%, dann müssen wir \(3^2=9\) mal so viele Pflanzen zählen, also statt 20 Quadraten 180 QUadrate auszählen.

Es gilt also (mal wieder): Um die Genauigkeit um den Faktor \(s\) zu verbessern, muss man die Stichprobe um den Faktor \(s^2\) vergrößern.

Besonderheit beim Zählen: Wir können die Genauigkeit direkt aus der gezählten Anzahl ablesen: Wir haben 237 Pflanzen gezählt und konnten daher die Anzahl pro m² mit einer Genauigkeit von \(1/\sqrt{237}=7\%\) bestimmen.

Eine Konzentration, die durch Abzählen von \(k\) Objekten ermittelt wurde hat eine Genauigkeit (relative Standardabweichung) von \(1/\sqrt{k}\).

Anwendung auf RNA-Seq

Beispiel 1: In einer Probe haben wir für Gen A 20 Reads gezählt und für Gen B 25 Reads. Können wir sagen, dass Gen B stärker exprimiert ist?

Nein.

Denn die Genauigkeit der Anzahlen beträgt nur etwa \(1/\sqrt{20}=22\%\) bzw. \(1/\sqrt{20}=20\%\) und der Unterschied ist auch \(25\%\) mehr (oder \(20\%\) weniger). Ein Vergleich, z.B. durch einen Hypothesentest auf Gleichheit von Anteilen (\(\chi^2\)-Test mit prop.test), wird also nicht signifikant sein.

Beispiel 2: In einem Experiment soll untersucht werden, welche Gene auf einen bestimmten Stimulus reagieren. Das Gen A ist von besonderem Interesse. Typischerweise hat Gen A eine Expressionsstärke von etwa 50 CPM. Wie tief muss sequenziert werden, dass man die Epxressionsstärke von Gen A auf 10% genau bestimmen kann?

Antwort: Um 10% Genauigkeit zu erhalten, muss man für das Gen 100 Reads zählen (denn \(1/\sqrt{100}=10\%\)). Wenn wir füë das Gen 50 CPM, also 50 Reads pro 1 Million Reads ingesamt, erwarten, sollten wir mindestens 2 Millionen Reads pro Probe anpeilen.

Beispiel 3: Wir möchten wissen, ob die Expressionsstärke von Gen A sich unterscheidet zwischen Hautproben von gesunden und von an Schuppenflechte erkrankten Probanden.

Wir haben folgende Daten:

set.seed( 13245768 )

tibble(
  group = rep( c( "healthy", "psoriatic" ), each=8 ),
  read_count_total = round( 10^rnorm( 16, 6.2, .3 ) )
) %>%
mutate(
  count_for_gene_A = rbinom( 16, read_count_total,
      rnorm( 16, 1e-4, 1e-5 ) * ifelse( group=="psoriasis", 2, 1 ) ) ) -> tbl

tbl %>% mutate( log2cpm = log2( count_for_gene_A / read_count_total * 1e6 )  ) -> tbl

tbl

# A tibble: 16 × 4
   group     read_count_total count_for_gene_A log2cpm
   <chr>                <dbl>            <int>   <dbl>
 1 healthy            1077696              108    6.65
 2 healthy             716249               58    6.34
 3 healthy             940125               76    6.34
 4 healthy            2477479              218    6.46
 5 healthy             519908               51    6.62
 6 healthy            3468998              312    6.49
 7 healthy            2626134              250    6.57
 8 healthy             852788              100    6.87
 9 psoriatic          2007456              179    6.48
10 psoriatic          1919857              153    6.32
11 psoriatic          2894769              361    6.96
12 psoriatic           752304               88    6.87
13 psoriatic          8368364              734    6.45
14 psoriatic          1065549              111    6.70
15 psoriatic           719314               69    6.58
16 psoriatic          2796383              257    6.52

Die Genauigkeit der CPM-Werte beträgt also um 10% da die Zählwerte um 100 liegen.

Der Effekt von Psoriasis wurde so simuliert, dass die Genexpression verdoppelt wird.

Können wir differentielle Genexpression nachweisen? Wir machen einen t-Test:

t.test( log2cpm ~ group, tbl )

    Welch Two Sample t-test

data:  log2cpm by group
t = -0.69546, df = 13.411, p-value = 0.4986
alternative hypothesis: true difference in means between group healthy and group psoriatic is not equal to 0
95 percent confidence interval:
 -0.2839887  0.1453464
sample estimates:
  mean in group healthy mean in group psoriatic 
               6.542015                6.611336 

Warum hat die Genauigkeit von 10% nicht gereicht um eine Verdopplung (Änderung um 100%) zu erkennen?

Weil 10% nur die technische Variabilität ist. Die biologische Variabilität (Unterschiede zwischen Probanden in derselben Gruppe) war viel höher.

Also: Bei schwach exprimierten Genen limitiert das Poisson-Rauschen (technische Variabilität) die statistische Power, bei stark exprimierten Genen ist die biologische Variabilität der limitierende Faktor.

Zusammenfassung

Wann immer man in einer Stichprobe zählt, liegt Poisson-Rauschen vor, dass die Genauigkeit des Ergebnisses beschränkt.

Wenn man \(k\) Objekte in einem Volumen \(V\) zählt (dass eine Probe darstellt, die aus einer viel größeren gesamtheit genommen wurde) und mann dann eine Konzentration \(c=k/V\) folgert, dann hat dieses Ergebnis eine relative Ungenauigkeit von \(1/\sqrt{k}\). Das bedeutet, dass das Verhältnis von ermitteltem Wert zu wahrem Wert mit einer Standardabweichung von \(1/\sqrt{k}\) um 1 “schwankt”.