Lineare Regression

Beispieldaten

Wir möchten wissen, ob das Gewicht eiens Samens einen Einfluss auf das Wachstum einer Pflanze hat. Wir wiegen 50 Samen, pflanzen sie ein, warten 4 Wochen, und messen dann die Höhe der Pflanze.

Der folgende Code erstellt Beispiel-Daten

library( tidyverse )
set.seed( 1325 )

tibble( seed_weight = rnorm( n=50, mean=50, sd=10 ) ) %>%
mutate( plant_height = rnorm( n=50, mean=30, sd=5 ) + 0.1*seed_weight ) -> plant_data

Unsere Samen wiegen also im Schnitt 50 mg mit Standardabweichung 10 mg. Die Pflanzen werden im Schnitt 30 cm hoch mit einer (vom Gewichtd es Samens unabhägigen) Standardabweichung von 5 cm. Dazu kommt ein Effekt von Effekt von 0.03 cm extra für jedes mg Samen-Gewicht.

Hier ist ein Plot:

ggplot(plant_data) + geom_point( aes( x=seed_weight, y=plant_height ) )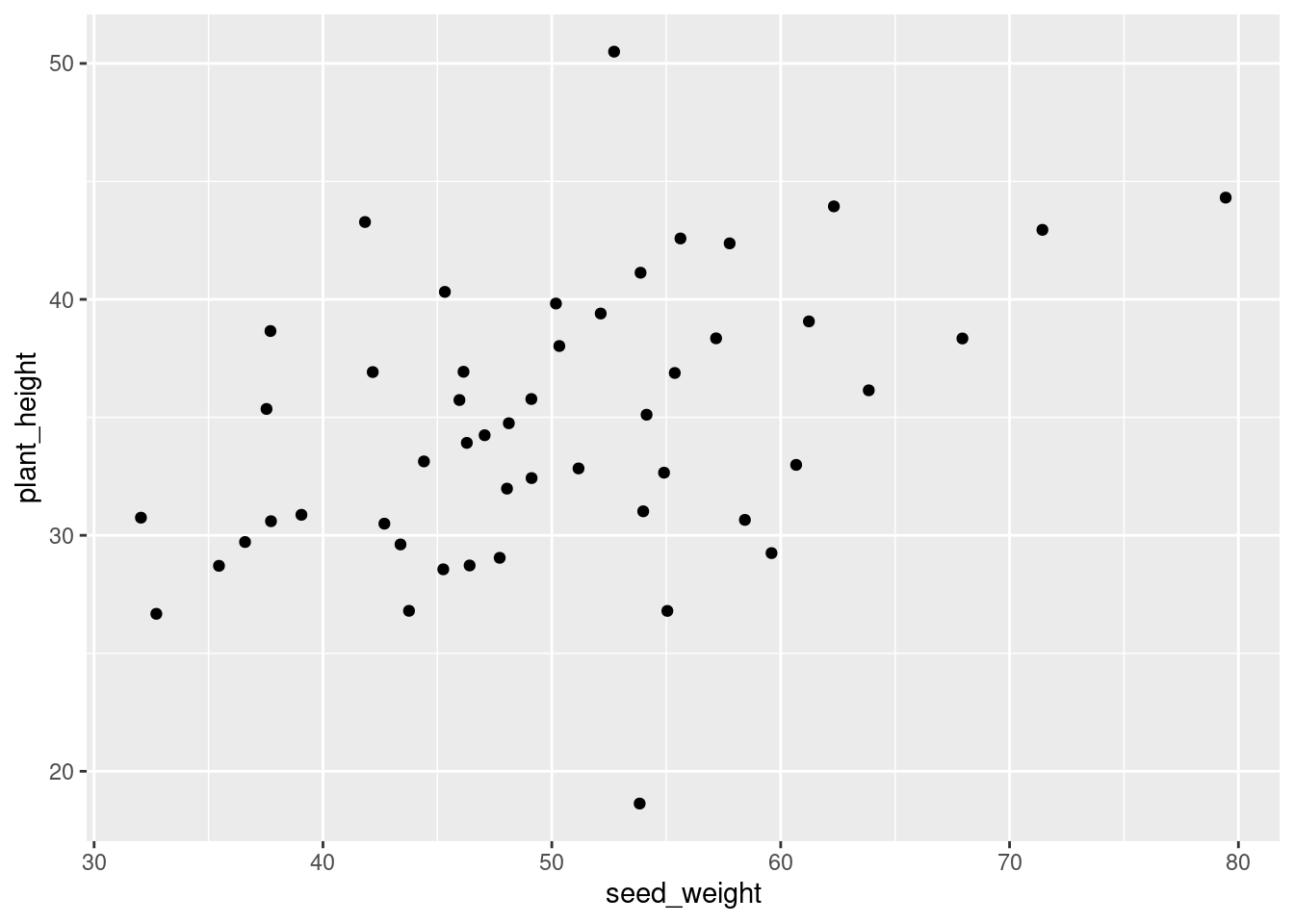

Fitten eines linearen Modells

fit <- lm( plant_height ~ seed_weight, plant_data )
fit

Call:
lm(formula = plant_height ~ seed_weight, data = plant_data)

Coefficients:
(Intercept)  seed_weight  
    22.3204       0.2482  

Die Werte der Koeffizienten können wir aus dem fit-Objekt entnehmen:

coef(fit)

(Intercept) seed_weight 
 22.3203968   0.2481968 

Unser Fit ergibt also folgende Formel für den fitted value für die Höhe \(y_i\) (in cm) von Pflanze \(i\):

\[ \hat y_i = 31.4 + 0.067 x_i, \] wobei \(x_i\) das Gewicht des Samens in mg ist.

Regressionsgerade

Wir zeichnen dies in unseren Plot ein:

ggplot(plant_data) + 
  geom_point( aes( x=seed_weight, y=plant_height ) ) +
  geom_abline( intercept = coef(fit)[["(Intercept)"]], slope = coef(fit)[["seed_weight"]] )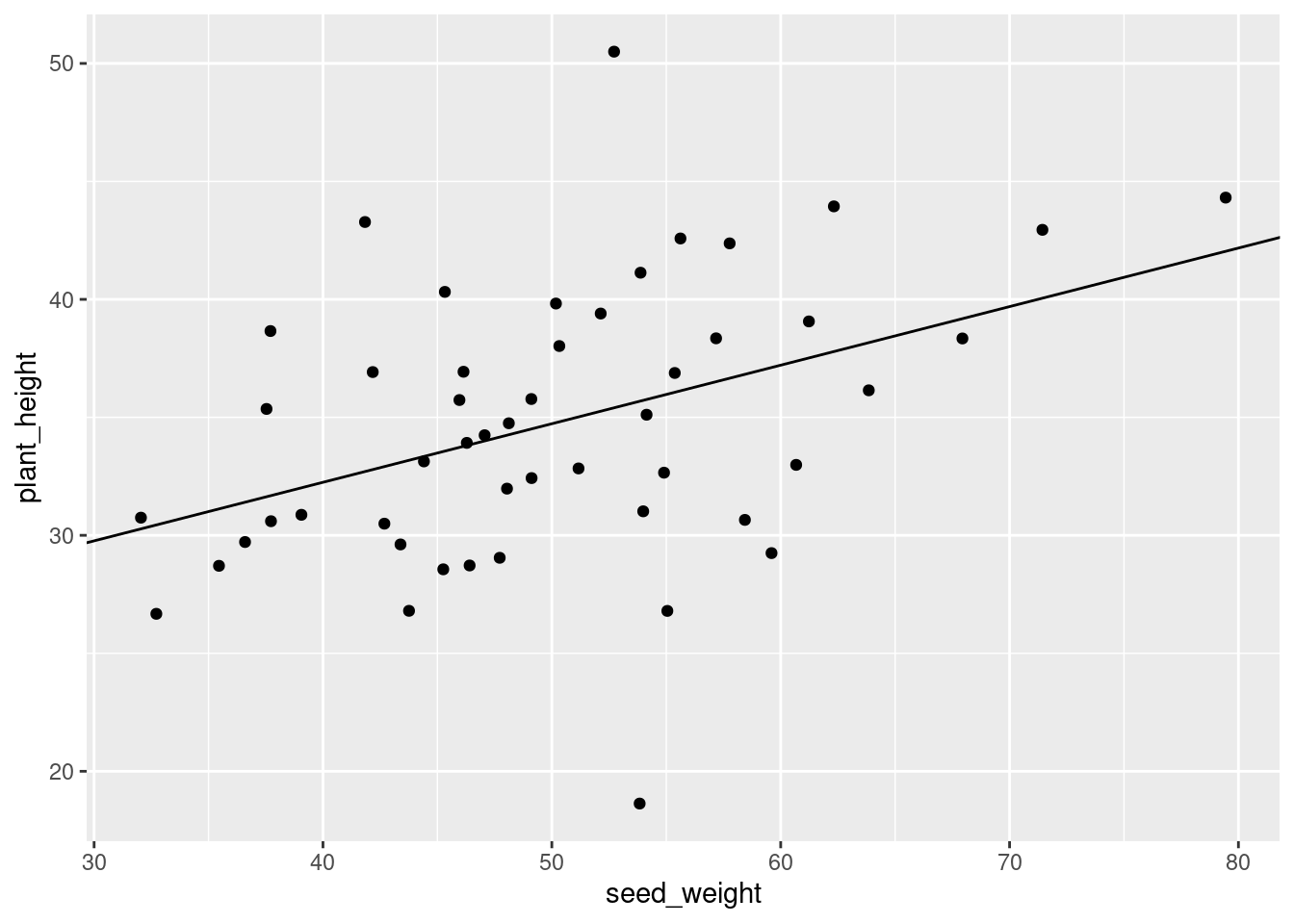

Diese Linie (“Ausgleichsgerade”, “Regressionsgerade”) ist den Daten angepasst (fitted to the data), in dem Sinne, dass die Residuen-Quadratsumme \(\text{RSS} = (y_i - \hat y_i)^2\) minimiert wurde.

Signifikanz

Wieviel Varianz wird erklärt, und ist das signifikant?

summary(fit)

Call:
lm(formula = plant_height ~ seed_weight, data = plant_data)

Residuals:
     Min       1Q   Median       3Q      Max 
-17.0506  -3.0742  -0.0505   3.1982  15.0927 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 22.32040    4.02404   5.547 1.22e-06 ***
seed_weight  0.24820    0.07886   3.147  0.00283 ** 
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 5.408 on 48 degrees of freedom
Multiple R-squared:  0.1711,    Adjusted R-squared:  0.1538 
F-statistic: 9.905 on 1 and 48 DF,  p-value: 0.002831

Ja.

Die Steigung ist aber deutlich zu groß. Wie immer sollten wir uns aber nicht auf die Punktschätzung verlassen, sondern ein Konfidenzintervall berechnen. Die Tabelle oben enthält bereits eine Standardfehler für den Koeffizienten, und die Funtion confint berechnet ein 95%-Konfidenzintervall:

confint( fit )

                  2.5 %     97.5 %
(Intercept) 14.22952988 30.4112637
seed_weight  0.08963603  0.4067577

Korrelationskoeffizient

Das Bestimmtheitsmaß \(R^2\), dass wir oben erhalten haben, ist das Quadrat des Pearson-Korrelationskoeffizienten:

cor( plant_data$seed_weight, plant_data$plant_height )

[1] 0.4135942

cor( plant_data$seed_weight, plant_data$plant_height )^2

[1] 0.1710602

Zur Erinnerung, die Formel für den Pearson-Korrelationskoeffizient einer Liste von Werte-Paaren \((x_i,y_i)\) mit Mittelwerten \(\mu_x\) unf \(\mu_y\):

\[ R = \frac{\sum_i (x_i-\mu_x)(y_i-\mu_y)}{\sqrt{\sum_i (x_i-\mu_x)^2\sum_i(y_i-\mu_y)^2}}\]

Code zum Testen

Hier ist der Code nochmal zusammen gestellt. Durch mehrfaches ausführen können wir sehen, wie das Ergebnis variieren kann.

tibble( seed_weight = rnorm( n=50, mean=50, sd=10 ) ) %>%
mutate( plant_height = rnorm( n=50, mean=30, sd=5 ) + 0.1*seed_weight ) -> plant_data

fit <- lm( plant_height ~ seed_weight, plant_data )

ggplot(plant_data) + 
  geom_point( aes( x=seed_weight, y=plant_height ) ) +
  geom_abline( intercept = coef(fit)[["(Intercept)"]], slope = coef(fit)[["seed_weight"]] )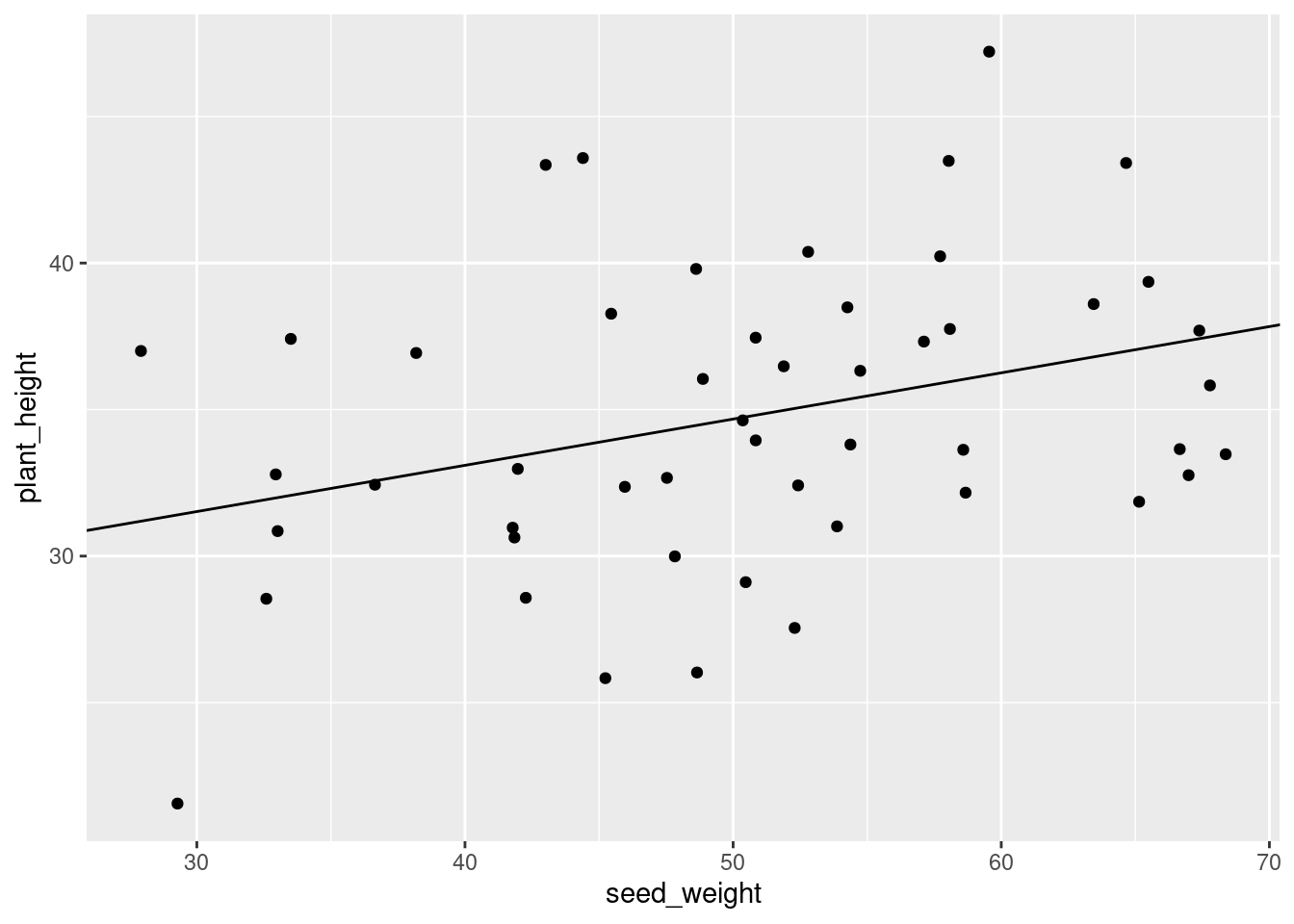

coef(fit)

(Intercept) seed_weight 
 26.7861615   0.1577994 

confint(fit)

                 2.5 %    97.5 %
(Intercept) 20.0805513 33.491772
seed_weight  0.0281757  0.287423

summary(fit)

Call:
lm(formula = plant_height ~ seed_weight, data = plant_data)

Residuals:
    Min      1Q  Median      3Q     Max 
-9.8517 -3.5876 -0.2836  3.0153 11.0303 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 26.78616    3.33507   8.032 1.97e-10 ***
seed_weight  0.15780    0.06447   2.448   0.0181 *  
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 4.889 on 48 degrees of freedom
Multiple R-squared:  0.111, Adjusted R-squared:  0.09244 
F-statistic: 5.991 on 1 and 48 DF,  p-value: 0.01809

Wachstum von Kindern

Wir laden die NHANES-Daten und filtern auf die Kinder (bis 15 Jahre):

read_csv( "data_on_git/nhanes.csv" ) %>%
filter( age < 16, !is.na(height) ) -> nhanes_children

Nun fitten wir ein lineares Modell:

fit <- lm( height ~ age, nhanes_children )
fit

Call:
lm(formula = height ~ age, data = nhanes_children)

Coefficients:
(Intercept)          age  
     81.799        6.058  

Wir plotten dies:

ggplot( nhanes_children ) +
  geom_point( aes( x=age, y=height, col=gender ), size=.3, position=position_jitter(width=.2,height=0) ) +
  geom_abline( intercept = coef(fit)["(Intercept)"], slope=coef(fit)["age"] )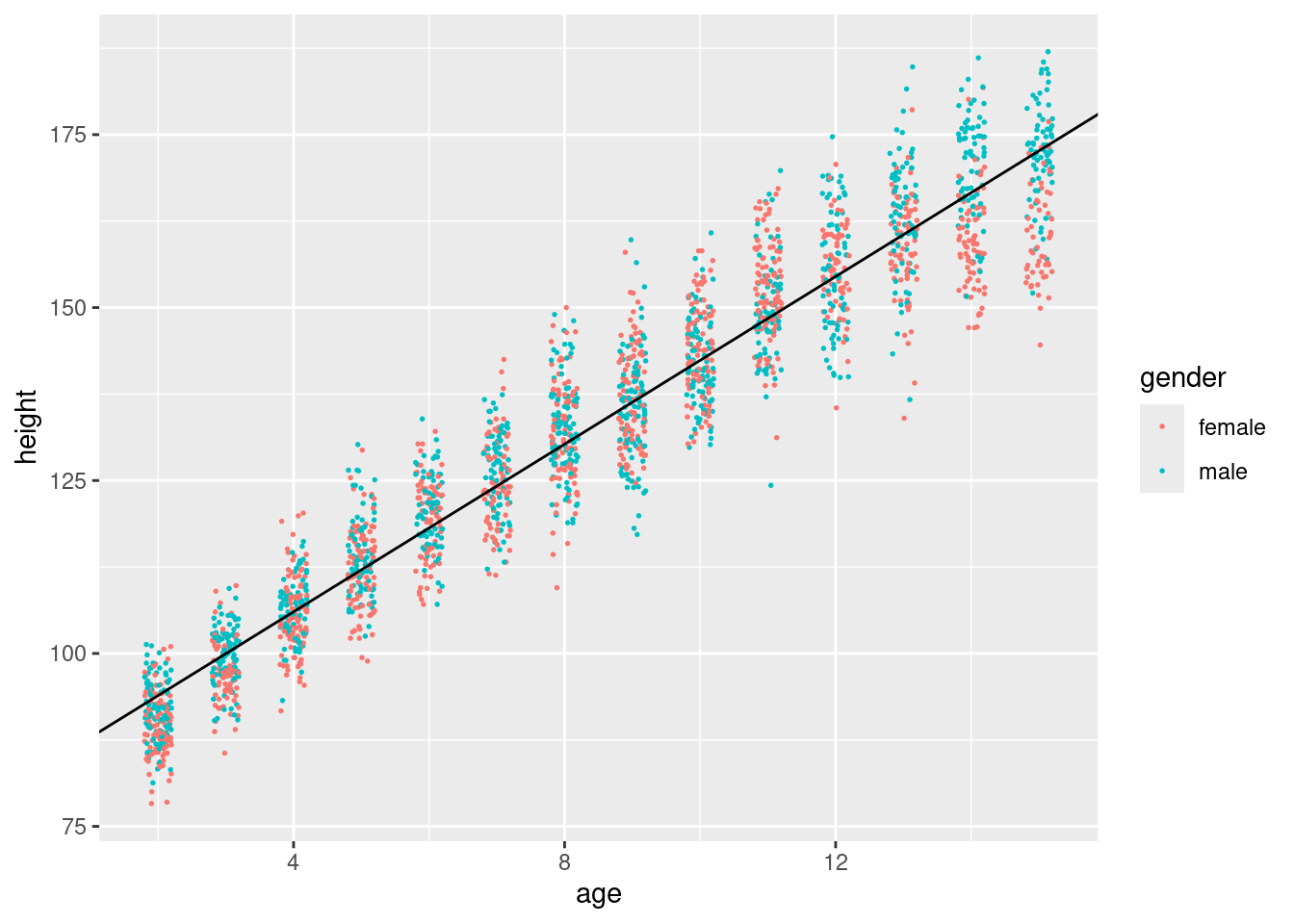

Kategorische und kontinuierliche Variable

Zurück zum Beispiel der Samen. Nun wurde die Hqlfte der Samen vorher getrocknet. Dies verringert den Wuchs:

set.seed( 1327 )

tibble( seed_weight = rnorm( n=50, mean=50, sd=15 ) ) %>%
mutate( dry = rep( c( "no", "yes" ), each=25 ) ) %>%
mutate( plant_height = rnorm( n=50, mean=30, sd=5 ) + 
          0.3*seed_weight + ifelse( dry=="yes", -.5, 0 ) ) -> plant_data

Wir möchten wissen, ob die Trocknung einen Unterschied macht.

Erster Versuch: t-Test

t.test( plant_height ~ dry, plant_data ) 

    Welch Two Sample t-test

data:  plant_height by dry
t = 2.0686, df = 43.475, p-value = 0.04457
alternative hypothesis: true difference in means between group no and group yes is not equal to 0
95 percent confidence interval:
 0.09254813 7.20059264
sample estimates:
 mean in group no mean in group yes 
         46.76732          43.12075 

Signifikant, aber nur gerade eben.

Ein Plot zeigt, warum:

ggplot(plant_data) + geom_point( aes( x=seed_weight, y=plant_height, col=dry ) )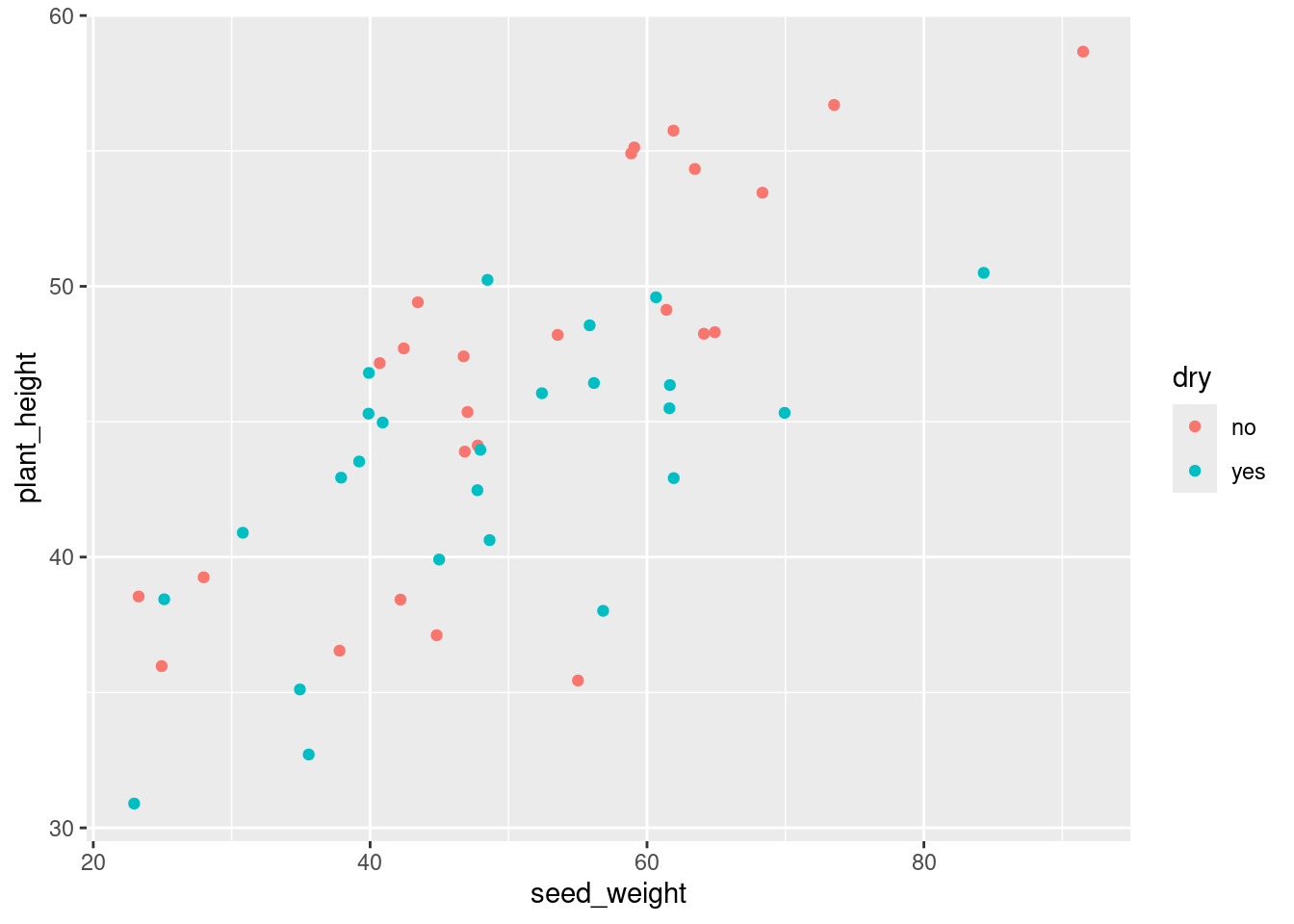

Wenn wir erst seed_weight “heraus-regressieren” (to regress out), und die Residuen vergleichen würden, sollten wir ein klareres Ergebnis bekommen:

anova( lm( plant_height ~ dry + seed_weight, plant_data ) )

Analysis of Variance Table

Response: plant_height
            Df Sum Sq Mean Sq F value    Pr(>F)    
dry          1 166.22  166.22  8.8477  0.004621 ** 
seed_weight  1 981.63  981.63 52.2515 3.683e-09 ***
Residuals   47 882.97   18.79                      
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1