library( tidyverse )
library( ggbeeswarm )
set.seed( 13245768 )Konfidenzintervalle für Mittelwerte und t-Tests
Standardfehler des Mittelwerts
Wiederholung:
Gegeben sei eine Zufallsgröße mit Erwartungswert (d.h. Mittelwert in der Grundgesamtheit) \(\mu\) und Standardabweichung (der Grundgesamtheit) \(\sigma\). Wir ziehen \(n\) Werte (d.h. wir entnehmen der Grundgesamtheit \(n\) zufällig ausgewählte Elemente) und bestimmen deren Mittelwert \(\hat\mu\).
Die Standardabweichung des Stichprobenmittelwerts vom Erwartungswert, genannt der “Standardfehler des Mittelwerts” (standard error of the mean, SEM), beträgt dann \(\text{SEM} = \sigma /\sqrt{n}\).
Beispiel 1
Die Grundgesamtheit sei eine Normalverteilung mit \(\mu=10\) und \(\sigma=3\). Wir ziehen \(n=25\) Werte:
rnorm( 25, mean=10, sd=3 ) -> x
x [1] 8.324963 6.550638 7.731856 11.940100 5.159262 13.402040 12.193168
[8] 7.308412 11.026460 10.832688 12.616139 6.763932 17.226406 8.275735
[15] 6.569186 12.465967 16.254203 9.698572 7.255427 7.460184 12.060542
[22] 5.934219 12.356365 13.671730 10.309631Nun bestimmen wir den Mittelwert:
mean(x)[1] 10.13551Wir simulieren, dass dieses Experiment 10000 mal wiederholt wird:
replicate( 10000, {
rnorm( 25, mean=10, sd=3 ) -> x
mean( x )
} ) -> many_means Hier ist ein Histogramm der Einzelwerte und der Mittelwerte:
breaks <- seq( -3, 23, length.out=100 )
hist( rnorm( 10000, mean=10, sd=3 ), freq=FALSE, breaks=breaks, main="Einzelwerte in Grundgesamtheit" ) 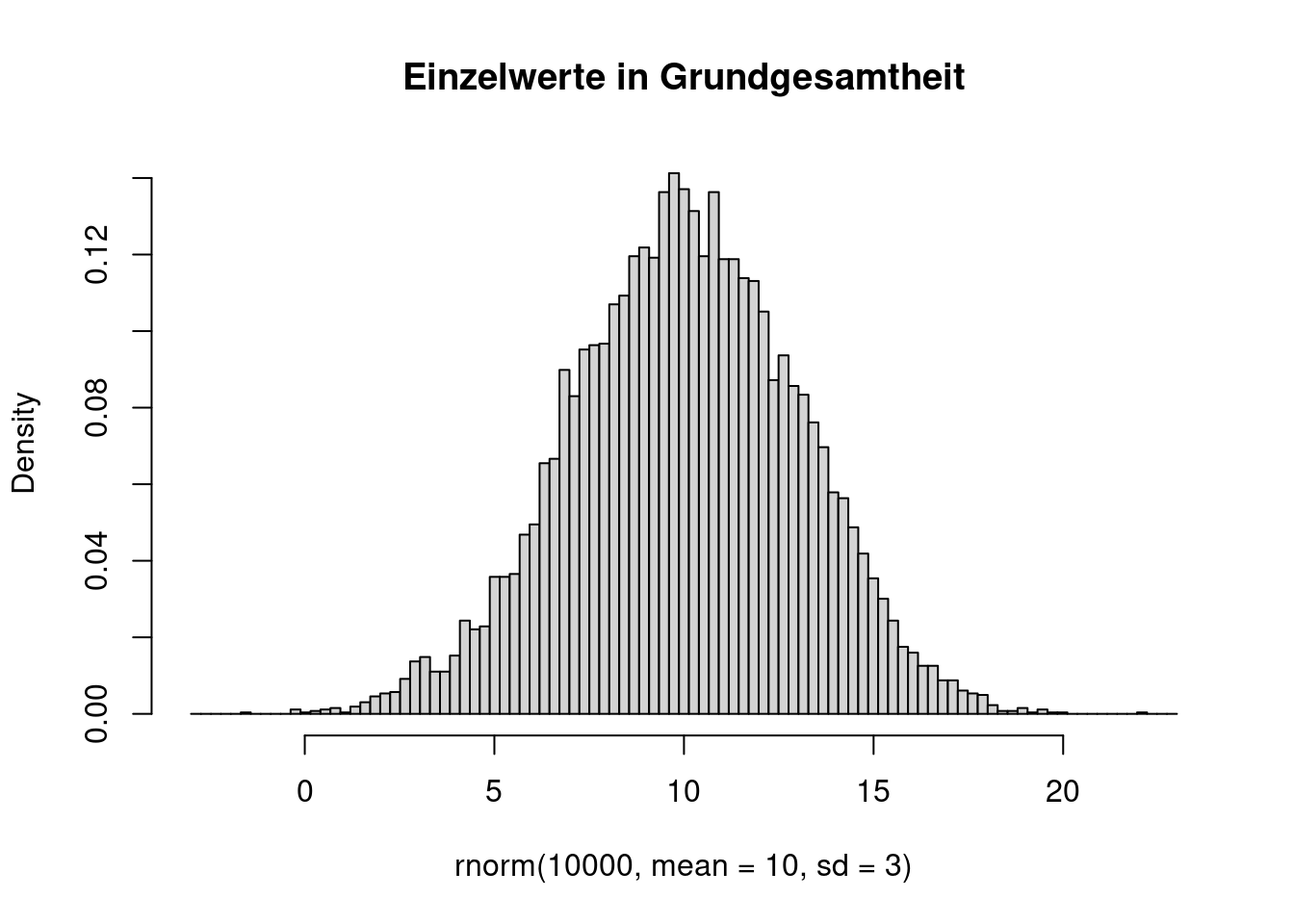
hist( many_means, freq=FALSE, breaks=breaks, main="Mittelwerte von je 25 Einzelwerten" ) 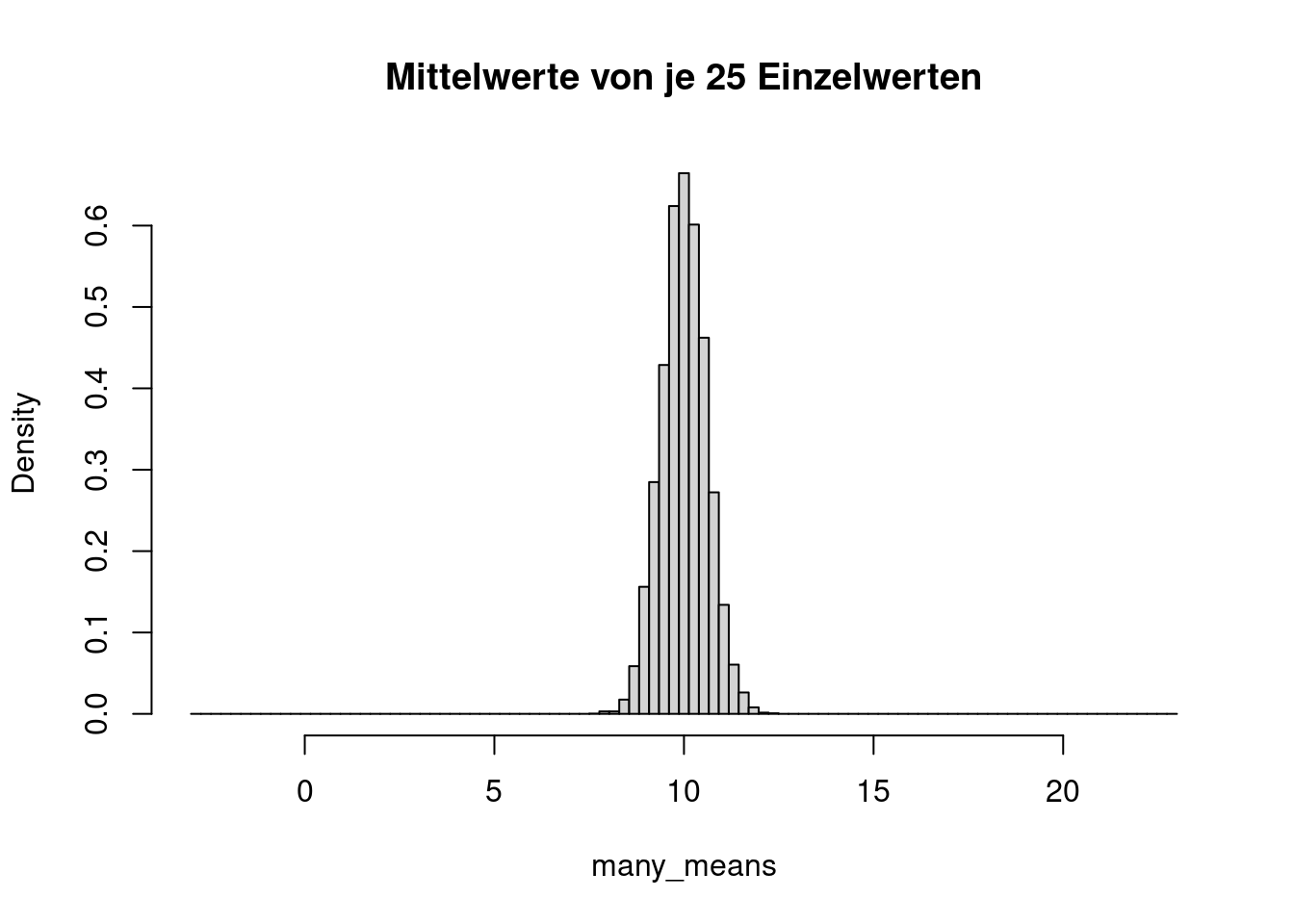
Die Verteilung der Mittelwerte ist um den Faktor \(\sqrt{n}=5\) schmäler als die Verteilung der Einzelwerte.
SEM mit Stichproben-Standardabweichung
In der Praxis wissen wir die Standardabweichung der Grundgesamtheit nicht. Wir müssen sie aus der Stichprobe schätzen.
Beispiel, wie zuvor: 25 Werte gezogen aus \(\mathcal{N}(10,3)\)
rnorm( 25, mean=10, sd=3 ) -> x
mean( x ) [1] 10.13269sd( x )[1] 2.488519Wir schätzen für den SEM
sd(x) / sqrt(25)[1] 0.4977038und geben daher als Mittelwert an: 10.13 ± 0.50
Der angegebene Bereich schließt den wahren Mittelwert ein.
Ist das eine zuverlässige Methode? Wir probieren das 10000 mal aus:
replicate( 10000, {
rnorm( 25, mean=10, sd=3 ) -> x
c( mean=mean(x), sem=sd(x)/5 )
}) %>% t -> many_means_with_sem
head( many_means_with_sem ) mean sem
[1,] 10.053034 0.6426571
[2,] 9.230090 0.6494549
[3,] 9.864098 0.7275161
[4,] 10.133182 0.6748017
[5,] 11.027740 0.4813022
[6,] 10.809995 0.4016863Wie oft liegt der wahre Wert innerhalb von Mittelwert ± Standardfehler?
many_means_with_sem %>%
as_tibble() %>%
mutate( contains_true_value = mean-sem < 10 & mean+sem > 10 ) %>%
summarise( mean(contains_true_value) )# A tibble: 1 × 1
`mean(contains_true_value)`
<dbl>
1 0.687Antwort: 67%. Das war nach der 68-95-99.7-Regel so zu erwarten.
Wenn wir das Interval doppelt so groß machen, erwarten wir Überlapp mit dem wahren Wert in 95% der Fälle:
many_means_with_sem %>%
as_tibble() %>%
mutate( contains_true_value = mean-2*sem < 10 & mean+2*sem > 10 ) %>%
summarise( mean(contains_true_value) )# A tibble: 1 × 1
`mean(contains_true_value)`
<dbl>
1 0.946Das hat funktioniert.
Wir können für einen Mittelwert auf diese Weise ein sog. 95%-Konfidenzintervall (95% confidence interval, 95%-CI) konstruieren:
rnorm( 25, mean=10, sd=3 ) -> x
# Stichproben-Mittelwert:
mean(x) -> mu
# SEM:
sd(x) / sqrt(length(x)) -> sem
sem[1] 0.5288519# zugehöriges 95%-KI
c( mu-2*sem, mu+2*sem )[1] 8.804755 10.920163Kleinliche Anmerkung: Die 68-95-99.7-Regel ist gerundet. Eigentlich muß man für 95% Wahrscheinlichkeit die Standardabweichung nicht mal 2 nehmen, sondern mal 1.96.
Das sieht man, wenn man die qnorm-Funktion fragt, zwischen welchen Werten der Standard-Normalverteilung die mittleren 95% der Fläche (also von 2.5% bis 97.5%) liegen
qnorm( .025 )[1] -1.959964qnorm( .975 )[1] 1.959964kleine Stichproben
Nun das große Aber: Mit einer deutlich kleineren Stichprobe funktioniert es nicht mehr.
Wir versuchen \(n=5\)
replicate( 10000, {
rnorm( 5, mean=10, sd=3 ) -> x
c( mean=mean(x), sem=sd(x)/sqrt(length(x)) )
}) %>% t -> many_means_with_sem
many_means_with_sem %>%
as_tibble() %>%
mutate( contains_true_value = mean-2*sem < 10 & mean+2*sem > 10 ) %>%
summarise( mean(contains_true_value) )# A tibble: 1 × 1
`mean(contains_true_value)`
<dbl>
1 0.886Nur 88% statt 95%.
Der Grund ist das für kleines \(n\) die Schätzung der Standardabweichung zu ungenau ist.
Um das auszugleichen, muss man den SEM mit einer Zahl multiplizieren, die größer ist als 2 (bzw. als 1.96).
Die Student’sche t-Verteilung gibt den korrekten Wert. Wir verwenden qt (Quantile der t-Verteilung) statt qnorm (Quantile der Normalverteilung) und wiederholen die Rechnung von eben:
qt( 0.025, df=4 )[1] -2.776445qt( 0.975, df=4 )[1] 2.776445Die Studentsche t-Verteilung hat einen Parameter, genannt die Anzahl der Freiheitsgrade (degrees of freedom, df). Dies ist stets die Anzahl der Werte minus die Anzahl der Mittelwerte, also hier \(5-1=4\).
(Die Formel, die qt intern verwendet ist etwas kompliziert; siehe Wikipedia.)
Mit dem Faktor 2.78 erreichen wir nun 95% Überdeckungswahrscheinlichkeit
many_means_with_sem %>%
as_tibble() %>%
mutate( contains_true_value = mean-2.78*sem < 10 & mean+2.78*sem > 10 ) %>%
summarise( mean(contains_true_value) )# A tibble: 1 × 1
`mean(contains_true_value)`
<dbl>
1 0.950Die folgende Tabelle zeigt den Faktor, mit dem man den SEM multiplizieren muss, um ein 95%-Konfidenzintervall zu konstruieren.
tibble( n = c(2:10, 15,20, 50, 100, 1000, 10000 ) ) %>%
mutate( f95 = qt( .975, n-1 ) %>% round(2) ) # A tibble: 15 × 2
n f95
<dbl> <dbl>
1 2 12.7
2 3 4.3
3 4 3.18
4 5 2.78
5 6 2.57
6 7 2.45
7 8 2.36
8 9 2.31
9 10 2.26
10 15 2.14
11 20 2.09
12 50 2.01
13 100 1.98
14 1000 1.96
15 10000 1.96Herkunft der t-Verteilung
(für mathematisch Interessierte)
Woher kommt der Wert 2.78 für n=5? Was ist die t-Verteilung?
Wir simulieren 100000 mal folgendes: Ziehe \(n\) Werte aus eine Standard-Normalverteilung, bestimme Mittelwert, Standardabweichung und SEM. Berechne das Verhältnis der Abweichung des Stichprobenmittelwerts vom wahren Wert 0 zum SEM. Wenn die Standardabweichung stets exakt auf 1 geschätzt werden würde, wäre dieses Verhältnis (mit konstant 1 im Nenner) standard-normalverteilt. Da der Nenner aber um 1 fluktuiert, werden die Tails fetter. Die sich ergebende Verteilung ist die t-Verteilung mit \(n-1\) Freiheitsgraden, wie ein Vergleich des Histogramms mit der theoretisch berechneten Dichtekurve (in magenta; die Normalverteilung zum Vergleich in blau)illustriert:
n <- 5
replicate( 100000, {
rnorm( n, mean=0, sd=1 ) -> x
sd(x) / sqrt(n) -> sem
mean(x) / sem
}) -> many_sems
hist( many_sems, 300, xlim=c(-10, 10), freq=FALSE, ylim=c(0,.4) )
xg <- seq( -10, 10, by=.1 )
lines( xg, dnorm( xg ), col="blue" )
lines( xg, dt( xg, n-1 ), col="magenta" )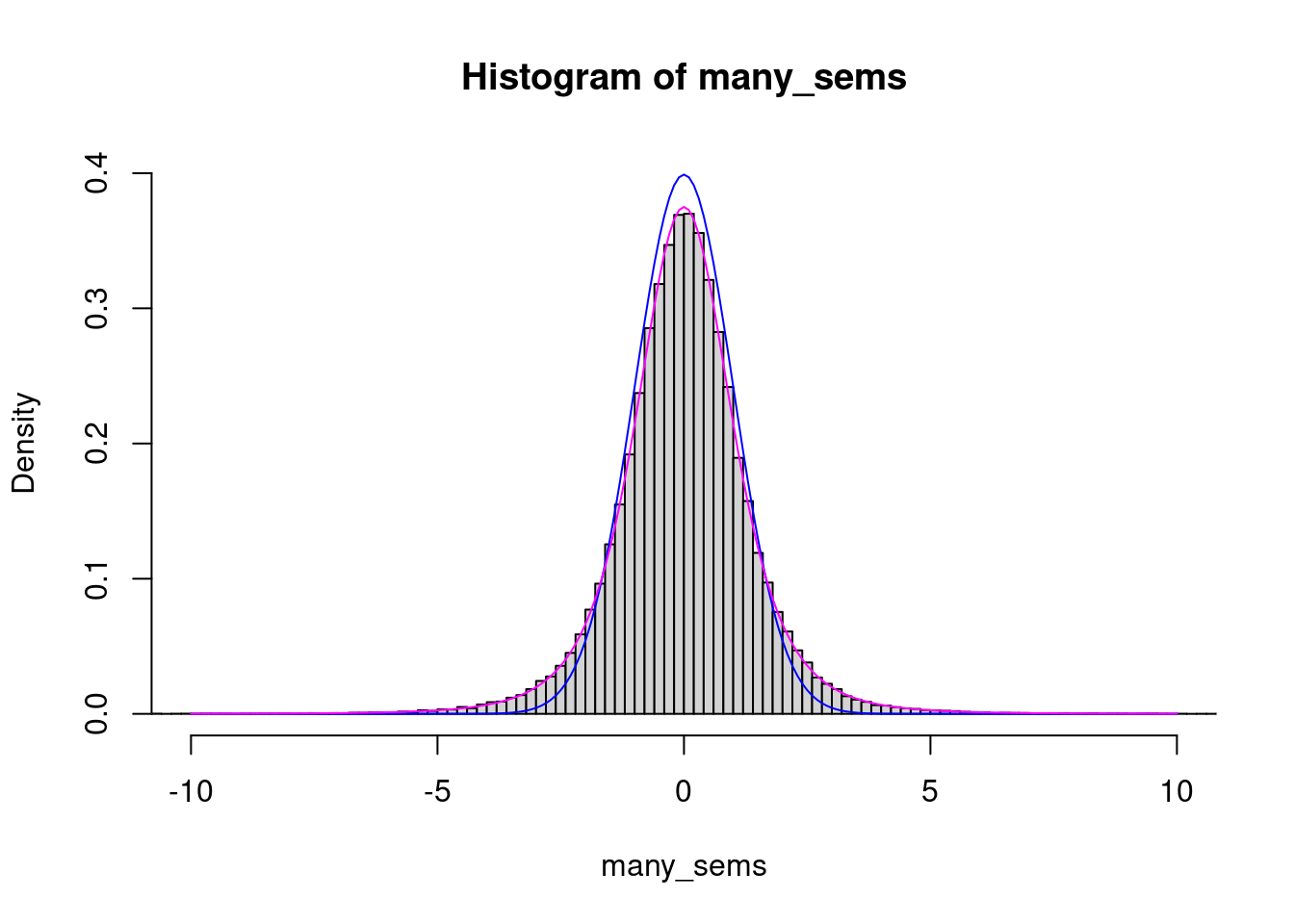
Konfidenzintervalle
Wir fassen zusammen:
Idee
Das Ergebnis einer Messung oder Analyse ist nur von sehr eingeschränktem Nutzen, wenn man nicht weiß, wie genau es ist.
Daher sollte man zu jedem Ergebnis stets ein Konfidenzintervall angeben.
Ein xx%-Konfidenzintervall ist ein Intervall (also eine untere und obere Grenze) um einen Schätzwert, dass einen Bereich angibt, indem der “wahre” Wert der Grundgesamtheit vermutlich liegt. Die Methode, es zu erstellen, ist so konstruiert, dass man mit Wahrscheinlichkeit xx% ein Interval erhält, dass den wahren Wert überdeckt.
Üblicherweise wählt man Konfidenz-Niveau von 95%.
Für einen Stichproben-Mittelwert erhält man das konfidenzintervall wie folgt:
Einfache, aber ungenaue Methode
Sei \(\hat\mu\) der Mittelwert und \(\hat\sigma\) die Standardabweichung der Stichprobe, und \(n\) die Anzahl der Werte in der Stichprobe.
Man berechnet den Standardfehler des Mittelwerts mit der Formel \(\text{SEM}=\hat\sigma/\sqrt{n}\).
Dann nimmt man als 95%-Konfidenzintervall das Intervall von \(\hat\mu-2\hat\sigma\) bis \(\hat\mu+2\hat\sigma\).
Diese Methode sollte man nur verwenden, wenn \(n\) groß ist (min. 20).
(schlechtes) Beispiel:
# Einzelwerte
c( 10.95, 8.21, 8.19, 6.33, 11.09, 12.28, 10.01, 7.14 ) -> x
# Mittelwert
mean(x) -> mymean
mymean[1] 9.275#SEM
sd(x)/sqrt(length(x)) -> sem
# KI
c( mymean - 2*sem, mymean + 2*sem )[1] 7.781854 10.768146(kein gutes Beispiel, da \(n\) zu klein ist für die ungenaue Methode)
Genauere Methode
Wenn \(n\) klein ist, muss man in der Formel für die Grenzen des Konfidenz-Intervalls die Zahl 2 durch eine Zahl ersetzen, die man aus der t-Verteilung erhält:
qt( .975, n-1 )Für großes \(n\) ergibt diese Formel in etwa den Wert 2 (genauer: 1.96).
Das .975 ist dabei die obere Quantilgrenze, die man erhält als Mitte zwischen 95% und 100%.
Also: Konfidenzintervall von \(\hat\mu-q\hat\sigma\) bis \(\hat\mu+q\hat\sigma\), wobei \(q\) der Wert des 97.5%-Quantils der \(t\)-Verteilung mit \(n-1\) Freiheitsgraden ist.
Beispiel (mit den Variablen von oben):
qt( .975, length(x)-1 ) -> q
# KI
c( mymean - q*sem, mymean + q*sem )[1] 7.509635 11.040365Bequeme Methode
Die t.test-Funktion von R kann nicht nur t-Tests durchführen, sondern auch KIs berechnen:
t.test(x)$conf.int[1] 7.509635 11.040365
attr(,"conf.level")
[1] 0.95Wir erhalten dasselbe Ergebnis wie zuvor.
Vergleich von Mittelwerten
Beispiel
Wir betrachten das folgende Beispiel als Prototyp für die Aufgaben, die wir hier behandeln möchten:
Forscher möchten heraus finden, ob eine gewisse Substanz zu Gewichtserhöhung führt (z.B., weil sie den Appetit stimuliert oder die Insulinantwort beeinflusst). Dazu werden Versuchstiere (Mäuse) in zwei Gruppen aufgeteilt. Einer Gruppe, der “treatment group” (behandelte Gruppe) wird die Substanz ins Futter gemischt, der anderen Gruppe, genannt “control group” (Vergleichsgruppe) hingegen nicht. Anfangs sind alle Mäuse in etwa gleich schwer. Nach drei Wochen werden alle Tiere gewogen. Wir möchten wissen, ob der Erwartungswert des Gewichts in der behandelten Gruppe (“Gruppe T” für “treatment”) anders ist als der Erwartungswert in der Vergleichgruppe (“Gruppe C” für “control”).
So wie im folgenden könnten die Daten aussehen:
set.seed( 1324996 )
bind_rows(
tibble( weight = rnorm( n=20, mean=22, sd=4 ), group = "C" ),
tibble( weight = rnorm( n=20, mean=26, sd=4 ), group = "T" ) ) -> weight_data
beeswarm::beeswarm( weight ~ group, weight_data )
Anmerkungen:
Das Gewicht einer Maus hängt nicht nur davon ab, welche der beiden Futtermischungen sie erhält, sondern auch von vielen anderen Faktoren, die wir nicht kennen und/oder nicht beeinflussen können.
Unsere Frage bezieht sich auf den Erwartungswert, also den Mittelwert, den man erhielte, wenn man das Experiment mit “unendlich” vielen Mäusen durchführte, so dass sich alle anderen Einflüssen in beiden Gruppen zum gleichen Wert “heraus mitteln”.
Der Umfang dieser anderen Einflüsse wird durch die Standardabweichung (Varianz) in der Grundgesamtheit beschrieben.
Grundsätzliche Idee:
Wir bestimmen in beiden Gruppen den Mittelwert und das zugehörige Konfidenzintervall. Daraus können wir die Differenz der Mittelwerte bestimmen, sowie ein Konfidenzintervall für die Differenz.
Wenn das 95%-Konfidenzintervall der Differenz die Null nicht überdeckt, können wir “mit 95% Konfidenz” sagen, dass das Futter (bzw. dir zugemischte Substanz) einen Einfluss auf das Gewicht hat.
Wenn es hingegen die Null überdeckt, können wir mit 95% Konfidenz sagen: Die Substanz hat entweder gar keinen Effekt, oder der Effekt ist nicht oder kaum größer als das Konfidenzintervall breit ist.
Wichtig: Wenn das KI die Null überdeckt und sehr breit ist, können wir gar nichts folgern.
Zu folgern, die Substanz habe keinen Effekt, weil das Testergebnis “nicht signifikant” war (d.h.: das KI der Differenz hat die Null überdeckt), ist falsch!
Rechnung für Beispiel
vorab: MIttelwerte der Gruppen
Wir berechnen zunächst die KIs der Mittelwerte der beiden Gruppen:
weight_data %>%
group_by( group ) %>%
summarise( broom::tidy( t.test( weight ) ) ) %>%
select( group, mean=estimate, conf.low, conf.high ) -> weight_data_means
weight_data_means# A tibble: 2 × 4
group mean conf.low conf.high
<chr> <dbl> <dbl> <dbl>
1 C 21.1 19.5 22.8
2 T 26.3 24.4 28.3Zur Erinnerung: Hier wird (noch) kein t-Test durchgeführt. Wir “misbrauchen” die t.test-Funktion lediglich, um das KI zu bekommen.
Graphische Darstellung:
ggplot( NULL ) +
geom_errorbar( aes( x=group, ymin=conf.low, ymax=conf.high ), data=weight_data_means, width=.4, col="magenta" ) +
geom_beeswarm( aes( x=group, y=weight ), data=weight_data ) 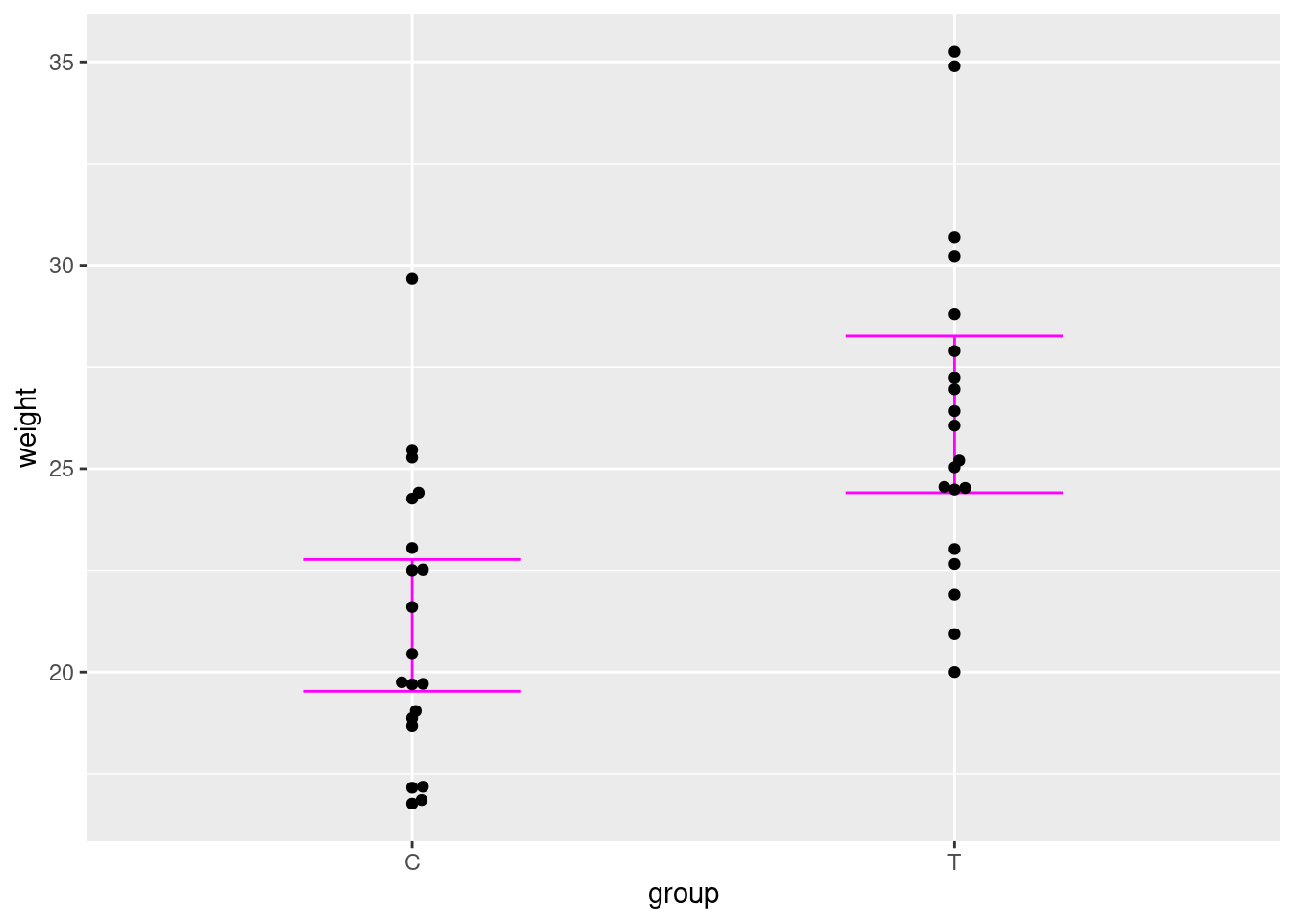
Die KIs überlappen sich nicht. Wir können also mit 95% Konfidenz sagen, dass die Substanz eine Gewichtszunahme bewirkt.
t-Test
Statt die KIs der Gruppen-Mittelwerte zu vergleichen, betrachtet man besser direkt das KI der Differenz der Mittelwerte.
Die t.test-Funktion berechnet es für uns:
t.test( weight ~ group, weight_data )
Welch Two Sample t-test
data: weight by group
t = -4.313, df = 36.897, p-value = 0.0001154
alternative hypothesis: true difference in means between group C and group T is not equal to 0
95 percent confidence interval:
-7.630353 -2.752274
sample estimates:
mean in group C mean in group T
21.14547 26.33678 Die Differenz “Erwartungswert für C minus Erwartungswert für T” liegt also mit 95% Konfidenz im zwischen -7.63 und -2.75
Vergleich der KIs
Die Breite des KIs der Differenz ist kleiner als die Summe der Breiten der KIs der beiden Gruppen-Mittelwerte.Daher kann es vorkommen, dass das KI der Differenz die 0 nicht überlappt (“Differenz ist statistisch signifikant”) obwohl die KIs der Einzelwerte miteinander überlappen.
Grund: Die Summe oder Differenz zweier Werte hat weniger Unsicherheit als die Einzelwerte, weil sich Fluktationen ausgleichen (ausmitteln).
(Mathematisch: Die Summe oder Differenz zweier Werte mit Standardfehlern \(u_1\) und \(u_2\) hat Standardfehler \(u\) mit \(u^2=u_1^2+u_2^2\). Man sagt: Standardfehler addieren sie “pythagoräisch”, also, wie im Satz des Pythagoras.)
Wenn gewünscht, schätzt die t.test-Funktion die Standardabweichung nicht für jede Gruppe getrennt, sondern für beide Gruppen gemeinsam (sog. “gepoolte Standardabweichung”). Da die Daten aus beiden Gruppen zusammen genommen werden, ist die Anzahl der Freiheitsgrade größer und der oben beschriebene Faktor \(q\) kleiner. Das ist nur zulässig, wenn angenommen werden darf, dass die Standardabweichung in den Grundgesamtheiten der beiden Gruppen gleich ist. Das macht das KI noch etwas enger.
Bei unserem Beispiel macht es aber kaum einen Unterschied:
t.test( weight ~ group, weight_data, var.equal=TRUE )
Two Sample t-test
data: weight by group
t = -4.313, df = 38, p-value = 0.0001104
alternative hypothesis: true difference in means between group C and group T is not equal to 0
95 percent confidence interval:
-7.627959 -2.754668
sample estimates:
mean in group C mean in group T
21.14547 26.33678 In der Literatur wird der t-Test mit var.equal=TRUE oft als der ursprüngliche t-Test von Student bezeichnet, und die Variante mit var.equal=FALSE (der Default in R) als Welch’s t-Test.
p-Wert
In unserem Beispiel liegt die Null weit außerhalb des 95%-KI der Mittelwert-Differenz. Ist das auch noch der Fall, wenn wir für die Differenz ein 99,9%-KI berechnen?
t.test( weight ~ group, weight_data, conf.level=.999 )
Welch Two Sample t-test
data: weight by group
t = -4.313, df = 36.897, p-value = 0.0001154
alternative hypothesis: true difference in means between group C and group T is not equal to 0
99.9 percent confidence interval:
-9.4937610 -0.8888667
sample estimates:
mean in group C mean in group T
21.14547 26.33678 Ja. Die Untergrenze des KI ist aber näher an 0 heran gerückt
Bei welchem Konfidenz-Niveau erreicht das KI die Null? Diese Frage beantwortet die t-Test-Funktion mit Angabe des sog. “p-Werts”, hier 0.00012. Bei einem Konfidenz-Niveau von 99.988% wird die Null vom Diffferenz-KI gerade berührt:
t.test( weight ~ group, weight_data, conf.level=1-0.0001154 )
Welch Two Sample t-test
data: weight by group
t = -4.313, df = 36.897, p-value = 0.0001154
alternative hypothesis: true difference in means between group C and group T is not equal to 0
99.98846 percent confidence interval:
-1.038253e+01 -9.765673e-05
sample estimates:
mean in group C mean in group T
21.14547 26.33678 Definition 1 des p-Werts: (Wir werden später noch eine weiter, äquivalente, Defintion kennen lernen)
Der p-Wert ist ein Wert, den ein statistischer Test berechnet. Ein p-Wert \(p\) bedeutet, dass die Daten Evidenz bieten, um den vermuteten Effekt mit Konfidenz bis zu \(1-p\) als signifikant anzusehen, d.h., auszuschließen, dass der Effekt 0 ist.
Bei unserem Beispiel ist klar, was gemeint ist mit “der Effekt ist 0”: nämlich dass die Differenz der Gruppen-Erwartungswerte 0 ist.
Im Allgemeinen muss man beschreiben, was man meint; diese Beschreibung nennt man die Null-Hypothese.
Die allgemeine Definition des p-Werts lautet:
Der p-Wert ist die Wahrscheinlichkeit, dass das beobachtete Ergebnis, oder ein noch extremeres, eintritt, wenn die Null-Hypothese abgenommen wird.
Was bedeutet “oder noch extremer”?
Die t-Statistik
Welcher der beiden folgenden Fälle ist “extremer”?
set.seed( 1324 )
bind_rows(
tibble( group="C", experiment="A", value=rnorm( 20, 20, 4 ) ),
tibble( group="T", experiment="A", value=rnorm( 20, 27, 4 ) ),
tibble( group="C", experiment="B", value=rnorm( 20, 20, .5 ) ),
tibble( group="T", experiment="B", value=rnorm( 20, 23, .5 ) ) ) -> data2exp
data2exp %>%
ggplot +
geom_beeswarm( aes( x=group, y=value ), cex=2.2 ) +
facet_grid( cols=vars(experiment) )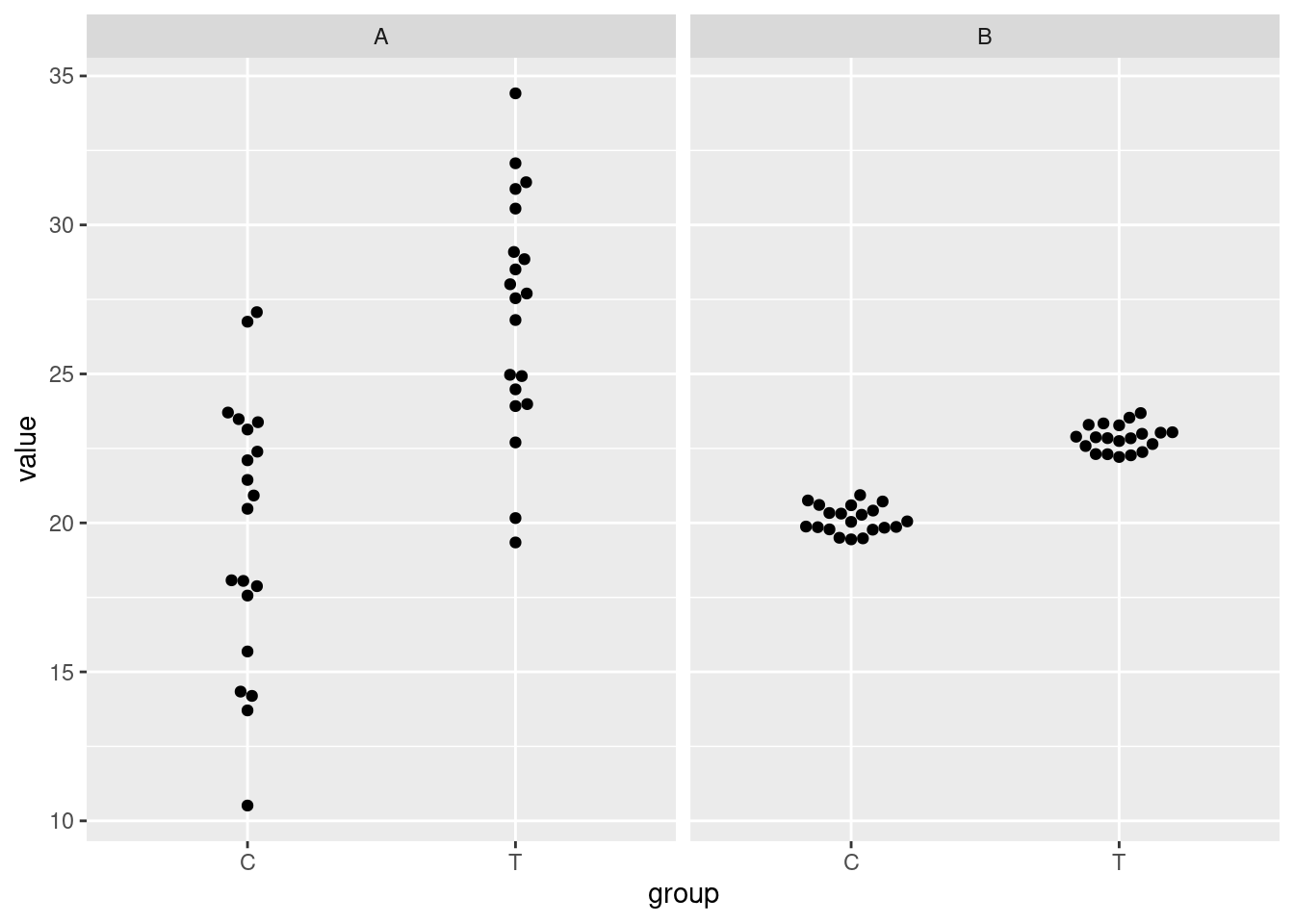
Die Differenz der Mittelwerte ist links viel größer als rechts, aber rechts ist das Ergebnis “klarer”.
Lösung: Berechne die Differenz und ihren Standardfehler und betrachte ihr Verhältnis:
\[t\text{-Statistik} = \frac{\text{Differenz der Mittelwerte}}{\text{Standardfehler der Differenz}}\] Die Verteilung dieses Werts ist die Studentsche \(t\)-Verteilung mit \(n-2\) Freiheitsgraden (wobei \(n\) die Anzahl der Werte in beiden Gruppen zusammen ist). Dieser Wert liegt im t-Test der Berechnung von Differenz-KI und p-Wert zugrunde.
Die t-Test-Funktion gibt uns alle diese Werte aus:
data2exp %>%
group_by( experiment ) %>%
summarise( broom::tidy( t.test( value ~ group, var.equal=TRUE ) ) )# A tibble: 2 × 11
experiment estimate estimate1 estimate2 statistic p.value parameter conf.low
<chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 A -7.29 19.7 27.0 -5.43 3.49e- 6 38 -10.0
2 B -2.73 20.1 22.9 -19.6 1.81e-21 38 -3.01
# ℹ 3 more variables: conf.high <dbl>, method <chr>, alternative <chr>estimate1undestimate2sind die Gruppen-Mittelwerteestimateist die Differenz der Mittelwertestatisticist die t-Statistikparameterist die Anzahl der Freiheitsgrade für die t-Verteilungp.valueist die Wahrscheinlichkeit, den genannten t-Wert, oder einen im Betrag größeren, zu erhaltenconf.lowund.conf.highsind die Grenzen des 95%-Konfidenzintervalls der Differenzalternative=two-sidedgibt an, dass bei der p-Wert-Berechnung angenommen wurde, dass die Differenz in beide Richtungen extremer sein könnte
Nur für Interessierte: Im folgenden berechnen wir diese Werte für Experiment A per Hand.
data2exp %>%
filter( experiment=="A" ) %>%
group_by( group ) %>%
mutate( group_mean = mean(value) ) %>%
ungroup %>%
mutate( residuals = value - group_mean ) %>%
summarise( sum_of_squares = sum( residuals^2 ), n=n() ) %>%
mutate( pooled_variance = sum_of_squares / (n-2) ) %>%
mutate( pooled_sd = sqrt( pooled_variance ) ) %>%
pull(pooled_sd) -> pooled_sd
data2exp %>%
filter( experiment=="A" ) %>%
group_by( group ) %>%
summarise(
group_mean = mean(value),
group_mean_se = pooled_sd / sqrt( n() ),
n=n() ) %>%
summarise(
mean_diff = diff( group_mean ),
mean_diff_se = sqrt( sum( group_mean_se^2 ) ),
n = sum(n) ) %>%
mutate( t = mean_diff / mean_diff_se ) %>%
mutate( p = 2* ( 1-pt( t, n-2 ) ) )# A tibble: 1 × 5
mean_diff mean_diff_se n t p
<dbl> <dbl> <int> <dbl> <dbl>
1 7.29 1.34 40 5.43 0.00000349Statistische Power
Wir wiederholen das simulierte Experiment von oben, diesmal mit Base-R statt Tidyverse:
ctrl <- rnorm( n=20, mean=22, sd=4 )
treat <- rnorm( n=20, mean=26, sd=4 )
t.test( ctrl, treat )
Welch Two Sample t-test
data: ctrl and treat
t = -3.8275, df = 37.413, p-value = 0.0004771
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-7.392805 -2.276194
sample estimates:
mean of x mean of y
21.66853 26.50303 WIr können dies 1000 mal durchführen und fragen, wie oft der p-Wert unter 0.05 war:
replicate( 10000, {
ctrl <- rnorm( n=20, mean=22, sd=4 )
treat <- rnorm( n=20, mean=25, sd=4 )
t.test( ctrl, treat )$p.value } ) -> many_pvals
mean( many_pvals < .05 )[1] 0.6392Wir können dieses Ergebnis wie folgt beschreiben:
Wenn die (uns unbekannten, wahren) Parameter des Experiments wie folgt sind:
- Die Standardabweichung des Gewichts von Mäusen, die dasselbe Futter erhalten, ist 4 g.
- Der Effekt der zugemischten Substanz ist eine Gewichtszunahme von 3 g (von 22 g auf 25 g)
und wenn wir für beide Gruppen je 20 Mäuse verwenden,
und wie ein Konfidenzniveau von 95% (also einen p-Wert unter 5%) erfordern,
dann ist die Wahrscheinlichkeit, dass wir belegen können, dass die Substanz das Gewicht beeinflusst, 64%.
Rechnen statt Simulieren
Die 10000 Simulation brauchen recht lange. Zum Glück kann man die Wahrscheinlichkeit auch mit einer Formel berechnen. Die Funktion power.t.test liefert dasselbe Ergebnis wie die Simulation eben, aber viel schneller:
power.t.test( n=20, delta=3, sd=4 )
Two-sample t test power calculation
n = 20
delta = 3
sd = 4
sig.level = 0.05
power = 0.6373921
alternative = two.sided
NOTE: n is number in *each* groupDer folgende Code ruft diese Funktion für eine Vielzahl vom Kombinationen von Werten auf:
expand_grid( diff=seq( 0, 6, by=.1 ), n=c(5, 10, 20, 50, 200, 1000 ) ) %>%
rowwise() %>%
mutate( power = power.t.test( n=n, delta=diff, sd=4, sig.level = 0.01 )$power ) %>%
ggplot( aes( x=diff, y=power, col=factor(n) ) ) +
geom_line() +
labs(
x = "difference between means (true effect size)",
y = "statistical power (i.e., prob to get p<.05)",
col = "n",
title = "Power of a t-test",
subtitle = "(for within-group SD = 4)")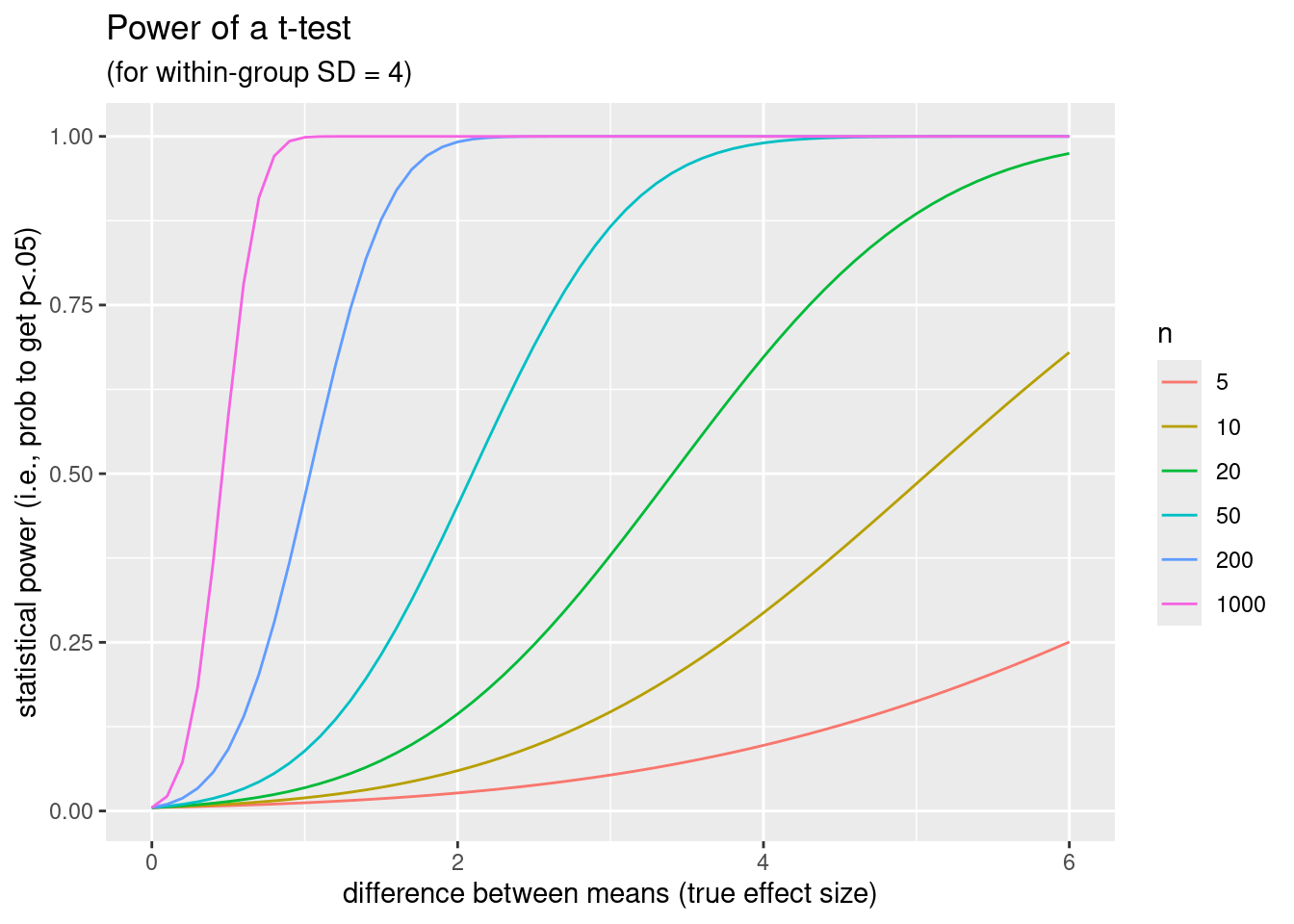
Dieser Plot zeigt uns die statistische Power eines t-Tests, wenn die wahre “within-group standard deviation” 4 beträgt, in Abhängigkeit von der wahren Differenz der Mittelwerte (x-Achse) und der Anzahl Mäuse pro Gruppe (Farbe).
Dieser Plot passt zu unserem Beispiel; besser wäre es aber, die Differenz (x-Achse) in Einheiten der Standardabweichung darzustellen:
expand_grid( diff=10^seq( -2, 1, by=.01 ), n=c(2, 3, 5, 10, 30, 100, 300, 1000 ) ) %>%
rowwise() %>%
mutate( power = power.t.test( n=n, delta=diff, sd=1 )$power ) %>%
ggplot( aes( x=diff, y=power, col=fct_rev(factor(n)) ) ) +
geom_line() +
scale_x_log10() +
labs(
x = "true effect size in units of within-group SD",
y = "statistical power at 95% confidence level",
col = "n",
title = "Power of a t-test" )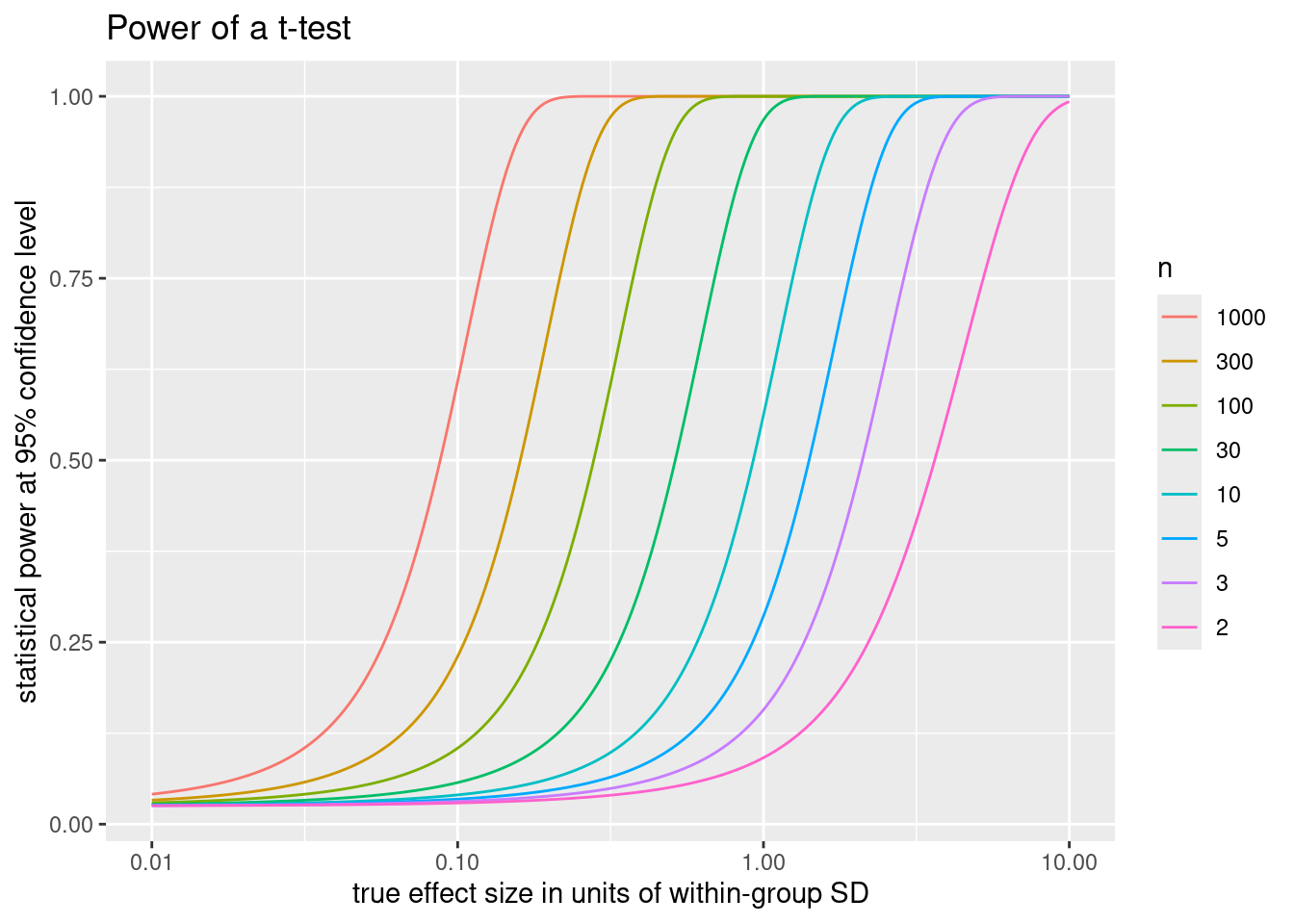
False positives
Beachten Sie die linke untere Ecke des Plots:
Die Wahrscheinlichkeit, dass man ein positives Ergebnis (p<0.05) erhält, obwohl der wahre Effekt 0 ist, beträgt 0.05. Das ist genau, was man nach Definition des p-Werts erwartet.
Das bedeutet aber nicht, dass die Wahrscheinlichkeit eines False-Positives 5% und die Wahrscheinlichkeit eines true positives 95% wäre – denn die Zahl gilt ja nur, wenn die wahre Effektgröße 0 wäre, was man ja nicht weiß.
Permutations-Tests
Permutationen
Unter einer Permutation versteht man eine Umordnung einer Liste von Elementen, d.h., die permutierte Liste enthält dieselben Element, aber in einer anderen Reihenfolge.
Beispiel: Wir haben diesen Vektor:
x <- c( "A", "B", "B", "D", "A", "F", "G", "H" )Mit der Funktion sample können wir eine zufällige Permutation erhalten:
sample(x)[1] "G" "F" "D" "A" "B" "H" "A" "B"sample(x)[1] "A" "H" "G" "F" "D" "B" "B" "A"sample(x)[1] "H" "A" "B" "G" "B" "F" "D" "A"Beispiel für Test
Permutations-Tests sind ein allgemeines Konzept, dass man oft anwenden, wenn ein spezieller, auf die Situation passender Test, nicht zur Verfügungs steht. Wir demonstrieren die Idee hier am Beispiel des Vergleichs zweier Mittelwerte – auch wenn dies eine Situtation ist, wo ein speziell auf die Aufgabe passender Test, nämlich der t-Test, geeigneter wäre.
Beispieldaten: 10-jährige Probanden in NHANES. Vegleich Körpergröße Mädchen und Jungen:
read_csv( "data_on_git/nhanes.csv" ) %>%
filter( age == 10, !is.na(height) ) -> nhanes10Rows: 8704 Columns: 6
── Column specification ────────────────────────────────────────────────────────
Delimiter: ","
chr (2): gender, ethnicity
dbl (4): subjectId, age, height, weight
ℹ Use `spec()` to retrieve the full column specification for this data.
ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message.head( nhanes10 )# A tibble: 6 × 6
subjectId gender age height weight ethnicity
<dbl> <chr> <dbl> <dbl> <dbl> <chr>
1 93744 female 10 155. 50.8 NH White
2 93753 female 10 151. 56.3 NH White
3 93779 female 10 139. 31.7 Other/Mixed
4 93876 male 10 151. 56.6 Mexican
5 93896 male 10 148. 65.8 NH White
6 93897 female 10 149 58.7 NH White Natürlich ist das geeignete Mittel für diese Aufgabe der t-Test:
t.test( height ~ gender, nhanes10 )
Welch Two Sample t-test
data: height by gender
t = 1.8163, df = 180.98, p-value = 0.07098
alternative hypothesis: true difference in means between group female and group male is not equal to 0
95 percent confidence interval:
-0.1541084 3.7235707
sample estimates:
mean in group female mean in group male
143.8914 142.1067 Wir betrachten nun dennoch den Permutationstest als Alternative.
Nullhypothese: Das Geschlecht hat bei 10jährigen keinen Einfluss auf die Körpergröße. Der Unterschied zwischen den Mittelwerten von Jungen und Mädchen entsteht nur dadurch, dass man nie zweimal denselben Mittelwert erhält, wenn man Werte auf zwei Gruppen aufteilt.
Teststrategie: Wir berechnen die Differenz der Mittelwerte nach einer zufälligen Durchmischung der Zuordnung der Werte zu den beiden Geschlechtern.
Hier eine Permutation der Spalte gender:
nhanes10 %>%
mutate( gender_perm = sample(gender) )# A tibble: 183 × 7
subjectId gender age height weight ethnicity gender_perm
<dbl> <chr> <dbl> <dbl> <dbl> <chr> <chr>
1 93744 female 10 155. 50.8 NH White male
2 93753 female 10 151. 56.3 NH White male
3 93779 female 10 139. 31.7 Other/Mixed male
4 93876 male 10 151. 56.6 Mexican female
5 93896 male 10 148. 65.8 NH White female
6 93897 female 10 149 58.7 NH White female
7 93904 male 10 154. 68.2 Other/Mixed male
8 94024 male 10 138. 34.3 Other Hispanic male
9 94032 male 10 141. 48.7 Other/Mixed male
10 94136 male 10 140. 31.4 Other Hispanic female
# ℹ 173 more rowsDifferenz der Mittelwerte mit korrekter Geschlechter-Zuordnung:
nhanes10 %>%
group_by( gender ) %>%
summarise( mean_height = mean(height) ) %>%
pull( mean_height )[1] 143.8914 142.1067Dasselbe in Base-R (weil schneller als Tidyverse):
tapply( nhanes10$height, nhanes10$gender, mean ) -> means
means female male
143.8914 142.1067 Differenz:
means["male"] - means["female"] male
-1.784731 Dasselbe, aber mit permutierter Geschlechter-Zuordnung:
tapply( nhanes10$height, sample(nhanes10$gender), mean ) -> means
means["male"] - means["female"] male
0.4125806 Wir führen den vorstehenden Code-Chunk sehr oft aus:
set.seed( 13245768 )
replicate( 10000, {
tapply( nhanes10$height, sample(nhanes10$gender), mean ) -> means
means["male"] - means["female"]
} ) -> many_diffs
str( many_diffs ) Named num [1:10000] 0.3361 0.5088 0.4432 0.0999 -0.2892 ...
- attr(*, "names")= chr [1:10000] "male" "male" "male" "male" ...Hier ist ein Histogramm der “Permutations-Null-Verteilung” der Differenzen
hist( many_diffs )
abline( v = -1.784731, col="red" )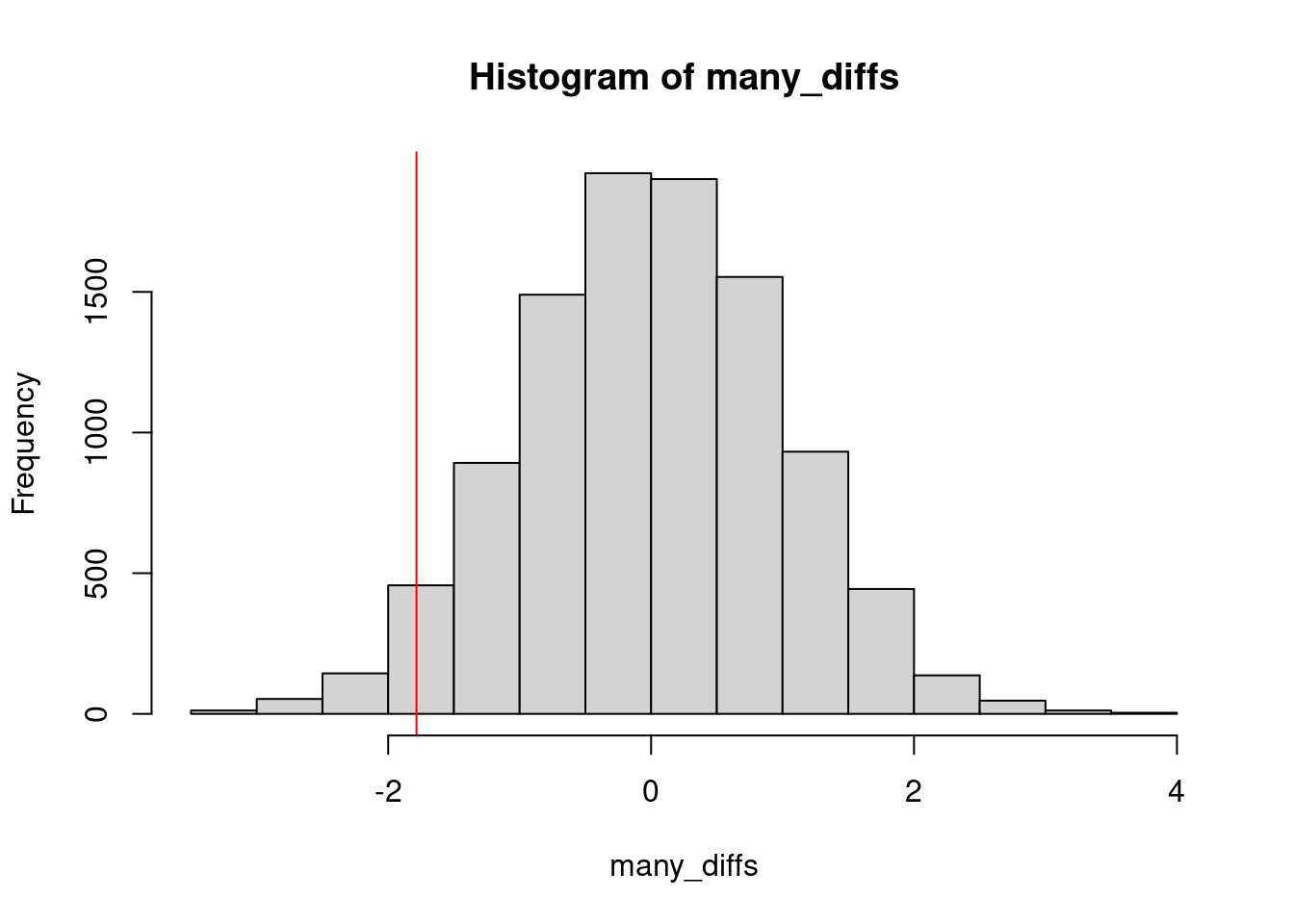
Die rote Linie markiert den beobachteten Wert der Differenz (s.o.).
Welcher Anteil der Permutations-Null-Werte ist weiter von 0 entfernt (also, im Betrag größer) als die beobachtete Differenz?
sum( abs(many_diffs) > 1.784731 ) [1] 714(Die Funktion abs berechnet den Absolutbetrag (absolute value), d.h., entfernt negative Vorzeichen.)
714 von 10000 Werten, also 7%.
Unser Permutations p-Wert beträgt somit 715/10001 = 0.071.
(Man addiert 1 zu Zähler und Nenner, damit auch bei Zähler 0 der p-Wert die Anzahl der durchgeführten Permutationen widerspiegelt.)
Der p-Wert liegt recht nahe am p-Wert des t-Tests.
Natürlich ist ein Permutations-p-Wert bei jeder Berechnung leicht anders. Wenn man aber genügend Permutationen durchführt, ändert er sich nur leicht.
gepaarte Tests
Beispiel: Eine Landwirtschaftliche Versuchsanstalt verfügt über eine größere Zahl von Ackern, die sich alle in der Bodenbeschaffenheit unterscheiden. Ein neuer Dünger für Weizen soll getestet werden.
Szenario A: Auf allen Feldern wird Weizen gesäht. Jedes Feld wird zufällig einer von zwei Gruppen (T und C) zugewiesen. Die T-Felder erhalten den Dünger, die C-Felder nicht.
Szenario B: Jedes Feld wird in zwei Hälften aufgeteilt (“split-plot design”). Eine Hälfte erhält den Dünger, die andere nicht.
Simulation von Szenario A
Wir haben 20 Felder. Der Ertrag (“yield”) ohne den Dünger variiertet von Feld zu Feld. Ebenso variiert der Effekt, den der Dünger für das jeweilige Feld hat bzw. hätte.
set.seed( 1234 )
tibble( plot = 1:20 ) %>%
mutate(
yield_without_fertilizer = rnorm( n(), 100, 30 ),
fertilizer_effect = rnorm( n(), 5, 4 ) ) -> plots0
plots0# A tibble: 20 × 3
plot yield_without_fertilizer fertilizer_effect
<int> <dbl> <dbl>
1 1 63.8 5.54
2 2 108. 3.04
3 3 133. 3.24
4 4 29.6 6.84
5 5 113. 2.23
6 6 115. -0.793
7 7 82.8 7.30
8 8 83.6 0.905
9 9 83.1 4.94
10 10 73.3 1.26
11 11 85.7 9.41
12 12 70.0 3.10
13 13 76.7 2.16
14 14 102. 2.99
15 15 129. -1.52
16 16 96.7 0.330
17 17 84.7 -3.72
18 18 72.7 -0.364
19 19 74.9 3.82
20 20 172. 3.14 Nun weisen wir die Felder den zwei Gruppen zu und simulieren die Ernte, indem wir den Dünger-Effekt bei den gedüngten Feldern hinzufügen:
plots0 %>%
mutate( group = sample( rep( c( "C", "T" ), each=10 ) ) ) %>%
mutate( yield = yield_without_fertilizer + ifelse( group=="T", fertilizer_effect, 0 ) ) -> plots
plots# A tibble: 20 × 5
plot yield_without_fertilizer fertilizer_effect group yield
<int> <dbl> <dbl> <chr> <dbl>
1 1 63.8 5.54 C 63.8
2 2 108. 3.04 T 111.
3 3 133. 3.24 C 133.
4 4 29.6 6.84 C 29.6
5 5 113. 2.23 C 113.
6 6 115. -0.793 C 115.
7 7 82.8 7.30 C 82.8
8 8 83.6 0.905 T 84.5
9 9 83.1 4.94 T 88.0
10 10 73.3 1.26 T 74.6
11 11 85.7 9.41 T 95.1
12 12 70.0 3.10 C 70.0
13 13 76.7 2.16 C 76.7
14 14 102. 2.99 T 105.
15 15 129. -1.52 T 127.
16 16 96.7 0.330 C 96.7
17 17 84.7 -3.72 T 80.9
18 18 72.7 -0.364 C 72.7
19 19 74.9 3.82 T 78.7
20 20 172. 3.14 T 176. Diese Werte sieht als der Versuchsleiter:
plots %>%
ggplot + geom_beeswarm( aes( x=group, y=yield ), cex=2.5 )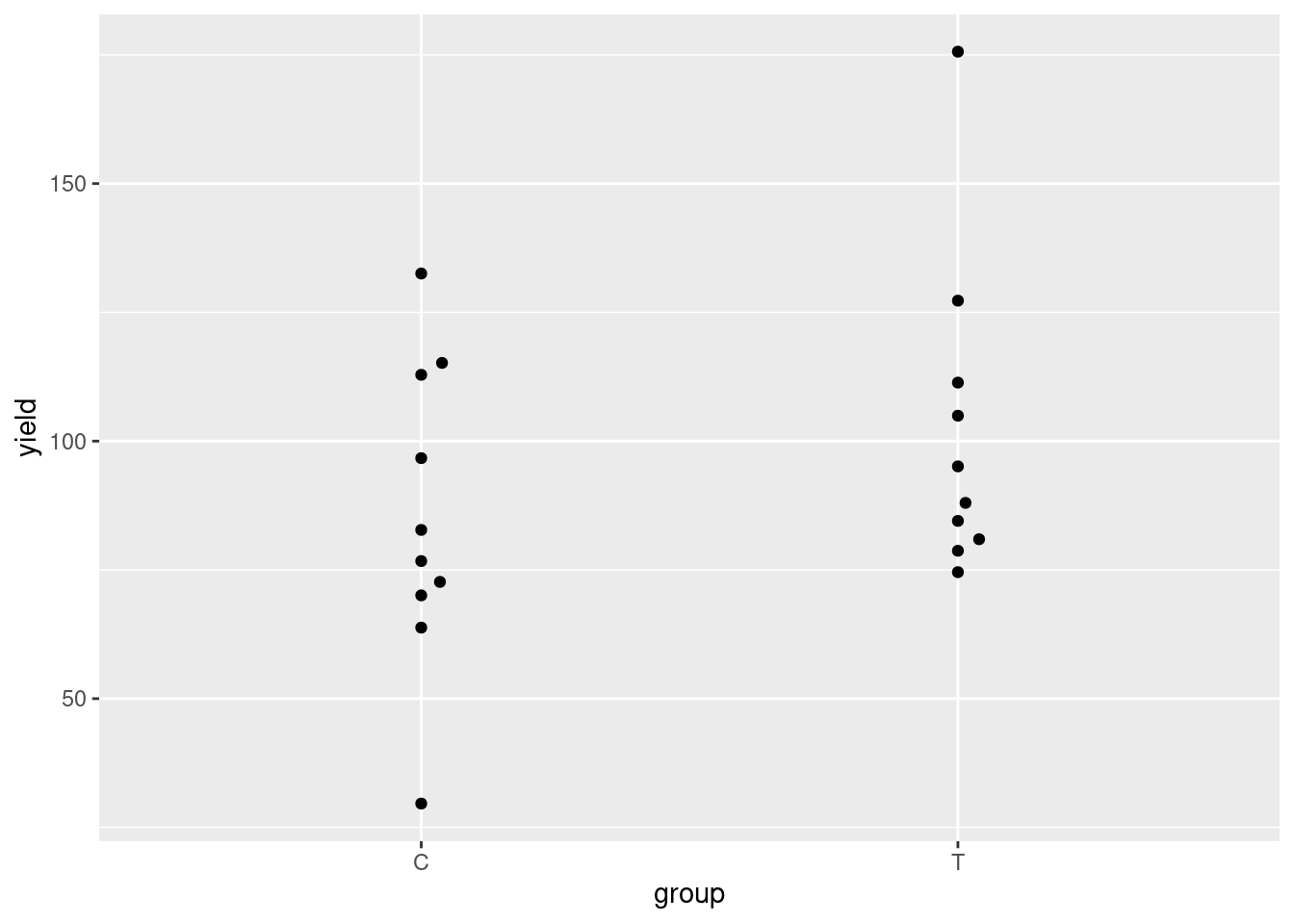
Der t-Test gibt kein klares Bild:
t.test( yield ~ group, plots )
Welch Two Sample t-test
data: yield by group
t = -1.2419, df = 17.99, p-value = 0.2302
alternative hypothesis: true difference in means between group C and group T is not equal to 0
95 percent confidence interval:
-45.24997 11.62859
sample estimates:
mean in group C mean in group T
85.28799 102.09868 Simulation von Szenario B
Wir haben nun nur 10 Felder, die wir aber in 2 Hälften teilen, die wir “C” und “T” nennen:
plots0 %>% head(10) %>%
mutate(
yield_C = yield_without_fertilizer,
yield_T = yield_without_fertilizer + fertilizer_effect
) %>%
select( plot, yield_C, yield_T ) -> plotsB
plotsB# A tibble: 10 × 3
plot yield_C yield_T
<int> <dbl> <dbl>
1 1 63.8 69.3
2 2 108. 111.
3 3 133. 136.
4 4 29.6 36.5
5 5 113. 115.
6 6 115. 114.
7 7 82.8 90.1
8 8 83.6 84.5
9 9 83.1 88.0
10 10 73.3 74.6plotsB %>%
pivot_longer( c( "yield_C", "yield_T" ), names_to = "half", values_to="yield" ) %>%
mutate( half = str_remove( half, "yield_" ) ) -> plotsB_long
plotsB_long %>%
ggplot( aes( x=half, y=yield ) ) +
geom_point() + geom_line( aes( group=plot ) )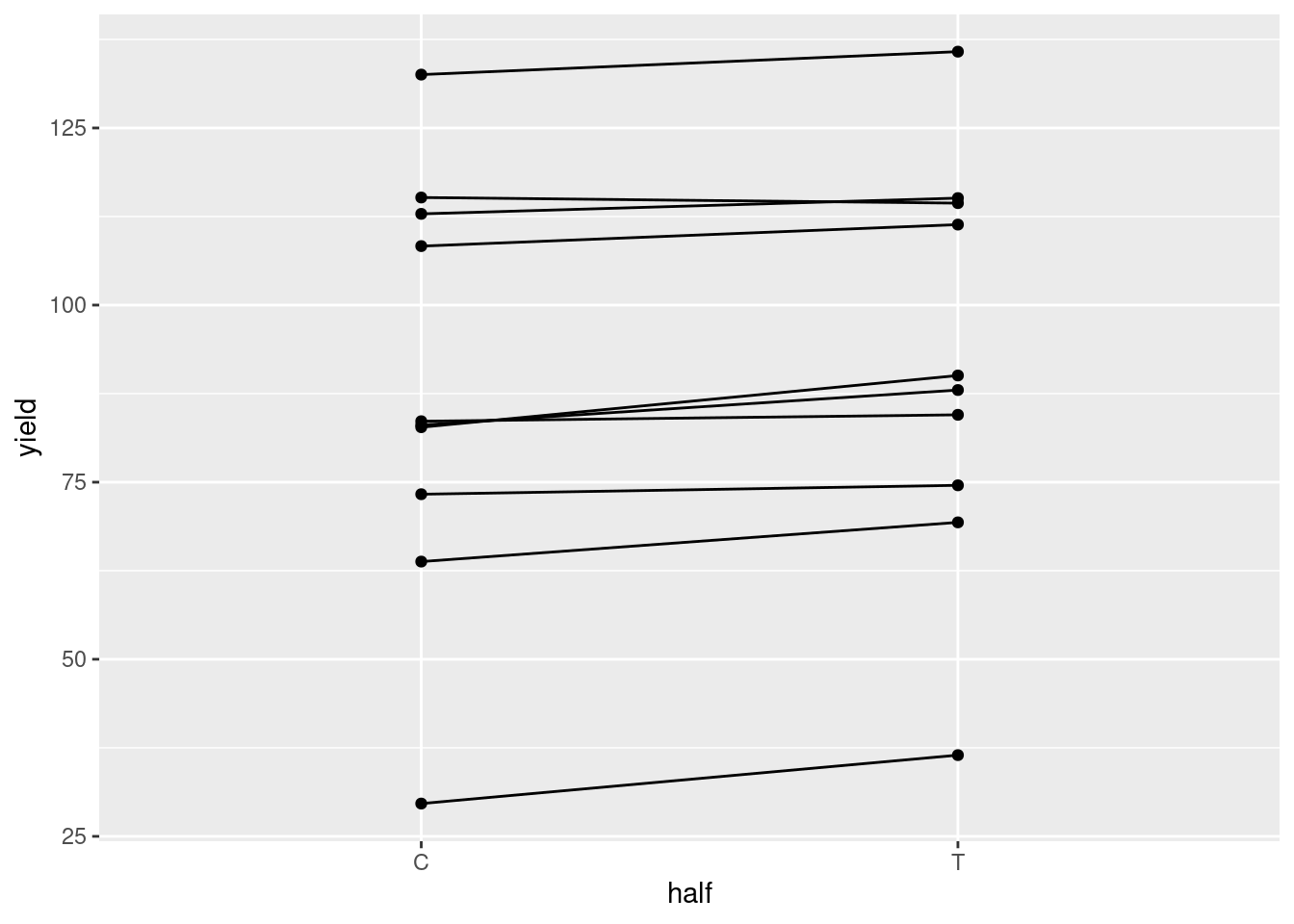
Wenn wir einen normalen t-Test machen, der die beiden Gruppen vergleicht, haben wir nichts gewonnen:
t.test( yield ~ half, plotsB_long )
Welch Two Sample t-test
data: yield by half
t = -0.26416, df = 17.96, p-value = 0.7947
alternative hypothesis: true difference in means between group C and group T is not equal to 0
95 percent confidence interval:
-30.87724 23.98081
sample estimates:
mean in group C mean in group T
88.50528 91.95349 Derselbe Test, anders geschrieben:
t.test( plotsB$yield_C, plotsB$yield_T )
Welch Two Sample t-test
data: plotsB$yield_C and plotsB$yield_T
t = -0.26416, df = 17.96, p-value = 0.7947
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-30.87724 23.98081
sample estimates:
mean of x mean of y
88.50528 91.95349 Wenn wir aber die Daten “paaren”, d.h. jedem C-Wert den zugehörigen T-Wert zuweisen, und einen sog. “gepaarten t-Test” verwenden, dann gewinnen wir:
t.test( plotsB$yield_C, plotsB$yield_T, paired=TRUE )
Paired t-test
data: plotsB$yield_C and plotsB$yield_T
t = -4.0932, df = 9, p-value = 0.002704
alternative hypothesis: true mean difference is not equal to 0
95 percent confidence interval:
-5.353927 -1.542498
sample estimates:
mean difference
-3.448213 Was hier betrachtet haben, ist nicht mehr die Differenz der Mittelwerte, sondern der Mittelwert der Differenzen der Werte jedes Feldes.
Der gepaarte t-Test ist äquivalent zum “Ein-Stichproben-t-Test”, bei dem wir testen, ob der MIttelwert einer einzelnen Liste von Werten sich signifikant von 0 unterscheidet:
t.test( plotsB$yield_C - plotsB$yield_T )
One Sample t-test
data: plotsB$yield_C - plotsB$yield_T
t = -4.0932, df = 9, p-value = 0.002704
alternative hypothesis: true mean is not equal to 0
95 percent confidence interval:
-5.353927 -1.542498
sample estimates:
mean of x
-3.448213