dbinom( 3, 10, 1/6 )[1] 0.1550454Schätzung binomialer Anteile
Bernoulli-Experimente
Ein Zufallsexperiment mit zwei möglichen Ergebnissen heisst Bernoulli-Experiment. Man bezeichent die beiden möglichen Ergebnisse als “Erfolg” (success) und Fehlschlag (failure).
Beispiele:
- Münzwurf
- Wurf eines Würfels mit Frage “Ist es eine Sechs?”
- Einpflanzen eines Samens mit Frage “Keimt er oder nicht?”
- …
Binomial-Verteilung
Die Erfolgswahrscheinlichkeit eines Bernoulli-Experiments ist \(p\). Das Experiment wird \(n\) mal durchgeführt. Was ist die Wahrscheinlichkeit, dass es zu genau \(k\) Erfolgen (und \(n-k\) Fehlschlägen) kommt?
Die Verteilung von \(k\) heißt Binomialverteilung. In R berechnet man sie mit dbninom.
Beispiel: Wie wahrscheinlich ist es dass man genau \(k=3\) mal eine Sechs würfelt, wenn man \(n=10\) Würfel wirft und die Würfel nicht gezinkt sind, d.h. die Wahrscheinlichkeit einer Sech beträgt \(p=1/6\)?
Wie wahrschinlich ist es, 0, 1, 2, 3, … Sechsen zu erhalten?
library(tidyverse)
tibble( number_of_sixes = 0:10 ) %>%
mutate( probability = dbinom( number_of_sixes, 10, 1/6 ) )# A tibble: 11 × 2
number_of_sixes probability
<int> <dbl>
1 0 0.162
2 1 0.323
3 2 0.291
4 3 0.155
5 4 0.0543
6 5 0.0130
7 6 0.00217
8 7 0.000248
9 8 0.0000186
10 9 0.000000827
11 10 0.0000000165Hier eine graphische Darstellung:
tibble( number_of_sixes = 0:10 ) %>%
mutate( probability = dbinom( number_of_sixes, 10, 1/6 ) ) %>%
ggplot() + geom_col( aes( x=number_of_sixes, y=probability ) ) +
scale_x_continuous( breaks=0:10 )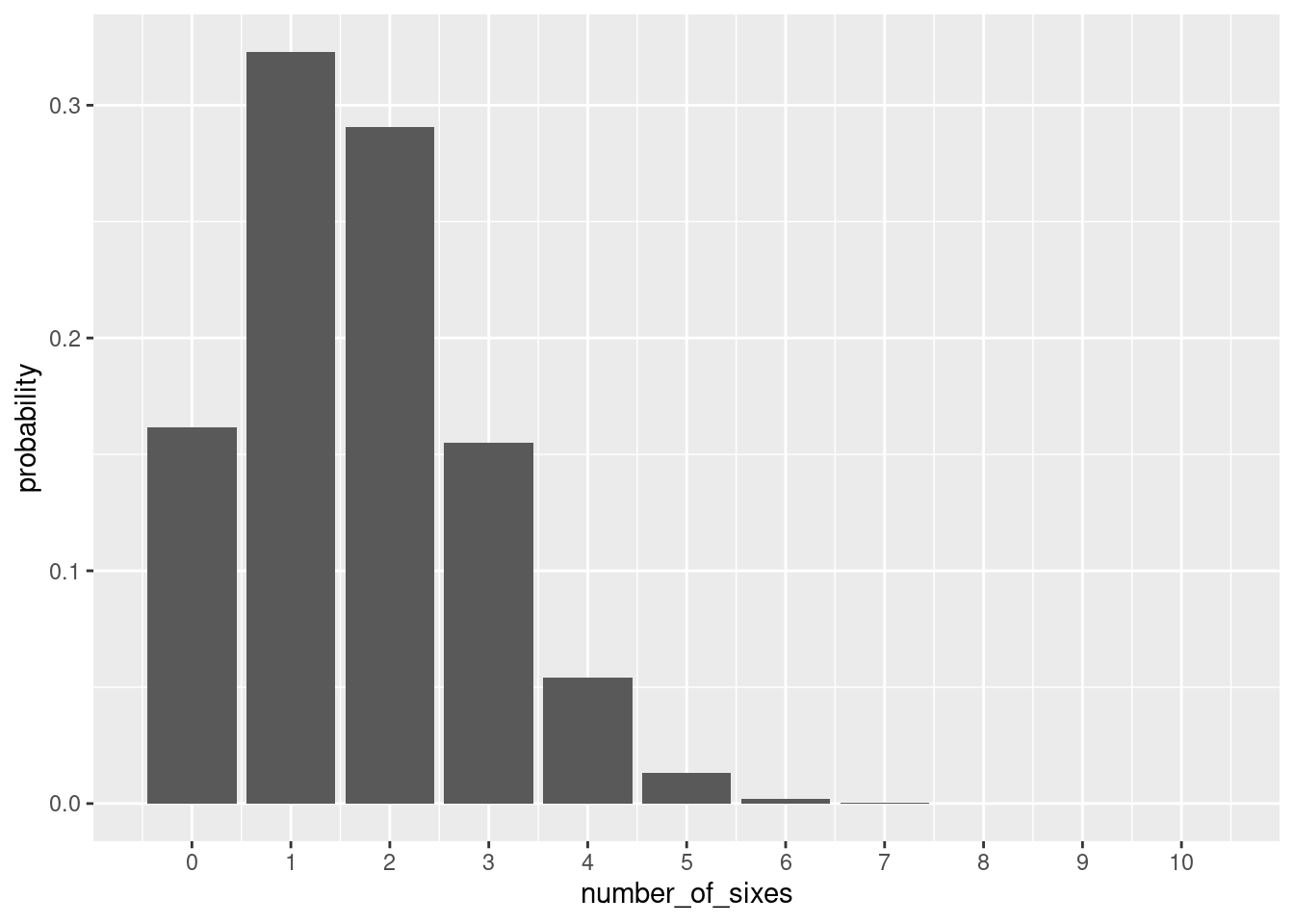
Formel für die Binomialverteilung
\[p_\text{binom}(k;n,p) = \binom{n}{k}p^k(1-p)^{n-k}\]
Momente
Die Binomialverteilung hat Erwartungswert \(\operatorname{E}(k)=np\) und Varianz \(\operatorname{Var}(k)=np(1-p)\).
Schätzen der Erfolgswahrscheinlichkeit
Wir möchten wissen, ob unser Würfel wirklich nicht gezinkt ist und werfen ihn \(n=600\) mal. Für \(p=1/6\) erwarten wir \(np=100\) Sechsen. Die tatsächlich beobachte Zahl \(k\) streut dann um den Erwartungsrt mit Standardabweichung \(\sqrt{np(1-p)}\approx 11.79\). Das sind 11% des erwarteten Wertes. Aus 600 Würfen können wir also die Wahrscheinlichkeit einer Sechs mit einem Standardfehler von 11% des Erwartungswerts schätzen.
Allgemeine Formel für den relativen Standardfehler der Schätzung eine Erfolgswahrscheinlichkeit: \[\operatorname{SD}(\hat p )=\frac{\operatorname{SD}(k)}{\operatorname{E}(k)} = \frac{\sqrt{np(1-p)}}{np} = \frac{1}{\sqrt{n}}\sqrt{\frac{1-p}{p}} \] Also: Wenn man die Genauigkeit der Schätzung einer Erfolgswahrscheinlichkeit verdoppeln möchte, braucht man viermal so viele Beobachtungen.
Dasselbe haben wir auch beim Mittelwert gelernt: Wenn man die Genauigkeit der Schätzung eines Mittelwerts verdoppeln möchte, braucht man ebenso viermal so viele Beobachtungen.
Konfidenzintervalle
Dasselbe Problem wie schon beim Mittelwert: Die Formel für den Standardfehler einer Wahrscheinlichkeit beinhaltet den wahren Wert von \(p\), den wir nicht kennen. Wenn wir statt dessen unseren Schätzwert \(\hat p = k/n\) einsetzen, bekommen wir leicht ein zu kleines Konfidenzintervall.
Beispiel: Wir haben unseren Würfel \(n=60\) mal geworfen und \(k=11\) mal eine Sechs erhalten. Wir suchen ein KI für die Wahrscheinlichkeit, eine Sechs zu erhalten.
Die Funktion binom.test liefert das gewünschte KI:
binom.test( 11, 60 )
Exact binomial test
data: 11 and 60
number of successes = 11, number of trials = 60, p-value = 7.561e-07
alternative hypothesis: true probability of success is not equal to 0.5
95 percent confidence interval:
0.09523582 0.30439605
sample estimates:
probability of success
0.1833333 Wieder ignorieren wir den p-Wert, da wir keinen test durchführen.
Die Mathematik hinter dem KI ist etwas kompliziert (siehe Wikipedia) und es gibt verschiedene Verfahren. Diwe Funktion binom.test verwendet das Verfahren von Clopper und Pearson (auch “exaktes KI” genannt).
Die folgende Funktion bietet eine Vielzahl von Verfahren
binom::binom.confint( 11, 60 ) method x n mean lower upper
1 agresti-coull 11 60 0.1833333 0.10383138 0.3009441
2 asymptotic 11 60 0.1833333 0.08542592 0.2812408
3 bayes 11 60 0.1885246 0.09569322 0.2871489
4 cloglog 11 60 0.1833333 0.09787069 0.2898770
5 exact 11 60 0.1833333 0.09523582 0.3043961
6 logit 11 60 0.1833333 0.10453210 0.3015352
7 probit 11 60 0.1833333 0.10175799 0.2967152
8 profile 11 60 0.1833333 0.09974812 0.2933943
9 lrt 11 60 0.1833333 0.09974401 0.2933915
10 prop.test 11 60 0.1833333 0.09932066 0.3085389
11 wilson 11 60 0.1833333 0.10557797 0.2991975Die Literatur empfiehlt das Verfahren von Wilson oder das von Agresti und Coull, aber eigentlich macht es kaum einen Unterschied.
Beispiel
Um die Sensitivität eines Corona-Schnelltest zu ermitteln, werden Nasenabstriche von 100 Patienten mit durch PCR bestätigter Covid19-Infektion auf Schnelltest-Kasetten gegeben. In 94 Fällen ist das Ergebnis positiv. Können wir mit 95% Konfidenz sagen, dass die Sensitivität des Tests mindestens 90% beträgt?
Binomial-Test
Beispiel 1: Ein Würfel wird \(n=600\) mal geworfen, dabei kommt es zu \(k=130\) Sechsen. Können wir die Nullhypothese ablehnen, dass die Wahrscheinlichkeit einer Sechs \(p=1/6\) beträgt, ist unser Ergebnis also statistische Evidenz, dass der Würfel gezinkt ist?
Wir berechnen, wie wahrscheinlich es ist, 130 oder mehr Sechsen zu erhalten:
sum( dbinom( 130:600, 600, 1/6 ) )[1] 0.0008721039Das nur aus Zufall so vielen Sechsen kommen, ist sehr unwahrscheinlich. Der Würfel ist also gezinkt.
Dieser statistische test heißt Binomial-Test. Er prüft, ob die Anzahl an Erfolgen in einem mehrfach wiederholten Bernoulli-Experiment statistisch signifikant von der Erwartung aufgrund einer a priori angenommen Wahrscheinlichkeit (hier: \(p=1/6\)) abweicht.
Die binom.test-Funktion führ den Test durch und ermittelt denselben p-Wert wie unsere Berechnung per Hand:
binom.test( 130, 600, 1/6, alternative="greater" )
Exact binomial test
data: 130 and 600
number of successes = 130, number of trials = 600, p-value = 0.0008721
alternative hypothesis: true probability of success is greater than 0.1666667
95 percent confidence interval:
0.1892486 1.0000000
sample estimates:
probability of success
0.2166667 Wenn wir vorab offen sind, ob die Abweichung von 1/6 nach oben oder nach unten geht, machen wir einen zweiseitigen Test:
binom.test( 130, 600, 1/6, alternative="two.sided" )
Exact binomial test
data: 130 and 600
number of successes = 130, number of trials = 600, p-value = 0.001457
alternative hypothesis: true probability of success is not equal to 0.1666667
95 percent confidence interval:
0.1843313 0.2518190
sample estimates:
probability of success
0.2166667 Beim zweiseitigen test wird die Wahrscheinlichkeit aller möglichen Anzahlen \(k\) an Sechsen aufaddiert, die weniger (oder gleich) wahrscheinlich sind wie die beobachtete Anzahl.
weitere Beispiele
Ein Biologe beobachtet Gänse und bestimmt deren Geschlecht. Er zählt 39 männliche und 55 weibliche Tiere. Ist das Beweis dafür, dass (zumindest in diesem Habitat) mehr Weibchen als Männchen leben?
Wir kreuzen zwei Pflanzen, die beide für ein Merkmal (z.B. Farbe der Erbsen) heterozygot sind. Nach Mendel würden wir für dominant-rezessiven Erbgang ein Verhältnis von 3:1 erwarten. Wir zählen in der nächsten Generation 270 Pflanzen mit dem dominanten Phänotyp (grüne Erbsen) 130 mit dem rezessiven Phänotyp (gelbe Erbsen). Ist die Abweichung stark genug, dass wir auf eine Abweichung von den Mendelschen Gesetzen schließen dürfen?
Ein Hersteller behauptet, dass höchstens 1% ihrer Produkte defekt ist. Wir kaufen 100 Einheiten, davon sind 4 defekt. Haben wir nur Pech gehabt, oder kannd er Hersteller sein Versprechen nicht halten?
Vergleich von Anteilen: Fisher-Test
Beispiel: Wir möchten wissen, ob die Bodentemperatur einen Einfluss auf das Keinen gewisser Samen hat. Wir pflanzen 400 Samen in kleine Töpfe. 200 Samen werden bei 20 °C gehalten und 200 Samen bei 23 °C. Die folgende Tabelle gibt an, wie viele Samen gekeimt sind (Spalte “yes”) und wie viele nicht (Spalte “no”). Die beiden Zeilen entsprechen den beiden Wachstumsbedingungen (“warmer” und “cooler”).
rbind(
warmer = c( yes=170, no=30 ),
cooler = c( 152, 48 ) ) -> ctbl
ctbl yes no
warmer 170 30
cooler 152 48Hier die Tabelle mit den Rand-Summen:
addmargins( ctbl ) yes no Sum
warmer 170 30 200
cooler 152 48 200
Sum 322 78 400Wir führen nun einen statistischen Test durch, ob die Keimungs-Wahrscheinlichkeit von der Temperatur beeinflusst wird.
Nullhypothese: Die Temperatur hat keinen Einfluss auf die Keimung.
Nullhypothese, weiter gedacht: 322 von 400 Samen sind gekeimt. Wie sich diese auf die warmen und kalten Plätze aufteilen, ist Zufall.
Simulation:
Die 400 Samen, gekeimt (1) oder nicht (0), zufällig permutiert:
sample( c( rep( 1, 322 ), rep( 0, 78 ) ) ) [1] 1 1 1 1 1 1 0 1 0 1 1 0 0 1 1 1 1 1 1 1 1 0 0 0 1 1 1 1 1 1 0 1 1 1 1 1 0
[38] 1 1 1 1 1 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 0 0 1 1 0 0 1
[75] 1 1 1 1 1 1 0 1 1 1 0 0 0 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1
[112] 1 1 1 0 0 1 1 1 1 0 1 1 0 1 1 1 0 0 0 1 1 0 0 1 1 0 1 1 1 1 1 1 1 1 1 1 1
[149] 1 1 1 1 1 1 1 0 1 1 1 1 1 0 1 1 1 1 1 0 1 0 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1
[186] 1 0 1 1 1 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 0 1 1 1 1 1 0 1 1 1 0 1 1
[223] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 1 1 0 1 1 0 1 0 1 1 0 0 1 1 1 0 1 1 1 1 0 1
[260] 1 1 1 1 1 1 1 1 1 0 0 1 1 1 1 1 1 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 1
[297] 1 1 1 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 0 1 1 1 1 1 1 0 1 1 1 1 0 0 1 0 0 1
[334] 1 1 1 0 1 1 1 0 1 1 1 1 1 0 1 1 1 1 1 0 0 1 1 1 1 1 0 1 0 1 1 0 1 1 1 1 0
[371] 1 0 1 1 1 1 1 1 0 1 1 1 1 0 0 0 1 1 0 1 1 1 1 1 1 0 1 0 1 1Die ersten 200 Position sind die warmen Plätze. Wie viele Keime sind dort?
sum( sample( c( rep( 1, 322 ), rep( 0, 78 ) ) )[ 1:200 ] )[1] 161Wir wiederholen das oft:
replicate( 10000, {
sum( sample( c( rep( 1, 322 ), rep( 0, 78 ) ) )[ 1:200 ] )
} ) -> null_germ_counts_in_coldHistgramm, mit beobachtetem Wert in rot:
hist( null_germ_counts_in_cold )
abline( v=170, col="red" )
Wie viele Werte in der Nullverteilung mindestens ebenso groß?
sum( null_germ_counts_in_cold >= 170 )[1] 162Unser Permutations-p-Wert ist also
( sum( null_germ_counts_in_cold >= 170 ) + 1 ) / ( length( null_germ_counts_in_cold ) + 1 )[1] 0.01629837Statt durch Permutationen zu simulieren, können wir die Wahrscheinlichkeit auch exakt berechnen, indem wir in ein Urnenmodell übersetzen: Eine Urne enthält 400 Kugeln, von denen 322 rot markiert sind. Wir ziehen 200 Kugeln (ohne Zurücklegen). Wie wahrscheinlich ist es, dass unter den gezogenen Kugeln mindestens 170 markierte Kugeln sind?
Die Antwort liefert die Formel für “Ziehen ohne Zurücklegen ohne Reihenfolge”, d.h., die hypergeometrische Verteilung:
phyper( 170-1, 322, 78, 200, lower.tail=FALSE )[1] 0.01574331Der Test, den wir eben durchgeführt haben, heißt Fisher-Test (oder: hypergeometrischer Test). Es gibt auch eine Funktion dazu:
fisher.test( ctbl, alternative="greater" )
Fisher's Exact Test for Count Data
data: ctbl
p-value = 0.01574
alternative hypothesis: true odds ratio is greater than 1
95 percent confidence interval:
1.136145 Inf
sample estimates:
odds ratio
1.786847 Es war a priori nicht klar, ob Wärme das Keimen fördert oder hemmt. Daher sollten wir besser einen zweiseitigen Test machen:
fisher.test( ctbl )
Fisher's Exact Test for Count Data
data: ctbl
p-value = 0.03149
alternative hypothesis: true odds ratio is not equal to 1
95 percent confidence interval:
1.049327 3.081167
sample estimates:
odds ratio
1.786847 Zusammenfassung
Wir haben ein Bernoulli-Experiment (“Keimt der Samen?”) mehrfach unter zwei Bedingungen (wärmer oder kälter) durchgeführt, und jeweils gezählt wie oft der Ausgang ein Erfolg (Keimung) war. Die Frage war, ob die Erfolgswahrscheinlichkeit von der Bedingung abhängt.
Dazu erstellen wir eine sog. Vier-Felder-Tafel (contingency table) mit zwei Zeilen für die beiden Bedingungen (wärmer, kälter) und zwei Spalten für die beiden Ergebnisse (keimt, keimt nicht). In die Felder schreiben wir, wie oft der jeweilige Falleingetreten ist.
Diese Tafel übergeben wir fisher.test. Dies testet die Nullhypothese, dass die Erfolgswahrscheinlichkeit sich zweischen den beiden Bedingungen nicht unterscheidet.
weitere Beispiele
- In einer klinischen Studie wird ein Medikament getestet. Die Patienten werden in zwei Gruppen eingeteilt, die entweder das Medikament erhalten oder ein Placebo. In jeder Gruppe wird gezählt, bei wie vielen Patienten eine Besserung eintritt.