library( tidyverse )
read_csv("data_on_git/nhanes.csv") %>%
filter( age >= 18, !is.na(height) ) -> nhanes_adultsANOVA
ANOVA = Analysis of Variance
One-way-ANOVA
Einführendes Beispiel
Unterscheidet sich in unseren NHANES-Daten die Körpergröße zwischen den Ethnien? Hat die Ethnie einen Einfluss auf die Körpergröße?
nhanes_adults %>%
group_by( ethnicity ) %>%
summarise( mean(height) )# A tibble: 6 × 2
ethnicity `mean(height)`
<chr> <dbl>
1 Mexican 163.
2 NH Asian 163.
3 NH Black 168.
4 NH White 168.
5 Other Hispanic 163.
6 Other/Mixed 170.Ist das statistisch singifikant?
Wir könnten t-Tests zwischen allen Paaren von Ethnien vornehmen, aber so genau brauchen wir es nicht. Wir möchten nur wissen, ob die Ethnie einen Einfluss hat, nicht, welche Ethnien größer und welche kleiner sind.
Vorbereitung: Wiederholung zur Varianz
Wir erinnern uns, wie die Varianz einer Liste von Werten, \(x_1,\dots,x_i,\dots,x_n\) berechnet wird:
Man bestimmt zunächst den Mittelwert \(\mu=\frac{1}{n}\sum_i x_i\).
Dann bestimmt man die Abweichung jedes Einzelwerte vom Mittelwert. Man erhält die sog. Residuen \(r_i=x_i-\mu\).
Man quadriert die Residuen und addiert die quadrierten Residuen: \(\text{SS} = \sum_i r_i^2 = \sum_i (x_i-\mu)^2\). Diesen Wert nennt man die Quadratsumme der Residuen (residual sum of squares, RSS, oder einfach nur sum of squares, SS)
Die Varianz ist der Mittelwert der quiadrierten Residuen.
Allerdings berechnet man den Mittelwert nicht, wie üblich, indem man die Quadratsumme durch \(n\) teilt, sondern man teilt durch \(n-1\) (Besselsche Korrektur), um die Verzerrung (bias) auszugleichen, die dadurch entsteht, dass der Mittelwert, den man abgezogen hat, nicht der Mittelwert der Grundgesamtheit, sondern der der Stichprobe ist, und daher die Quadratsumme etwas zu klein ist. Durch die Besselsche Korrektur wird die so geschätze Varianz erwartungstreu (unbiased), d.h., im Mittel über viele Stichproben ist sie gleich der wahren varianz der Grundgesamtheit.
Wenn wir in o.g. Verfahren den Mittelwert \(\mu\) durch irgendeinen anderen Wert ersetzt, wird die Quadratsumme größer, wie der folgende Satz aussagt:
Die Quadratsumme der Abweichungen einer Liste von Werten \(x_i\) von einem vorgegebenen Wert \(\mu\), also \(\sum_i(x_i-\mu)^2\) wird minimal, wenn \(\mu\) der Mittelwert der \(x_i\) ist.
Quadratsummen und Bestimmtheitsmaß
Wir berechnen die Quadratsumme für die Körpergrößen in der NHANES-Tabelle gegen den Mittelwert:
nhanes_adults %>%
mutate( mean_height = mean(height) ) %>%
mutate( residual = height - mean_height ) %>%
summarize( TSS = sum( residual^2 ) )# A tibble: 1 × 1
TSS
<dbl>
1 551604.Diesen Wert bezeichnet man als “total sum of squares” (TSS).
Nun wiederholen wir diese Rechnung, ziehen aber nicht den globalen Mittelwert ab, sondern den Mittelwert der jeweiligen Ethnie
nhanes_adults %>%
group_by( ethnicity ) %>%
mutate( mean_height = mean(height) ) %>%
mutate( residual = height - mean_height ) %>%
ungroup() %>%
summarize( RSS = sum( residual^2 ) ) # A tibble: 1 × 1
RSS
<dbl>
1 513932.Diese Quadratsumme heißt “residual sum of squares” (RSS).
Die Quadratsumme wurde um 6.8% reduziert, und es verbleiben 93.2%
513931.8 / 551603.5[1] 0.9317051Man sagt: Der Faktor “Ethnie” erklärt 6,8% der Varianz der Körpergröße. Der Wert 0.068 wird auch gerne als “Bestimmtheitsmaß” (coefficient of determination) oder \(R^2\) bezeichnet.
Allerdings ist das Verb “erklären” nicht ganz angemessen, denn auch ein zufälliger Faktor scheint Varianz zu erklären.
Um dies zu sehen, wiederholen wir die Berechnung von RSS, permutieren aber vorher die Ethnie-Labels:
nhanes_adults %>%
mutate( ethnicity = sample(ethnicity) ) %>% # <- Permutation
group_by( ethnicity ) %>%
mutate( mean_height = mean(height) ) %>%
mutate( residual = height - mean_height ) %>%
ungroup() %>%
summarize( RSS = sum( residual^2 ) ) # A tibble: 1 × 1
RSS
<dbl>
1 551371.Nun “erklären” wir etwa 0,14% der Varianz (wieder berechnet als (TSS-RSS)/TSS).
Damit wir wirklich sagen können, dass der Faktor “Ethnie” einen Einfluss auf die Körpergröße hat, sollte das Bestimmtheitsmaß also signifikant über diesem Wert liegen.
Die F-Statistik
Die F-Statstik ergibt sich nach folgender Formel:
\[ F = \frac{{(\text{TSS}-\text{RSS})/(k-1)}}{\text{RSS}/(n-1)} = R^2 \cdot \frac{n-1}{k-1}\] Hierbei ist \(n\) die Anzahl der Werte (bei uns $n=$5444) und \(k\) die Anzahl der Gruppen (bei uns \(k=6\) Ethnien).
Die F-Statistik ist so konstruiert, dass sie den Erwartungswert 1 hat, wenn die Gruppen-Zuordnung zufällig ist oder keinen Einfluss auf den Wert hat. Wie stark \(F\) um den Erwartungswert 1 schwankt, wenn die Nullhypothese (Gruppenzugehörigkeit hat keinen Einfluss) zutrifft, wird durch die \(F\)-Verteilung beschrieben, die durch \(k-1\) und \(n-1\) parametrisiert ist.
Bei uns ergibt sich \(F=79.7\). Das ist ein extrem hoher Wert. Das ein so hoher Wert unter der Nullhypothese auftaucht, ist extrem unwahrscheinlich, der p-Wert dafür, dass die Ethnie wirklich einen Einfluss auf die Körpergröße hat, ist also sehr klein.
Lineares Modell mit R
In R können wir all diese Berechnung mit der Funktion lm durchführen:
fit <- lm( height ~ ethnicity, nhanes_adults )
fit
Call:
lm(formula = height ~ ethnicity, data = nhanes_adults)
Coefficients:
(Intercept) ethnicityNH Asian ethnicityNH Black
163.4494 -0.7975 5.0309
ethnicityNH White ethnicityOther Hispanic ethnicityOther/Mixed
4.6555 -0.6223 6.1488 Hier hat R zunächst nur die Mittelwerte berechnet. Eine Ethnie (nämlich “Mexican”, weild as im Alphabet als erstes kommt) wurde als Referenz (base level) gewählt, und der Mittelwert hierzu steht bei “Intercept”. Die Abweichungen der anderen Mittelwerte von der Referenz kommen danach.
Wenn wir die Funktion summary auf das Ergebnis von lm anwenden, erhalten wir \(F\) und \(R^2\):
summary( fit )
Call:
lm(formula = height ~ ethnicity, data = nhanes_adults)
Residuals:
Min 1Q Median 3Q Max
-29.4803 -7.2049 -0.4803 6.9951 29.2197
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 163.4494 0.3576 457.059 <2e-16 ***
ethnicityNH Asian -0.7975 0.4984 -1.600 0.110
ethnicityNH Black 5.0309 0.4504 11.171 <2e-16 ***
ethnicityNH White 4.6555 0.4223 11.024 <2e-16 ***
ethnicityOther Hispanic -0.6223 0.5613 -1.109 0.268
ethnicityOther/Mixed 6.1488 0.6805 9.036 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 9.721 on 5438 degrees of freedom
Multiple R-squared: 0.06829, Adjusted R-squared: 0.06744
F-statistic: 79.72 on 5 and 5438 DF, p-value: < 2.2e-16Wir ignorieren die Tabelle zunächst, und sehen nur auf die letzten beiden Zeilen.
Wie sehen das Bestimmtheitsmaß, \(R^2\), den \(F\)-Wert und den zughörigen \(p\)-Wert, also die Wahrscheinlichkeit, mit der man einen mindestens so großen F-Wert unter Annahme der Nullhypothese erhalten würde.
Weiteres Beispiel
Wir konstruieren uns ein Beispiel.
Wir nehmen an, dass wir in unserem Wald 60 Wühlmäuse gefangen und gewogen haben und bemerkt haben, dass sich diese durch die Fellfarbe unterscheiden. Wir fragen uns, ob die Fellfarbe einen Einfluss auf das gewicht hat. Tatsächlich sind die gelblichen Mäuse im Mittel ein kleines bisschen schwerer.
set.seed( 1324 )
bind_rows(
tibble( mass = rnorm( 30, mean=12, sd=4 ), coat = "gray" ),
tibble( mass = rnorm( 20, mean=15, sd=4 ), coat = "yellowish" ),
tibble( mass = rnorm( 20, mean=12, sd=4 ), coat = "darkgray" ),
tibble( mass = rnorm( 15, mean=12, sd=4 ), coat = "brown" ) ) -> mouse_datasummary( lm( mass ~ coat, mouse_data ) )
Call:
lm(formula = mass ~ coat, data = mouse_data)
Residuals:
Min 1Q Median 3Q Max
-9.7205 -2.3576 0.0818 2.6977 8.0246
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 12.25640 1.00567 12.187 <2e-16 ***
coatdarkgray -0.29557 1.33038 -0.222 0.825
coatgray -0.02196 1.23169 -0.018 0.986
coatyellowish 2.13562 1.33038 1.605 0.112
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 3.895 on 81 degrees of freedom
Multiple R-squared: 0.05941, Adjusted R-squared: 0.02457
F-statistic: 1.705 on 3 and 81 DF, p-value: 0.1724Hier ist der F-Wert zu klein, und der p-Wert zu hoch, als dass wir sicher sagen könnten, dass Fellfarbe und Gewicht verbunden sind.
Adjustiertes Bestimmtheitsmaß
Wie wir oben gesehen haben, ist das Bestimmtheitsmaß auch bei Zutreffen der Nullhypothese nicht 0.
Durch eine Adjustierungs-Formel kann es so umgerechnet werden, dass es unter der Nullhypothese den Erwartungswert 0 hat. Dies ist das “adjusted R-squared” in der Formel oben.
One-way-ANOVA und t-Test
Wenn man nur zwei Gruppen hat, ist der p-Wert aus einer ANOVA derselbe wie der p-Wert aus einem Student-t-Test:
bind_rows(
tibble( value = rnorm( 20, mean=10, sd=2 ), group="A" ),
tibble( value = rnorm( 20, mean=12, sd=2 ), group="B" ) ) -> example_data
summary( lm( value ~ group, example_data ) )
Call:
lm(formula = value ~ group, data = example_data)
Residuals:
Min 1Q Median 3Q Max
-4.2184 -1.9401 -0.2372 1.9851 3.7413
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 9.7910 0.4688 20.886 < 2e-16 ***
groupB 2.1184 0.6630 3.195 0.00281 **
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 2.097 on 38 degrees of freedom
Multiple R-squared: 0.2118, Adjusted R-squared: 0.191
F-statistic: 10.21 on 1 and 38 DF, p-value: 0.002809t.test( value ~ group, example_data, var.equal=TRUE )
Two Sample t-test
data: value by group
t = -3.1953, df = 38, p-value = 0.002809
alternative hypothesis: true difference in means between group A and group B is not equal to 0
95 percent confidence interval:
-3.4605445 -0.7762881
sample estimates:
mean in group A mean in group B
9.791041 11.909458 Two-way ANOVA
Wir können auch den Einfluss mehrerer Kovariaten auf die Körpergröße untersuchen:
fit <- lm( height ~ ethnicity + gender, nhanes_adults )
fit
Call:
lm(formula = height ~ ethnicity + gender, data = nhanes_adults)
Coefficients:
(Intercept) ethnicityNH Asian ethnicityNH Black
156.74663 -0.48257 5.28806
ethnicityNH White ethnicityOther Hispanic ethnicityOther/Mixed
4.59331 -0.09729 5.37918
gendermale
13.68325 Das Referenz-Level ist nun die Merkmalskombination ethnicity=="Mexican" und gender=="female". Der erwartete Wert hierzu wird als “Intercept” bezeichnet. Den erwarteten Werte für alle anderen Merkmalskombination erhält man, indem man zum Intercept die Angegebenen Ethnie-Koeffizienten hinzu addiert (oder nichts addiert, falls die Ethnie “Mexican” ist) und den Gender-Koeffizienten für “male” hinzuzählt, falls man nicht bei “female” ist.
Für jeden Probanden \(i\) können wir nun anhand dessen Merkmale (Ethnie und Geschlecht) einen “gefitteten Wert” (fitted value) \(\hat y_i\) berechnen, der sich aus den Koeffizienten wie eben beschrieben ergibt. Probanden mit denselben merkmalen haben denselben fitted value.
Die RSS wird jetzt berechnet als die Sumem der quadrierten Abweichung der gefitteten Werte \(\hat y_i\) von den tatsächlichen Werten \(y_i\) der Körpergröße der Probanden: \(\text{RSS} = \sum_i (y_i - \hat y_i)^2\).
Die Koeffizienten wurden von lm so bestimmt, dass die sich aus ihnen ergebenden fitted values die RSS minimieren.
Dies nennt man die Methode der kleinsten Quadrate (least squares fit).
Wenn man nur einen Faktor hat, gibt es pro Gruppe einen Koeffizienten, und die gefitteten Werte sind die Mittelwerte der Gruppen
Hier haben wir 12 Gruppen (6 Ethnien und 2 Geschlechter), aber nur 7 Koeffizienten. Daher sind die gefitteten Werte nicht die Gruppen-Mittelwerte.
Die lm-Funktion muss also einen Ausgleich (fit) schaffen zwischen den beiden Faktoren.
F-Test
Wir können für jeden Faktor getrennt feststellen, ob er hinreichend Varianz erklärt. Dazu dient die Anova-Tabelle:
anova(fit)Analysis of Variance Table
Response: height
Df Sum Sq Mean Sq F value Pr(>F)
ethnicity 5 37672 7534 157.66 < 2.2e-16 ***
gender 1 254103 254103 5317.17 < 2.2e-16 ***
Residuals 5437 259829 48
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Weiteres Beispiel
Wir kommen zurück zu unseren Mäusen. Wir machen die gelblichen Mäuse etwas schwerer als zuvor und weisen jeder Maus ein Geschlecht zu:
set.seed( 1324 )
bind_rows(
tibble( mass = rnorm( 30, mean=12, sd=4 ), coat = "gray" ),
tibble( mass = rnorm( 20, mean=16, sd=4 ), coat = "yellowish" ),
tibble( mass = rnorm( 20, mean=12, sd=4 ), coat = "darkgray" ),
tibble( mass = rnorm( 15, mean=12, sd=4 ), coat = "brown" ) ) %>%
mutate( sex = sample( c("male","female"), n(), replace=TRUE ) ) -> mouse_data
fit <- lm( mass ~ coat + sex, mouse_data )
fit
Call:
lm(formula = mass ~ coat + sex, data = mouse_data)
Coefficients:
(Intercept) coatdarkgray coatgray coatyellowish sexmale
12.15901 -0.30252 -0.04979 3.17040 0.20869 Die Anova-Tabelle soltle ergeben, dass das geschlecht keinen Einfluss auf das Gewicht hat (da wir es ja zufällig zugewiesen haben):
anova(fit)Analysis of Variance Table
Response: mass
Df Sum Sq Mean Sq F value Pr(>F)
coat 3 161.32 53.774 3.5033 0.01912 *
sex 1 0.88 0.877 0.0571 0.81171
Residuals 80 1227.95 15.349
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Wir sehen uns auch die Koeffizienten noch mal an.
Für später wird es nützlich sein, schon jetzt folgendes zu veranschaulichen:
Für jede Maus bestimmen wir den “fitted value” als
\[ \hat y_i = \beta_0 + \beta_\text{darkgray}x_{i,\text{darkgray}}+ \beta_\text{gray}x_{i,\text{gray}}+ \beta_\text{yellowish}x_{i,\text{yellowish}} + \beta_\text{male}x_{i,\text{male}}\] Hier sind die \(beta\) die Koeffizienten udn die \(x_i\) sind “Indikator-Variablen”, die 1 sind, falls das entsprechende Merkmal bei Maus \(i\) vorliegt und sonst 0.
Die Methode der kleinsten Quadrate bedeutet, dass lm diejenigen Werte für die \(\beta\) gesucht hat, die \(\text{RSS}=(y_i-\hat y_i)^2\) so klein wie möglich macht.
Terminologie
Die Variablen, für die man Koeffizienten sucht (hier:
ethnicityundgenderbzw.sexundcoat) heißen unabhängige Variable (independent variables), Kovariaten (covariates), oder Prediktoren (predictors). Sie stehen imlm-Aufruf rechts der Tilde.Die Variable, deren Varianz man erklären will (hier:
heightbzw.mass) heisst abhängige Variable (dependent variable) oder Response.Die Werte für \(\beta\) heißen Koeffizienten (coefficients).
Die \(\hat y_i\) heißen “fitted values”, und die Abweichung der tatsächlichen Werte der abhängigen Variablen von ihren fitted values, also \(y_i-\hat y_i\), heissen Residuen (residuals).
Die Matrix, die durch die \(x\) gebilder wird, heißt Design-Matrix oder Modell-Matrix.
Interactions
Wir betrachten folgendes Modell:
lm( height ~ ethnicity + gender, nhanes_adults )
Call:
lm(formula = height ~ ethnicity + gender, data = nhanes_adults)
Coefficients:
(Intercept) ethnicityNH Asian ethnicityNH Black
156.74663 -0.48257 5.28806
ethnicityNH White ethnicityOther Hispanic ethnicityOther/Mixed
4.59331 -0.09729 5.37918
gendermale
13.68325 Der Fit hat ergeben, dass Mqnner im Schnitt 13,6 cm größer sind als Frauen. Gilt das für alle Ethnien? Oder gibt es Ethnien, wo der Unterschied zwischen Männern und Frauen größer oder kleiner ist als bei anderen Ethnien.
Hängt also der Unterschied zwischen den Geschlechtern von der Ethnie ab? In diesem Fall spricht man von einer Wechselwirkung (interaction) der beiden Faktoren.
Mit lm testet man das wie folgt:
Man fittet ein Modell mit Wechselwirkung, indem man einen Stern zwischen die möglicherweise wechselwirkenden Faktoren setzt:
fit <- lm( height ~ ethnicity * gender, nhanes_adults )
fit
Call:
lm(formula = height ~ ethnicity * gender, data = nhanes_adults)
Coefficients:
(Intercept) ethnicityNH Asian
156.73263 -0.56109
ethnicityNH Black ethnicityNH White
5.26542 4.49768
ethnicityOther Hispanic ethnicityOther/Mixed
0.64499 5.16269
gendermale ethnicityNH Asian:gendermale
13.71185 0.16963
ethnicityNH Black:gendermale ethnicityNH White:gendermale
0.04919 0.19316
ethnicityOther Hispanic:gendermale ethnicityOther/Mixed:gendermale
-1.64166 0.39349 Nun fragt man, ob das Hinzunehmen der zusäztlcihen Koeffizienten für dei Wechselwirkung den Fit signifikant verbessert hat
anova(fit)Analysis of Variance Table
Response: height
Df Sum Sq Mean Sq F value Pr(>F)
ethnicity 5 37672 7534 157.7383 <2e-16 ***
gender 1 254103 254103 5319.8667 <2e-16 ***
ethnicity:gender 5 371 74 1.5518 0.1702
Residuals 5432 259459 48
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Nein, die Wechselwirkung ist nicht signifikant.
Post-hoc-Test
Wir haben gesehen, dass die Körpergröße von der Ethnie abhängt. Aber welche Ethnien unterscheiden sich?
Dies findet man mit Tukey’s “Honest Significant Differences”-Test heraus:
fit <- lm( height ~ ethnicity + gender, nhanes_adults )
TukeyHSD( aov(fit) ) Tukey multiple comparisons of means
95% family-wise confidence level
Fit: aov(formula = fit)
$ethnicity
diff lwr upr p adj
NH Asian-Mexican -0.7974778 -1.8078683 0.2129126 0.2151871
NH Black-Mexican 5.0308627 4.1178964 5.9438290 0.0000000
NH White-Mexican 4.6554674 3.7993862 5.5115487 0.0000000
Other Hispanic-Mexican -0.6222624 -1.7600516 0.5155269 0.6257140
Other/Mixed-Mexican 6.1488359 4.7694505 7.5282213 0.0000000
NH Black-NH Asian 5.8283405 4.9320462 6.7246348 0.0000000
NH White-NH Asian 5.4529453 4.6146666 6.2912239 0.0000000
Other Hispanic-NH Asian 0.1752154 -0.9492400 1.2996709 0.9978268
Other/Mixed-NH Asian 6.9463137 5.5779059 8.3147215 0.0000000
NH White-NH Black -0.3753953 -1.0932599 0.3424694 0.6702807
Other Hispanic-NH Black -5.6531251 -6.6909202 -4.6153299 0.0000000
Other/Mixed-NH Black 1.1179732 -0.1801634 2.4161098 0.1379084
Other Hispanic-NH White -5.2777298 -6.2658525 -4.2896071 0.0000000
Other/Mixed-NH White 1.4933684 0.2345888 2.7521481 0.0094490
Other/Mixed-Other Hispanic 6.7710982 5.3061015 8.2360950 0.0000000
$gender
diff lwr upr p adj
male-female 13.66023 13.29267 14.02779 0In diesen Test ist eine Anpassung von p-Werten und Konfidenzintervallen an das multiple Testen bereits eingebaut.
Verzerrung durch fehlende Variable
(engl. “bias from omitted variable”)
Beispiel: Wir untersuchen eine gewisse Pflanzensorte in ihrem natürlichen Umfeld. Wir vermuten, dass die Bodenqualität, insbesondere der Salzgehalt, einen Einfluss auf das Wachstum hat. Wir suchen Pflanzen an vielen verschiedenen Orten, bestimmen den Salzgehalt des Bodens (der Einfachheit halber dichotomisiert: “niedrig” und “hoch”) und messen die Wuchshöhe der Pflanze. Außerdem bestimmen wir ob die Pflanze im direkten Sonnenlicht steht oder von anderen Pflanzen beschattet wird. Leider haben wir übersehen, dass unsere Pflanzen zu zwei Spezies derselben Familie gehören, die äußerlich schwer zu unterscheiden sind.
set.seed( 1321 )
tibble( species = sample( c("A", "B"), size = 350, replace = TRUE, prob = c(0.3, 0.7) ) ) %>%
mutate( salt = ifelse( species == "A",
sample( c( "high","low"), size = n(), replace = TRUE, prob = c(0.5,0.5) ),
sample( c( "high","low"), size = n(), replace = TRUE, prob = c(0.2,0.8) ) ) ) %>%
mutate( light = sample( c( "shade", "sun" ), size = n(), replace = TRUE, prob = c(0.5,0.5) ) ) %>%
mutate( height = ifelse( species=="A", 40, 70 ) + ifelse( light=="sun", 30, 0 ) + rnorm( n(), 0, 10 ) ) -> tbl
head(tbl)# A tibble: 6 × 4
species salt light height
<chr> <chr> <chr> <dbl>
1 B low shade 63.5
2 B low shade 73.2
3 A high shade 56.7
4 A high sun 95.5
5 B low sun 86.5
6 B low shade 61.9In unserer ersten ANOVA betrachten wir nur die Prediktoren salt und light:
fit <- lm( height ~ salt + light, tbl )
fit
Call:
lm(formula = height ~ salt + light, data = tbl)
Coefficients:
(Intercept) saltlow lightsun
52.39 11.08 30.57 Offensichtlich wächst die Pflanze höher, wenn die viel Licht und wenig Salz hat.
Beide Effekte scheinen signifikant zu sein:
anova(fit)Analysis of Variance Table
Response: height
Df Sum Sq Mean Sq F value Pr(>F)
salt 1 6398 6398 26.20 5.111e-07 ***
light 1 81247 81247 332.72 < 2.2e-16 ***
Residuals 347 84736 244
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Wenn wir aber die Spezies in die Liste der Prediktoren aufnehmen, hat der Salzgehalt keinen Effekt mehr:
fit <- lm( height ~ species + salt + light, tbl )
fit
Call:
lm(formula = height ~ species + salt + light, data = tbl)
Coefficients:
(Intercept) speciesB saltlow lightsun
39.961 27.782 1.191 31.750 anova(fit)Analysis of Variance Table
Response: height
Df Sum Sq Mean Sq F value Pr(>F)
species 1 51061 51061 521.6335 <2e-16 ***
salt 1 26 26 0.2619 0.6091
light 1 87425 87425 893.1243 <2e-16 ***
Residuals 346 33869 98
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Wie kann das sein?
Folgender Beeswarm-Plot erklärt den Effekt
library( ggbeeswarm )
ggplot( tbl, aes( x = str_c(light,"/",salt) ) ) +
geom_beeswarm(aes( y=height, col=species ), size=.7, cex=1.5 ) +
geom_errorbar( aes( ymin=conf.low,ymax=conf.high ), col="darkgray", width=.4,
data = ( tbl %>% group_by( salt, light ) %>% summarise( broom::tidy(t.test(height)) ) ) )`summarise()` has grouped output by 'salt'. You can override using the
`.groups` argument.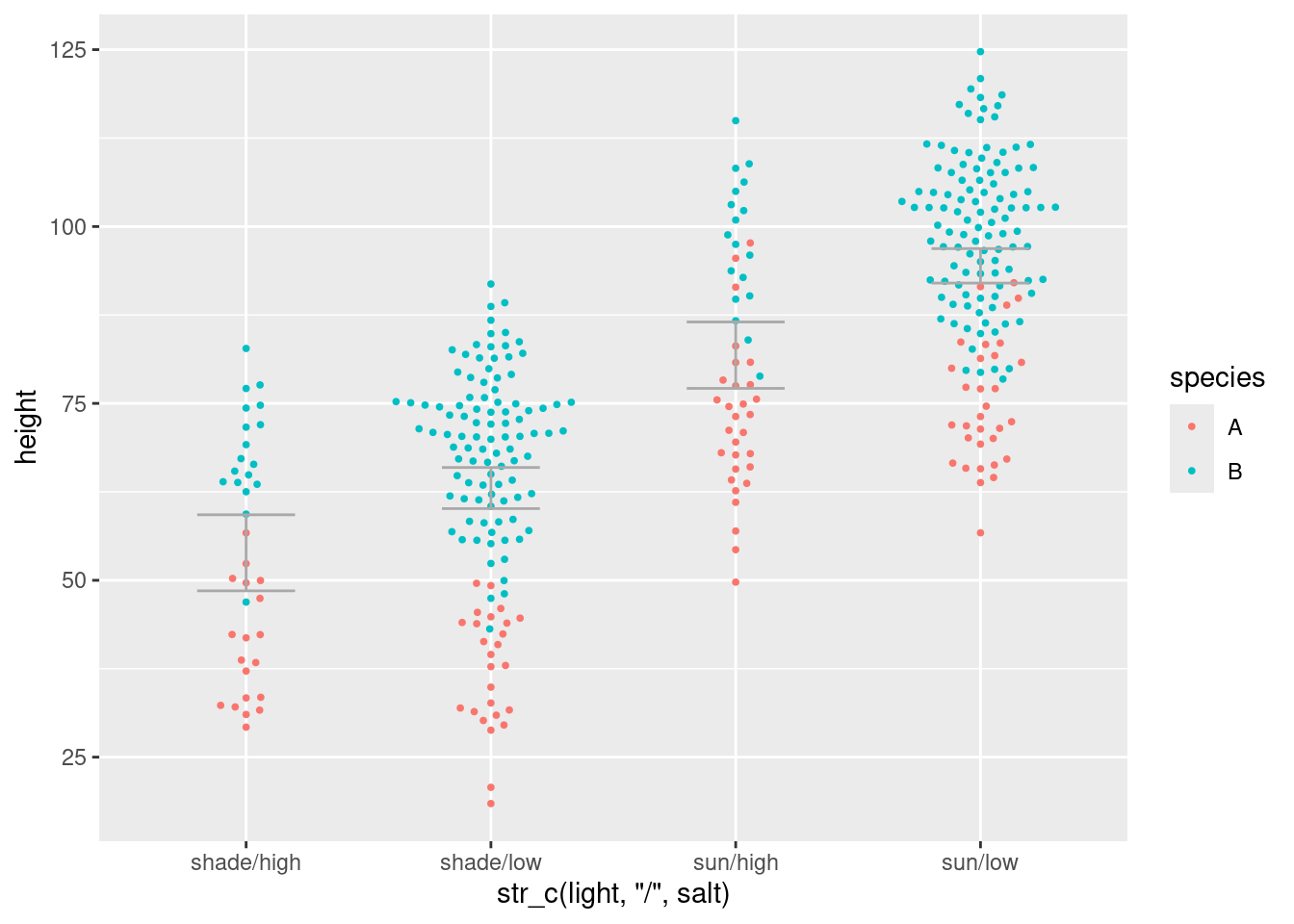
Zunächst scheint der Mittelwert der Größe bei Böden mit wenig Salz höher zu sein als bei salzigem Boden. Dann fällt uns aber auf, dass Spezies B wohl Probleme mit salzigem Böden hat, denn obwohl wir insgesamt Spezies B öfter gesammelt haben als Spezies A, zieht Spezies A bei den schlechten Böden gleich.
Wie zeichnen den Beeswarm
ggplot( tbl, aes( x = str_c(light,"/",salt) ) ) +
geom_beeswarm(aes( y=height, col=species ), size=.7, cex=1.5 ) +
geom_errorbar( aes( ymin=conf.low,ymax=conf.high ), col="darkgray", width=.4,
data = ( tbl %>% group_by( salt, light, species ) %>% summarise( broom::tidy(t.test(height)) ) ) ) +
facet_grid( ~ species )`summarise()` has grouped output by 'salt', 'light'. You can override using the
`.groups` argument.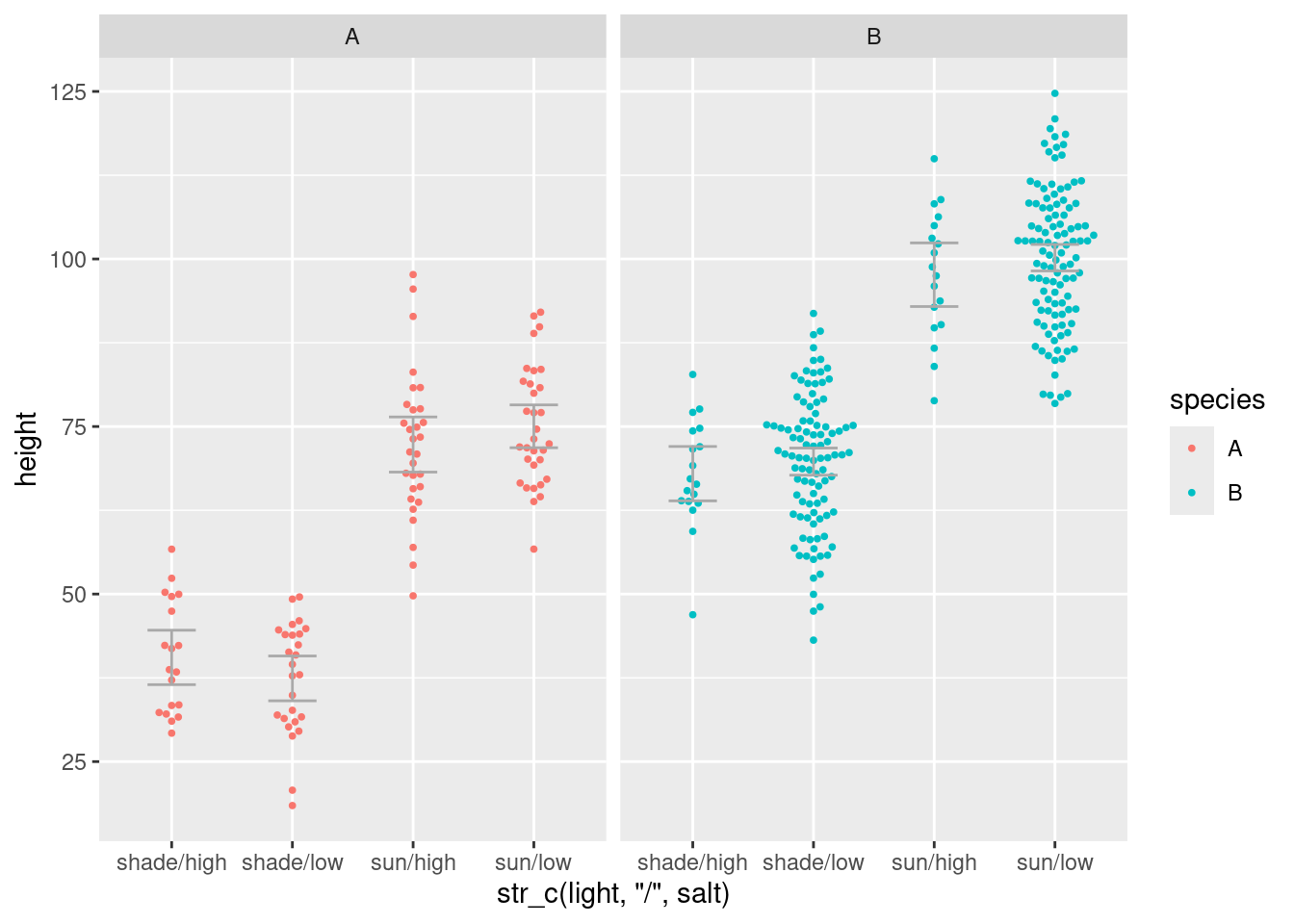
Also: Spezies A wächst allgemein weniger hoch als Spezies B. Da sie aber salzige Böden meidet, denkt man, dass das Salz die Wuchshöhe verringert, wenn man die beiden Spezies gemeinsam betrachtet. Wenn man aber die beiden Spezies getrennt betrachtet, verschwindet der Effekt.
Konfundierende und vermittelnde Faktoren
Das eben beobachtete Phänomen kann auf zwei Weisen entstehen:
Vermittlung
(mediation)
Ursache \(\rightarrow\) Mediator \(\rightarrow\) Response
Der Faktor “Ursache” beeinflusst die Response nicht direkt, sondern beeinflusst einen “vermittelnden” Faktor, der dann die Response beeinflusst.
Beispiel: Menschen, die wenig Sport machen, haben häufiger Diabetes Typ 2 als sportliche Menschen. Direkte Ursache des Diabetes ist aber Übergewicht, was aus der mangelnden körperlichen Betätigung resultiert.
zu wenig Bewegung \(\rightarrow\) Übergewicht \(\rightarrow\) Diabetes II
Konfundierung
(confounding)
Ein Faktor (“Confounder”) hat sowohl Einfluss auf den vermeintlichen Prediktor wie auch auf die Response.
Beispiel: Menschen, die viel rauchen, trinken oft auch viel Kaffee. Wenn wir das Auftreten von Atemwegskrankheiten auf Kaffeekonsum regressieren, könnten wir falsch folgern, dass Kaffee zu Atemwegserkrankungen führt.
Neigung zu Genussmittelsucht - \(\rightarrow\) Kaffeekonsum - \(\rightarrow\) Rauchen \(\rightarrow\) Atemwegserkrankungen
“Correlation does not imply Causation”