In dieser Übung benutzen wir die Daten aus dem Evo-Devo-Datensatz der Kaesmann-Gruppe für ein einfaches Beispiel zur Bestimmung differentiel exprimierter Gene (DGE).
Wir arbeiten wieder mit der Count-Matrix zur Maus und beschränken uns diesmal auf die Daten vom Herz, und zwar auf die zwei Zeitpunkte P3 und P63. Wir fragen, welche Gene sich zwischen jungen Mäusen (P3, also 3 Tage nach Geburt) und ausgewachsenen Mäusen (P63, also zwei Monate alt) in ihrer Expressionstärke im Herz ändern.
Laden Sie also zunächst die Count-Matrix und reduzieren Sie diese auf nur die 8 Proben vom Herz zu den Zeitpunkten P3 und P63. Sie können hierzu den Code aus der Vorlesung verwenden, mit dem wir dort die Matrix erst von breit auf lang pivotiert ahben, dann auf nur die Leber-Proben (diesmal eben, die benötigen Herz-Proben) reduziert haben.
So könnte die lange Tabelle aussehen:
Rows: 36141 Columns: 317
── Column specification ────────────────────────────────────────────────────────
Delimiter: "\t"
chr (1): gene_id
dbl (316): Brain_e10.5_1, Brain_e10.5_2, Brain_e10.5_3, Brain_e11.5_1, Brain...
ℹ Use `spec()` to retrieve the full column specification for this data.
ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message.
Joining with `by = join_by(sample)`
# A tibble: 289,128 × 6
gene_id sample columns tissue timepoint replicate
<chr> <chr> <dbl> <chr> <fct> <chr>
1 ENSMUSG00000000001 Heart_P3_1 2149 Heart P3 1
2 ENSMUSG00000000001 Heart_P3_2 2371 Heart P3 2
3 ENSMUSG00000000001 Heart_P3_3 2044 Heart P3 3
4 ENSMUSG00000000001 Heart_P3_4 2269 Heart P3 4
5 ENSMUSG00000000001 Heart_P63_1 1501 Heart P63 1
6 ENSMUSG00000000001 Heart_P63_2 1012 Heart P63 2
7 ENSMUSG00000000001 Heart_P63_3 756 Heart P63 3
8 ENSMUSG00000000001 Heart_P63_4 1137 Heart P63 4
9 ENSMUSG00000000003 Heart_P3_1 0 Heart P3 1
10 ENSMUSG00000000003 Heart_P3_2 0 Heart P3 2
# ℹ 289,118 more rows
Falls Ihr Computer mit der sehr großen Ausgangs-Matrix nicht zurecht kommt, können Sie auch diese Matrix laden, die nur die benötigten 8 Proben enthält:
# A tibble: 36,141 × 9
gene_id Heart_P3_1 Heart_P3_2 Heart_P3_3 Heart_P3_4 Heart_P63_1 Heart_P63_2
<chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 ENSMUSG0… 2149 2371 2044 2269 1501 1012
2 ENSMUSG0… 0 0 0 0 0 0
3 ENSMUSG0… 478 570 511 532 97 46
4 ENSMUSG0… 271 241 294 256 74 32
5 ENSMUSG0… 1 0 1 2 4 0
6 ENSMUSG0… 2170 2765 2413 3075 5838 2976
7 ENSMUSG0… 2070 2710 2393 1945 3101 2429
8 ENSMUSG0… 2454 3089 2405 2245 4539 2289
9 ENSMUSG0… 1809 2199 1825 2373 1762 929
10 ENSMUSG0… 11090 14032 13048 10557 18465 13336
# ℹ 36,131 more rows
# ℹ 2 more variables: Heart_P63_3 <dbl>, Heart_P63_4 <dbl>
Normalisieren Sie nun die Count-Werte, indem Sie auf CPM (counts per million) umrechnen. Berechnen Sie dann die logarithmische Expressionsstärke, wieder als lcpm = log10( cpm + 0.03). Sie sollten eine Tabelle in etwa wie diese erhalten:
# A tibble: 289,128 × 5
# Groups: sample [8]
gene_id sample count cpm lcpm
<chr> <chr> <dbl> <dbl> <dbl>
1 ENSMUSG00000000001 Heart_P3_1 2149 104. 2.02
2 ENSMUSG00000000001 Heart_P3_2 2371 98.0 1.99
3 ENSMUSG00000000001 Heart_P3_3 2044 98.9 2.00
4 ENSMUSG00000000001 Heart_P3_4 2269 87.2 1.94
5 ENSMUSG00000000001 Heart_P63_1 1501 51.0 1.71
6 ENSMUSG00000000001 Heart_P63_2 1012 62.1 1.79
7 ENSMUSG00000000001 Heart_P63_3 756 36.2 1.56
8 ENSMUSG00000000001 Heart_P63_4 1137 39.2 1.59
9 ENSMUSG00000000003 Heart_P3_1 0 0 -1.52
10 ENSMUSG00000000003 Heart_P3_2 0 0 -1.52
# ℹ 289,118 more rows
Nun können Sie über die Replikate mitteln, um einmal die Mittwelwerte für P3 und einmal für P36 zu erhalten. Setzen Sie die Werte nebeneinander, z.B. so:
Joining with `by = join_by(sample)`
`summarise()` has grouped output by 'gene_id'. You can override using the
`.groups` argument.
# A tibble: 36,141 × 3
# Groups: gene_id [36,141]
gene_id P3 P63
<chr> <dbl> <dbl>
1 ENSMUSG00000000001 1.99 1.66
2 ENSMUSG00000000003 -1.52 -1.52
3 ENSMUSG00000000028 1.36 0.511
4 ENSMUSG00000000037 1.07 0.225
5 ENSMUSG00000000049 -1.18 -0.731
6 ENSMUSG00000000056 2.05 2.25
7 ENSMUSG00000000058 2.00 2.01
8 ENSMUSG00000000078 2.05 2.12
9 ENSMUSG00000000085 1.95 1.77
10 ENSMUSG00000000088 2.73 2.89
# ℹ 36,131 more rows
Bestimmen Sie nun die Gene, für die das Expressions-Verhältnis P63 zu P3 am größten ist. Denken Sie daran, dass Sie auf einer logarithmischen Skala arbeiten: Unser Expressionsverhältnis wird also zu einer Differenz. Hier ist mein Ergebnis:
# A tibble: 36,141 × 4
# Groups: gene_id [36,141]
gene_id P3 P63 diff_log10_P63_P3
<chr> <dbl> <dbl> <dbl>
1 ENSMUSG00000026418 3.11 -0.189 -3.30
2 ENSMUSG00000040856 1.69 -0.840 -2.53
3 ENSMUSG00000029814 1.69 -0.742 -2.43
4 ENSMUSG00000063446 0.973 -1.35 -2.32
5 ENSMUSG00000054446 0.843 -1.32 -2.16
6 ENSMUSG00000013415 1.28 -0.787 -2.07
7 ENSMUSG00000096445 0.620 -1.44 -2.06
8 ENSMUSG00000062393 1.09 -0.947 -2.04
9 ENSMUSG00000027966 1.42 -0.615 -2.03
10 ENSMUSG00000051159 1.56 -0.444 -2.00
# ℹ 36,131 more rows
Üblicherweise verwendet man für logarithmische Expressionsverhältnisse (“log fold change”, LFC) den Logarithmus zur Basis 2, nicht zur Basis 10. Rechnen Sie um. Fügen Sie auch die Gen-Namen an.
Hier ist das Ergebnis meines Codes:
Rows: 56305 Columns: 3
── Column specification ────────────────────────────────────────────────────────
Delimiter: "\t"
chr (3): Gene stable ID, Gene name, Gene description
ℹ Use `spec()` to retrieve the full column specification for this data.
ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message.
Joining with `by = join_by(gene_id)`
# A tibble: 15 × 6
# Groups: gene_id [15]
gene_id P3 P63 l2fc_P63_P3 gene_name gene_descr
<chr> <dbl> <dbl> <dbl> <chr> <chr>
1 ENSMUSG00000026418 3.11 -0.189 -11.0 Tnni1 troponin I, skeletal, …
2 ENSMUSG00000040856 1.69 -0.840 -8.41 Dlk1 delta like non-canonic…
3 ENSMUSG00000029814 1.69 -0.742 -8.06 Igf2bp3 insulin-like growth fa…
4 ENSMUSG00000063446 0.973 -1.35 -7.70 Plppr1 phospholipid phosphata…
5 ENSMUSG00000054446 0.843 -1.32 -7.18 Cpa1 carboxypeptidase A1, p…
6 ENSMUSG00000013415 1.28 -0.787 -6.87 Igf2bp1 insulin-like growth fa…
7 ENSMUSG00000096445 0.620 -1.44 -6.84 Dcpp1 demilune cell and paro…
8 ENSMUSG00000062393 1.09 -0.947 -6.76 Dgkk diacylglycerol kinase …
9 ENSMUSG00000027966 1.42 -0.615 -6.74 Col11a1 collagen, type XI, alp…
10 ENSMUSG00000051159 1.56 -0.444 -6.66 Cited1 Cbp/p300-interacting t…
11 ENSMUSG00000056758 0.759 -1.24 -6.65 Hmga2 high mobility group AT…
12 ENSMUSG00000041431 1.62 -0.369 -6.62 Ccnb1 cyclin B1 [Source:MGI …
13 ENSMUSG00000033491 1.43 -0.549 -6.57 Prss35 protease, serine 35 [S…
14 ENSMUSG00000028175 0.995 -0.982 -6.57 Depdc1a DEP domain containing …
15 ENSMUSG00000096278 0.694 -1.24 -6.43 Dcpp2 demilune cell and paro…
Erinnern Sie sich, wie wir die Tabelle mit der Zuordnung von Ensembl-Gen-IDs zu Gen-Symbolen aus dem Ensembl BioMart herunter geladen haben? Versuchen Sie das selbst.
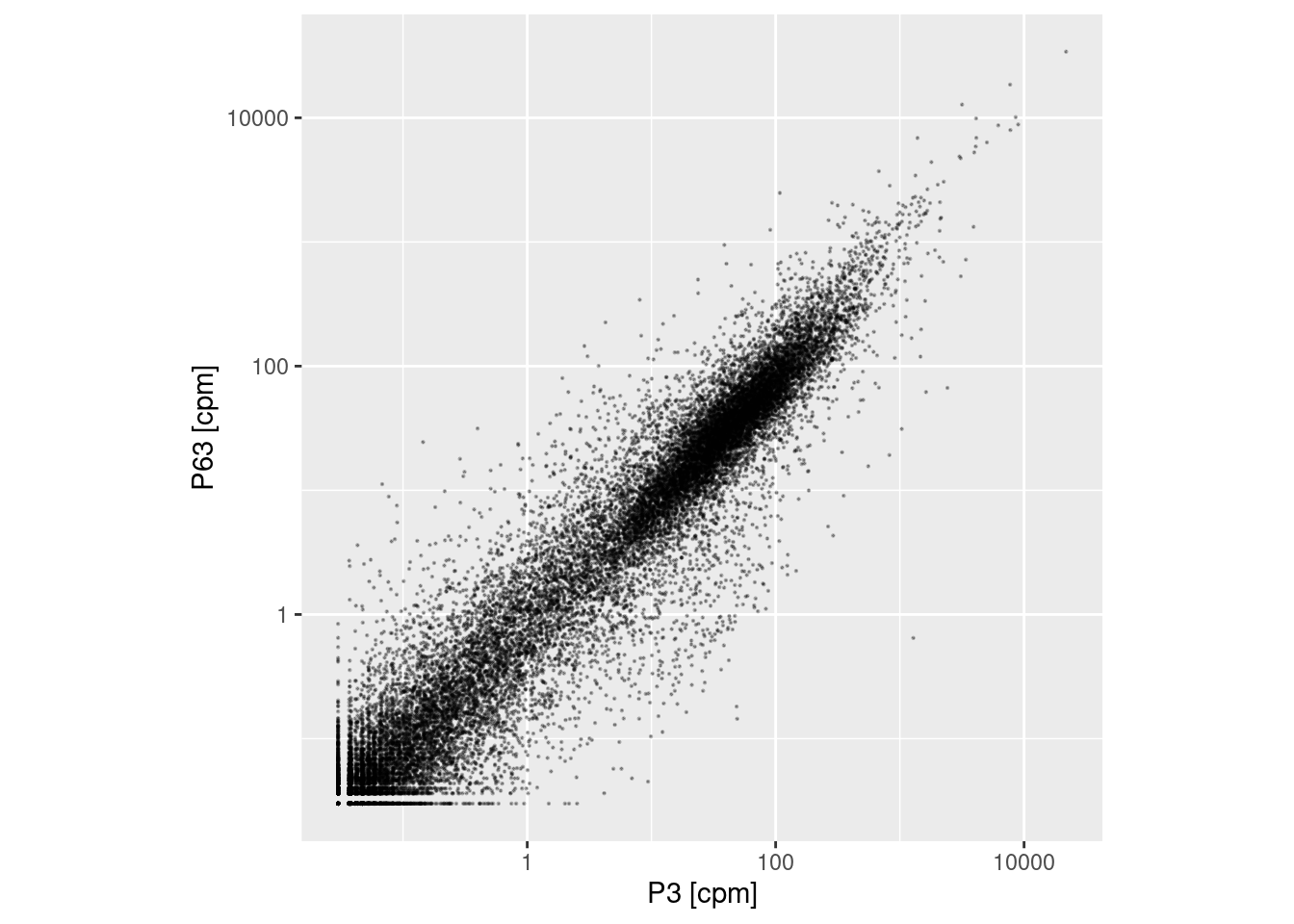
Zurück zu den DGEs. Plotten Sie die mittlere Expression zu P63 gegen die zu P3. Ihr Plot könnte z.B. so aussehen
(Mein Plot ist alledings nicht perfekt: Der Punkt ganz links unten entspricht 0 CPM in allen Replikaten; die Achsen sind dort aber nicht korrekt mit 0 beschriftet.)
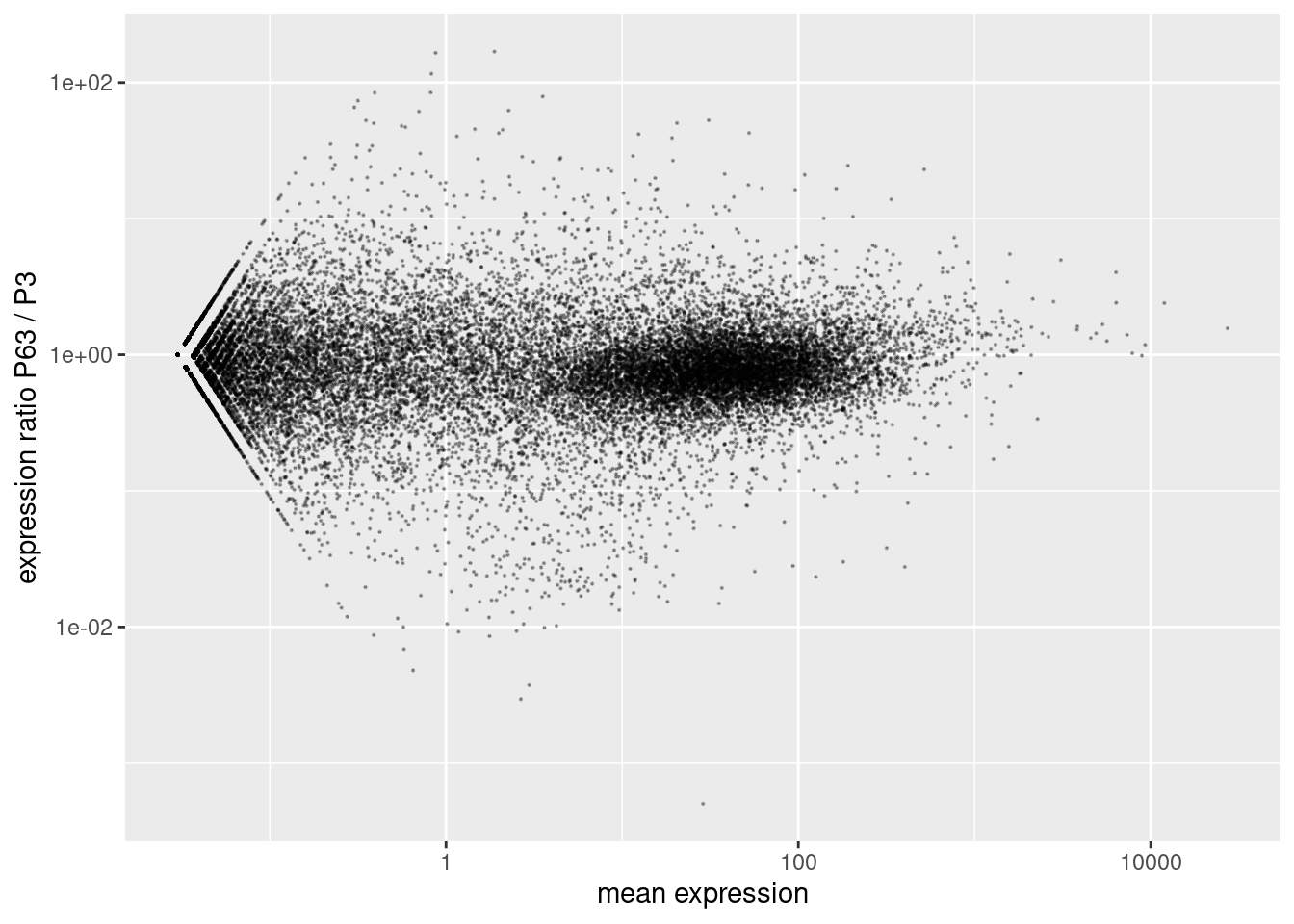
Gerne verwendet man hier einen sog. MA-Plot. Dazu verwendet man den Mittelwert über beide Gruppen als x-Achse und das logarithmische Verhältnis als y-Achse:
Erstellen Sie diesen Plot. Können Sie sehen, dass das derselbe Plot wie zuvor ist, nur um 45 Grad gedreht, und mit “gedehnter” y-Achse?
Warum scheint man bei niedrig exprimierten Genen deutlich stärkere Unterschiede zu sehen?
Gehen wir nun zurück zu den Genen, die in P63 deutlich stärker als in P3 exprimiert sind. Erstellen Sie eine Liste mit den 50 Genen mit den größtem Expressions-Verhältnissen.
[1] "ENSMUSG00000026418" "ENSMUSG00000040856" "ENSMUSG00000029814"
[4] "ENSMUSG00000063446" "ENSMUSG00000054446" "ENSMUSG00000013415"
[7] "ENSMUSG00000096445" "ENSMUSG00000062393" "ENSMUSG00000027966"
[10] "ENSMUSG00000051159" "ENSMUSG00000056758" "ENSMUSG00000041431"
[13] "ENSMUSG00000033491" "ENSMUSG00000028175" "ENSMUSG00000096278"
[16] "ENSMUSG00000051048" "ENSMUSG00000073948" "ENSMUSG00000063632"
[19] "ENSMUSG00000037568" "ENSMUSG00000052353" "ENSMUSG00000022033"
[22] "ENSMUSG00000056972" "ENSMUSG00000026683" "ENSMUSG00000020330"
[25] "ENSMUSG00000024598" "ENSMUSG00000037335" "ENSMUSG00000036223"
[28] "ENSMUSG00000027715" "ENSMUSG00000044201" "ENSMUSG00000041064"
[31] "ENSMUSG00000027654" "ENSMUSG00000052854" "ENSMUSG00000048327"
[34] "ENSMUSG00000027379" "ENSMUSG00000028678" "ENSMUSG00000068122"
[37] "ENSMUSG00000047844" "ENSMUSG00000028068" "ENSMUSG00000019942"
[40] "ENSMUSG00000040204" "ENSMUSG00000054196" "ENSMUSG00000026955"
[43] "ENSMUSG00000027326" "ENSMUSG00000051378" "ENSMUSG00000032218"
[46] "ENSMUSG00000028873" "ENSMUSG00000028197" "ENSMUSG00000026622"
[49] "ENSMUSG00000020914" "ENSMUSG00000046591"
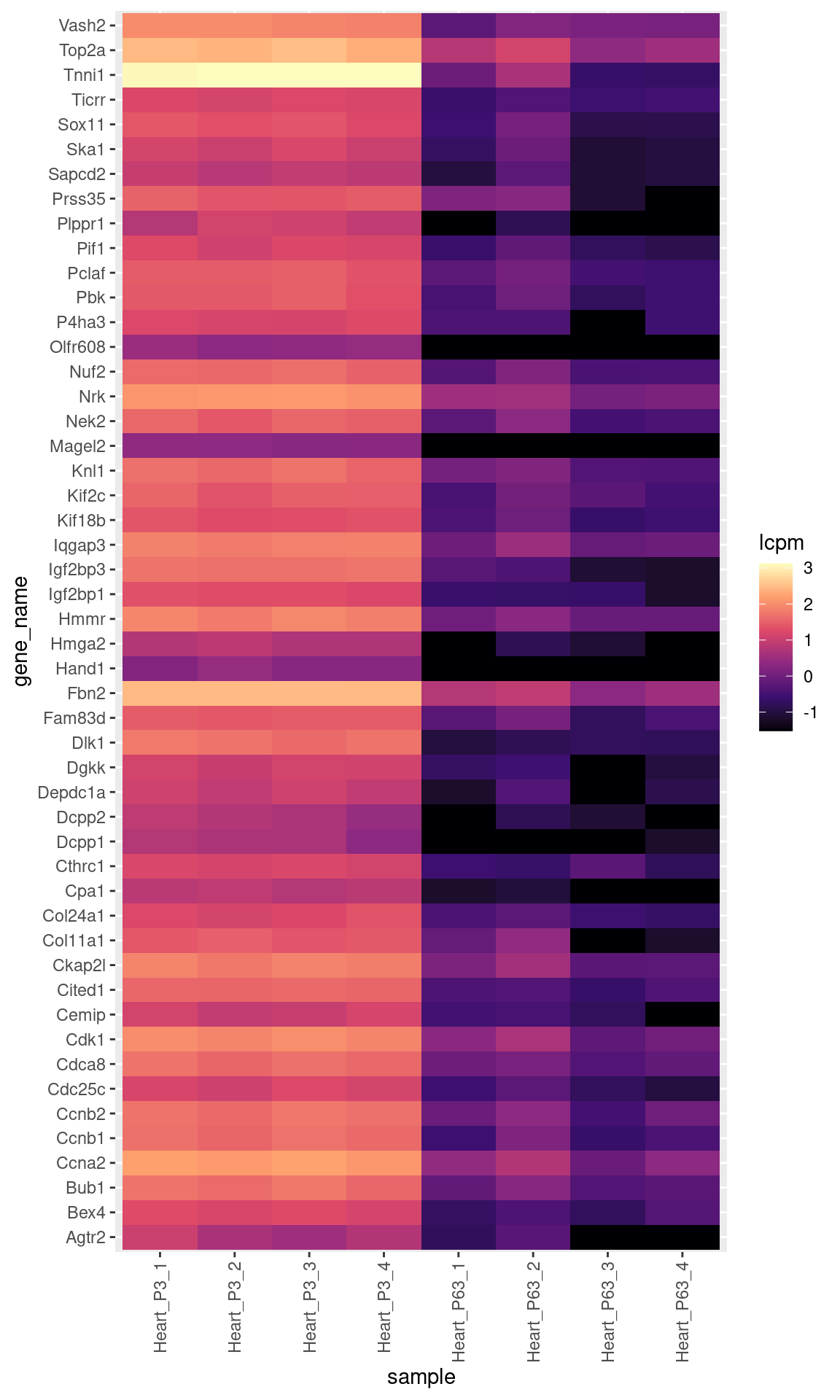
Stellen Sie nun die Werte der einzelnen Replikate für diese Gene als Heatmap dar
Joining with `by = join_by(gene_id)`
Entnehmen Sie nun für eines dieser Gene die log-CPM-Einzelwerte und führen Sie einen t-Test durch.
HIer z.B. für Cemip:
Joining with `by = join_by(gene_id)`
Joining with `by = join_by(sample)`
Welch Two Sample t-test
data: lcpm by timepoint
t = 7.5192, df = 3.3248, p-value = 0.003385
alternative hypothesis: true difference in means between group P3 and group P63 is not equal to 0
95 percent confidence interval:
1.123702 2.626872
sample estimates:
mean in group P3 mean in group P63
1.0561205 -0.8191667
Ausblick
Hier haben wir die stark differentiell exprimierten Gene per Hand gefunden. Dieses Vorgehen ist mühsam, aber leicht nachvollziehbar.
Allerdings hat es einige Probleme:
Bei sehr schwach exprimierten Genen können schon ein oder zwei zusätzliche Reads das Expressionsverhältnis stark ändern und soclhe keine Fluktuationen den Anschein starker Expressions-Änderungen erwecken.
Die Addition von 0.03 zur Behandlung von 0 Reads ist ad hoc und mathematisch schlecht motiviert.
Bis auf den t-Test am Schluss haben wir keinerlei Versuche gemacht, sicher zu stellen, dass alle 4 Replikate ein konsistentes Bild geben.
Wenn in einer Probe ein Gen außergewöhnlich hoch exprimiert ist, erscheinen alle anderen Gene etwas schwächer exprimiert, da wir auf Anteile schauen. Auch wenn die Gene tatsächlich weniger Anteil an allen Reads haben, wenn ein einzelnes Gen eine großen Teil der Reads für sich beansprucht, wäre es dennoch nicht hilfreich, alle Gene als herunter-reguliert zu betrachten.
Aus diesen Gründen gibt es eine Reihe von statistischen Methoden, die eine etwas ausgeklügeltere Analyse anbieten, und die man daher in der Praxis der einfachen Methode, die wir hier verwendet haben, vorzieht. Wir werden diese in einer der nächsten Vorlesungen ausprobieren.