suppressPackageStartupMessages( library(tidyverse) )
set.seed( 13245768 )Konfidenzintervalle für Differenzen und t-Tests
Vorlesung “Datenanalyse in der Biologie”
“Zwiebel”-Hausaufgabe
In der Hausaufgabe sollte simuliert werden, wie 10 Zwiebeln geerntet werden, von einem Feld, in dem Zwiebel-Massen normalverteilt sind mit Erwartungswert 80 g und Standardabweichung 9 g:
onions_control <- rnorm( 10, mean=80, sd=9 )Eine weitere Stichprobe aus 10 Zwiebeln wurde geerntet von einem Feld, wo der Erwartungswert der Masse um 8 g höher liegt, da das Feld mit einem Dünger behandelt wurde..
onions_treated <- rnorm( 10, mean=88, sd=9 )Wir berechnen Mittelwerte und Standardfehler dieser beiden Stichproben. Zunächst per Hand, und für die Zwiebeln vom ungedüngten “control field”:
mean_control <- mean( onions_control )
sem_control <- sd( onions_control ) / sqrt( length(onions_control) )
# length(onions_control) = 10 (Anzahl der Zwiebeln)
sf <- qt( 0.975, length(onions_control) - 1 ) # sf: "Student factor"
ci_control <- c( mean_control - sf*sem_control, mean_control + sf*sem_control )
ci_control[1] 72.38311 84.29864Hier dasselbe nochmal mit Verwendung der t.test-Funktion:
tres <- t.test( onions_control )
tres$conf.int[1] 72.38311 84.29864
attr(,"conf.level")
[1] 0.95Zur Erinnerung: t.test gibt uns auch den Mittelwert, im Slot “estimate”:
tres$estimatemean of x
78.34088 Für die gedüngten Zwiebeln (“treated field”) erhalten wir:
tres <- t.test( onions_treated )
tres$conf.int[1] 80.86784 97.88361
attr(,"conf.level")
[1] 0.95Die beiden Konfidenz-Intervalle überlappen sich. Wenn wir nicht wüssten, dass die wahren Erwartungswerte 80 g und 88 g sind (und als Experimentatoren würden wir das nicht wissen), dann würden wir aus diesen Beobachtungen nicht die Schlussfolgerung ziehen wollen, dass der Dünger die Zwiebel-Masse wirklich erhöht. Es erschiene uns sehr gut möglich, dass der Erwartungswert bei beiden Feldern derselbe ist.
Übrigens: Manchmal stört es, dass t.test immer so einen großen Block ausgibt. Die Funktion broom::tidy formt die Ausgabe zu einer Tabelle mit einer Zeile um. Das ist nützlich, wenn man t.test in einer Tidyverse-Pipeline benutzt, wie wir gleich sehen werden:
t.test( onions_control ) %>% broom::tidy()# A tibble: 1 × 8
estimate statistic p.value parameter conf.low conf.high method alternative
<dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <chr> <chr>
1 78.3 29.7 2.68e-10 9 72.4 84.3 One Samp… two.sided Graphische Darstellung
Nun möchten wir unsere Daten in einem Plot darstellen.
Dazu erstellen wir zunächst eine Tabelle:
bind_rows(
tibble( weight = onions_control, field = "control" ),
tibble( weight = onions_treated, field = "treated" ) ) -> onion_tbl
onion_tbl# A tibble: 20 × 2
weight field
<dbl> <chr>
1 75.0 control
2 69.7 control
3 73.2 control
4 85.8 control
5 65.5 control
6 90.2 control
7 86.6 control
8 71.9 control
9 83.1 control
10 82.5 control
11 95.8 treated
12 78.3 treated
13 110. treated
14 82.8 treated
15 77.7 treated
16 95.4 treated
17 107. treated
18 87.1 treated
19 79.8 treated
20 80.4 treatedDann bestimmen wir nochmals die Mittelwerte und ihre KIs:
onion_tbl %>%
group_by( field ) %>%
summarise( broom::tidy( t.test( weight ) ) ) %>%
select( field, mean=estimate, conf.low, conf.high ) -> mean_and_ci
mean_and_ci# A tibble: 2 × 4
field mean conf.low conf.high
<chr> <dbl> <dbl> <dbl>
1 control 78.3 72.4 84.3
2 treated 89.4 80.9 97.9Nun können wir plotten:
ggplot( NULL ) +
geom_point( aes( x=field, y=weight ), data = onion_tbl,
position = position_jitter( width=.1, height = 0 ) ) +
geom_errorbar( aes( x=field, ymin=conf.low, ymax=conf.high ), data = mean_and_ci,
width = .3 ) +
geom_errorbar( aes( x=field, ymin=mean, ymax=mean ), data = mean_and_ci,
width = .15 ) 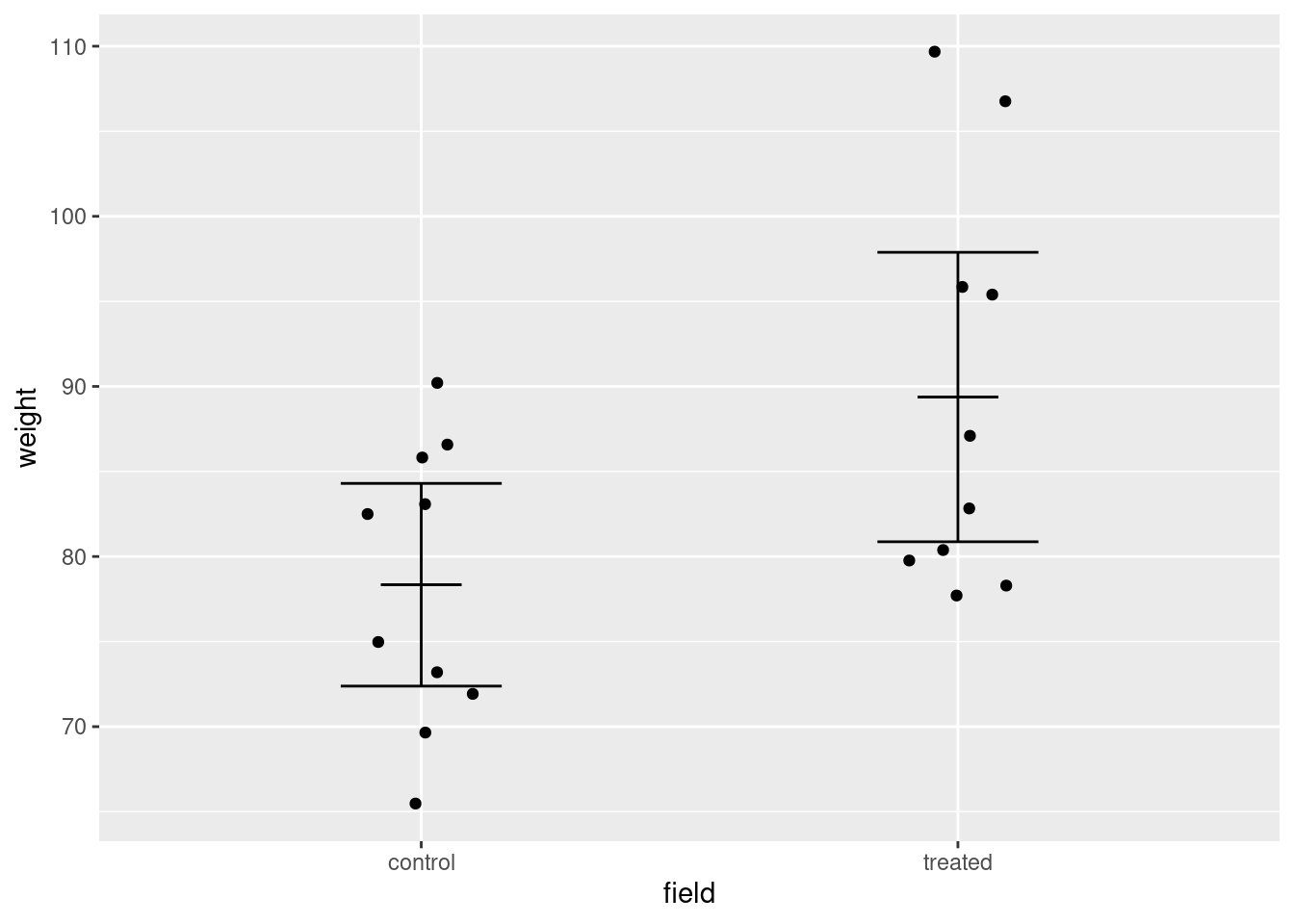
Neu hier:
ggplotbekommt keine Daten (NULL). Stattdessen bekommt jedesgeomseine eigenen Daten viadata.geom_errorbarzeichnet Fehlerbalken, vonyminbisymax.Mitwidthkann man angeben, wie breit die “Whisker” sein sollen.Um den Mittelwert zu verwenden, habe ich auch
geom_errorbarverwendet, aber füryminundymaxdenselben Wert angegeben, so dass die beiden Whisker übereinander liegen und nur ein Strichy gzeichnet wird.
Fehlerbalken
Fehlerbalken findet man oft in Plots. Leider hersscht keine Einigkeit darüber, was sie darstellen.
Meist zeigen sie an
die Standardabweichung der Einzelwerte,
den Standardfehler des Mittelwerts der Einzelwerte oder
das 95%-Konfidenzintervall des Mittelwerts der Einzelwerte.
Wenn man Fehlerbalken verwendet, muss man daher stets im Text klarstellen, was sie darstellen.
Das Zwiebel-Experiment vielfach wiederholt
Wenn wir das Experiment nun sehr oft wiederholen würden, wie oft geschieht es, dass sich die Konfidenzintervalle überlappen?
Dazu schreiben wir uns Code, der beide Konfidenzintervalle, zusammen mit beiden Mittelwerten, in eine Zeile schreibt:
tres_control <- t.test( onions_control )
tres_treated <- t.test( onions_treated )
result <- c(
control_mean = unname(tres_control$estimate),
control_ci_lower = tres_control$conf.int[1],
control_ci_upper = tres_control$conf.int[2],
treated_mean = unname(tres_treated$estimate),
treated_ci_lower = tres_treated$conf.int[1],
treated_ci_upper = tres_treated$conf.int[2]
)
result control_mean control_ci_lower control_ci_upper treated_mean
78.34088 72.38311 84.29864 89.37573
treated_ci_lower treated_ci_upper
80.86784 97.88361 Hier habe ich mittels c eine Vektor zusammen gebaut, der die 6 Werte enthält, die uns interessieren. Dabei habe ich ein Feature von c verwendet, dass wir bisher nicht kannten: Man kann jedem Wert einen “Namen” geben, so dass man auf den Wert danach auf zwei Wege zugreifen kann:
result[1]control_mean
78.34088 result["control_mean"]control_mean
78.34088 Allerdings hatte t.test selbst auch schon solche Namen vergeben, die ich oben mit unname entfernt habe, um nur meine eigenen Namen zu erhalten.
Das war alles vielleicht etwas umständlich, hilft uns aber gleich, den Überblick zu bewahren.
Wir erstellen eine Funtktion, die die Schritte von oben alle zusammen fasst. Die Funktion hat zwei Parameter: - die Anzahl \(n\) der Zwiebeln, die pro Feld geerntet werden (bisher stets 10) - die Wirkung des Düngers, gegeben als die Massenzunahme delta_m, die im Mittel pro Zwiebel erwartet wird (bisher stets 8 g)
onion_experiment <- function( n, delta_m ) {
# Ernte die Zwiebeln (Ziehe die Zufalslzahlen):
onions_control <- rnorm( n, mean=80, sd=9 )
onions_treated <- rnorm( n, mean=80 + delta_m, sd=9 )
# Berechne Mittelwerte und Konfidenzintervalle
tres_control <- t.test( onions_control )
tres_treated <- t.test( onions_treated )
# Stelle Ergebnis-Vektor zusammen:
c(
control_mean = unname(tres_control$estimate),
control_ci_lower = tres_control$conf.int[1],
control_ci_upper = tres_control$conf.int[2],
treated_mean = unname(tres_treated$estimate),
treated_ci_lower = tres_treated$conf.int[1],
treated_ci_upper = tres_treated$conf.int[2]
)
}
onion_experiment( 10, 8 ) control_mean control_ci_lower control_ci_upper treated_mean
80.18221 73.40883 86.95559 87.62455
treated_ci_lower treated_ci_upper
81.83594 93.41316 Nun können wir dies bequem 20 mal aufrufen:
replicate( 20, onion_experiment( n=10, delta_m=8 ) ) [,1] [,2] [,3] [,4] [,5] [,6] [,7]
control_mean 81.97020 80.17868 81.51667 83.66523 82.13535 82.80231 82.39239
control_ci_lower 74.68185 74.80203 75.49908 78.12771 78.43117 78.11090 77.18786
control_ci_upper 89.25854 85.55533 87.53425 89.20276 85.83953 87.49372 87.59691
treated_mean 89.55362 91.95552 87.09233 87.44592 89.05206 90.18091 87.25756
treated_ci_lower 84.65536 87.72651 80.42217 85.36274 82.90946 86.91722 83.45711
treated_ci_upper 94.45187 96.18453 93.76250 89.52909 95.19466 93.44460 91.05802
[,8] [,9] [,10] [,11] [,12] [,13] [,14]
control_mean 73.22046 83.27178 83.68770 80.43202 76.41051 77.01722 81.15025
control_ci_lower 66.45190 76.35056 75.79994 76.20228 67.62485 72.20400 76.87473
control_ci_upper 79.98903 90.19300 91.57546 84.66176 85.19617 81.83044 85.42577
treated_mean 89.01975 89.46486 88.57651 91.20462 86.31380 84.69914 84.49447
treated_ci_lower 85.49772 84.00958 83.50598 84.68831 77.73248 78.04531 75.98363
treated_ci_upper 92.54178 94.92014 93.64704 97.72092 94.89512 91.35298 93.00531
[,15] [,16] [,17] [,18] [,19] [,20]
control_mean 81.70982 82.74896 82.99320 79.14153 77.88347 76.14807
control_ci_lower 72.16598 76.89863 74.80970 71.70297 70.60807 71.56248
control_ci_upper 91.25366 88.59930 91.17671 86.58008 85.15887 80.73365
treated_mean 85.28769 87.45015 86.33396 83.41298 89.15954 82.16831
treated_ci_lower 78.22122 77.90502 79.11044 79.10842 81.38649 75.66498
treated_ci_upper 92.35416 96.99529 93.55748 87.71755 96.93259 88.67163Leider hat replicate die Angewohnheit, repolicate hat uns die 20 Ergebnis-Vektoren zu einer Matrix zusammen gestellt, aber leider mit jedem Experiment in eienr Spalte, statt in einer Zeile, wie wir es gewohnt sind. Wir benutzen die Funktion t (für “transpose”), die die Matrix transponiert, d.h., Zeilen und Spalten tauscht, und wandeln dann die Matrix in eine TIdyverse-Tabelle um:
replicate( 20, onion_experiment( n=10, delta_m=8 ) ) %>%
t() %>% as_tibble()# A tibble: 20 × 6
control_mean control_ci_lower control_ci_upper treated_mean treated_ci_lower
<dbl> <dbl> <dbl> <dbl> <dbl>
1 81.7 78.1 85.2 89.3 81.7
2 71.7 67.8 75.5 88.9 81.0
3 80.7 76.6 84.7 86.6 81.1
4 82.1 74.6 89.6 82.2 75.4
5 73.4 67.1 79.8 86.4 78.4
6 81.0 74.5 87.5 86.4 82.5
7 88.5 79.7 97.3 88.0 80.7
8 83.3 77.2 89.4 84.6 78.3
9 82.9 78.0 87.7 88.0 79.7
10 79.4 69.0 89.7 88.3 81.4
11 74.8 69.5 80.1 87.3 80.1
12 79.1 75.8 82.3 87.3 80.4
13 75.9 66.3 85.5 86.4 80.7
14 79.9 72.2 87.6 87.4 80.2
15 76.4 71.2 81.7 85.0 80.2
16 83.6 76.8 90.4 89.5 81.8
17 80.2 72.7 87.6 89.4 82.8
18 82.2 76.3 88.1 88.1 82.3
19 78.7 72.8 84.6 86.2 80.3
20 80.8 76.8 84.7 87.5 81.0
# ℹ 1 more variable: treated_ci_upper <dbl>Das das etwas umständlich war, leigt daran, dass replicate “altes R” ist. Die “moderne” Schreibweise ist
map_dfr( 1:20, ~ onion_experiment( n=10, delta_m=8 ) )# A tibble: 20 × 6
control_mean control_ci_lower control_ci_upper treated_mean treated_ci_lower
<dbl> <dbl> <dbl> <dbl> <dbl>
1 80.0 73.3 86.7 91.4 83.9
2 79.1 74.3 83.9 88.1 84.3
3 78.9 71.7 86.1 83.3 76.7
4 80.1 74.7 85.6 84.9 77.6
5 80.7 76.4 84.9 90.8 86.4
6 83.2 77.2 89.3 82.8 74.8
7 77.8 71.6 84.0 87.9 81.7
8 81.2 76.1 86.3 82.1 76.6
9 79.8 70.0 89.7 84.8 79.9
10 87.9 80.2 95.6 89.3 83.4
11 78.9 72.0 85.8 87.7 82.5
12 77.8 71.3 84.2 90.2 84.5
13 84.2 77.4 90.9 86.1 79.4
14 82.8 76.2 89.3 83.8 75.0
15 77.7 70.0 85.4 91.3 84.3
16 78.0 71.9 84.1 87.3 81.4
17 83.3 75.4 91.3 85.0 78.9
18 84.6 76.4 92.8 89.7 84.1
19 83.1 79.0 87.3 85.7 79.8
20 79.8 74.6 85.1 92.8 89.8
# ℹ 1 more variable: treated_ci_upper <dbl>Die Tidyverse-Funktionmap_dfr kann immer verwendet werden, wenn die inner Funktion (hier onion_experiment) einen vektor zurückgibt. Die Vektoren der einzelnen Durchläufe verwendet map_dfr dann als Zeilen, um daraus eine Tabelle zusammen zu setzen. (Die map functionen haben noch einige weiter wichtige Fähigkeiten, die wir ein anderes Mal behandeln.)
Hier ist ein versuch, die Tabelle graphisch darzustellen:
map_dfr( 1:20, ~ onion_experiment( n=10, delta_m=8 ) ) %>%
mutate( run = row_number() ) %>%
ggplot() +
geom_segment( aes( x=control_ci_lower, xend=control_ci_upper, y=run-.1, yend=run-.1 ), col="brown" ) +
geom_segment( aes( x=treated_ci_lower, xend=treated_ci_upper, y=run+.1, yend=run+.1 ), col="darkorange2" ) +
geom_point( aes( x=control_mean, y=run-.1 ), col="brown" ) +
geom_point( aes( x=treated_mean, y=run+.1 ), col="orange" ) +
geom_vline( xintercept = 80, color="brown", lty="dotted" ) +
geom_vline( xintercept = 88, color="orange", lty="dotted" ) +
theme_minimal( ) + xlab("x") + ylab("")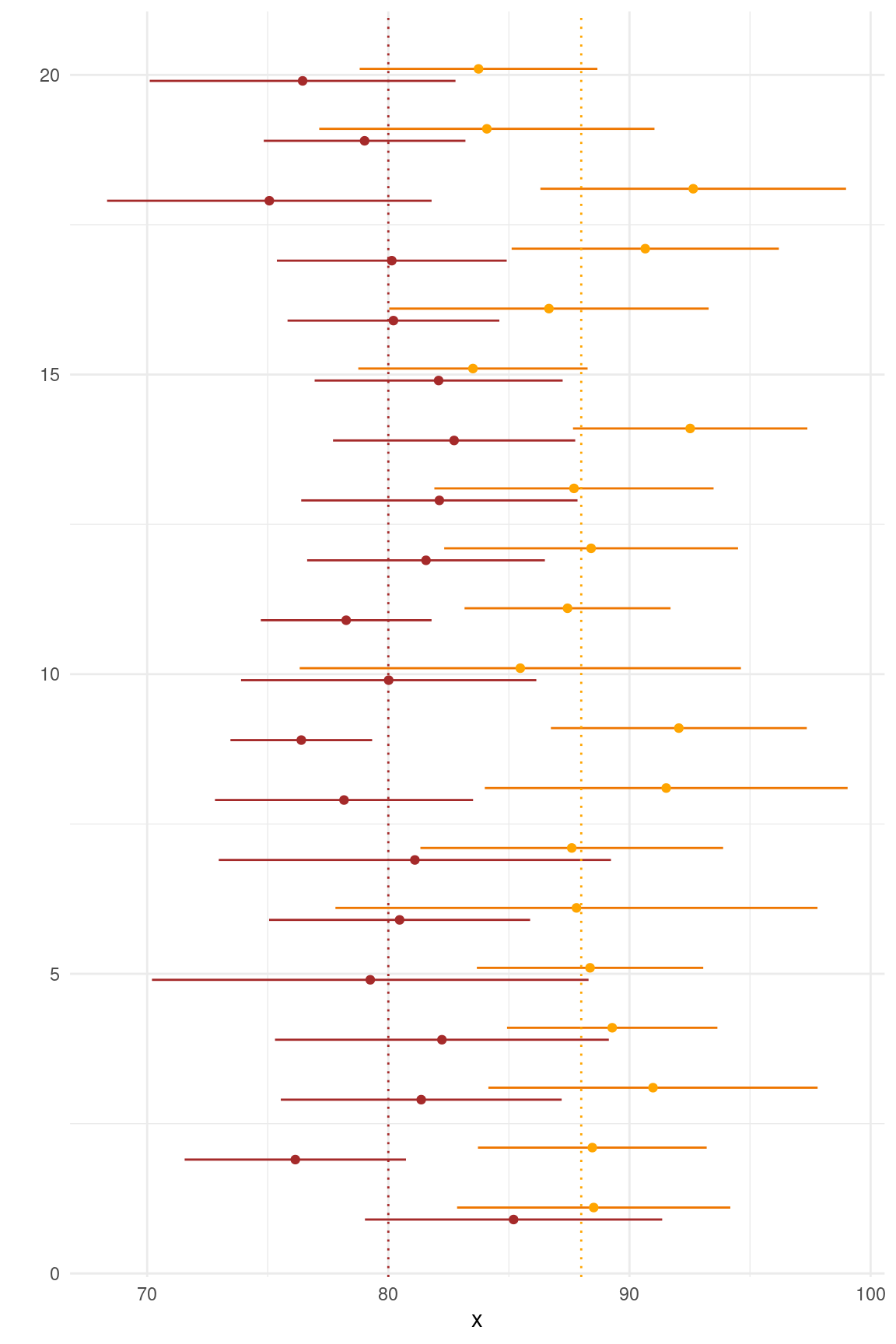
Nun können wir zählen, wie oft die Konfidenzintervalle von control und treated überlappen, indem wir die Untergrenze von treated mit der Obergrenze von control vergleichen:
map_dfr( 1:20, ~ onion_experiment( n=10, delta_m=8 ) ) %>%
mutate( ci_overlap = control_ci_upper > treated_ci_lower ) # A tibble: 20 × 7
control_mean control_ci_lower control_ci_upper treated_mean treated_ci_lower
<dbl> <dbl> <dbl> <dbl> <dbl>
1 76.9 72.5 81.3 86.7 77.5
2 81.3 74.4 88.3 87.8 78.9
3 78.3 71.3 85.2 87.8 83.2
4 80.3 74.8 85.8 90.9 85.4
5 82.6 77.2 88.0 86.7 83.0
6 76.3 70.4 82.3 92.5 87.7
7 79.6 73.4 85.8 91.4 87.4
8 79.3 72.4 86.2 90.5 86.4
9 76.9 71.6 82.3 86.9 81.2
10 81.4 73.9 88.9 83.7 77.4
11 78.0 73.7 82.4 93.2 87.2
12 80.8 75.6 85.9 89.5 84.3
13 82.9 78.7 87.2 87.2 81.6
14 78.9 74.3 83.5 81.6 75.9
15 76.1 70.9 81.3 91.2 83.5
16 81.0 77.4 84.6 86.3 82.4
17 82.5 75.4 89.6 90.5 81.8
18 80.6 73.2 88.1 86.1 80.3
19 77.6 69.5 85.6 91.5 84.3
20 83.1 76.7 89.6 86.7 81.6
# ℹ 2 more variables: treated_ci_upper <dbl>, ci_overlap <lgl>Dies machen wir jetzt 10000 mal (statt nur 20 mal) und zählen:
map_dfr( 1:10000, ~ onion_experiment( n=10, delta_m=8 ) ) %>%
mutate( ci_overlap = control_ci_upper > treated_ci_lower ) %>%
group_by( ci_overlap ) %>%
summarise( n() )# A tibble: 2 × 2
ci_overlap `n()`
<lgl> <int>
1 FALSE 1644
2 TRUE 8356Wie sehen: Die Konfidenzintervalle überlappen mit Wahrscheinlichkeit 84%. Bei diesem Experiment besteht also nur eine Wahrscheinlichkeit von 16%, dass der Dünger uns von seiner Wirksamkeit überzeugen kann.
Nur zur Erinnerung: Wir können den Code aus dem vorstehendem Chunk auch folgendermaßen schreiben, und erhalten direkt den Anteil der Durchgänge ohne Überlapp:
map_dfr( 1:10000, ~ onion_experiment( n=10, delta_m=8 ) ) %>%
mutate( ci_overlap = control_ci_upper > treated_ci_lower ) %>%
summarise( mean( !ci_overlap ) )# A tibble: 1 × 1
`mean(!ci_overlap)`
<dbl>
1 0.160Statistical Power
Was wir eben durchgeführt haben, nennt man eine “Power Calculation”. So etwas wichtig ist, wenn Sie ein Experiment planen.
Wir haben hier das folgende experimentelle Design (auch “Versuchsplan” genannt) gewählt: Ein Feld wird gedüngt, eines nicht. Von jedem Feld werden \(n\) Zwiebeln geerntet.
Ausserdem haben wir als Teil unseres Versuchsplans folgende Entscheidungsregel vorab festgelegt: Wenn das 95%-Konfidenzintervalle für die behandelte Stichprobe vollständig, also ohne Überlapp, über dem 95%-KI der Vergleichs-Probe liegt, dann (und nur dann) werden wir folgern, dass der Dünger wirkt.
Nun fragen wir uns: Wie wahrscheinlich ist es, dass der Dünger uns überzeugen kann, wenn
die wahre Wirkung des Düngers eine Erhöhung der Zwiebel-Masse um (im Mittel) 8 g ist,
die Masse von Zwiebeln unserer Sorte eine Standardabweichung von 8 g um ihren Mittelwert bildet?
Wie wir gesehen haben, ist unter diesen Annahmen die statistische Power unseres Versuchsplans –also die Wahrscheinlichkeit, dass wir zu einem positivem Ergebnis kommen– nur 16%.
Wie wäre es, wenn wir den Stichproben-Umfang pro Feld von 10 auf 30 erhöhen?
map_dfr( 1:10000, ~ onion_experiment( n=30, delta_m=8 ) ) %>%
mutate( ci_overlap = control_ci_upper > treated_ci_lower ) %>%
summarise( mean( !ci_overlap ) )# A tibble: 1 × 1
`mean(!ci_overlap)`
<dbl>
1 0.712Mit \(n=30\) swtatt \(n=10\) steigt unsere Power von 10% auf etwa 70%.
Und wie wäre es, wenn wir bei 10 Zwiebeln pro Feld bleiben, aber optimistischer darin sind, wie gut der Dünger wirkt? Nehmen wir an, der Dünger erhöhe die Zwiebel-Masse im Mittel um 15 g:
map_dfr( 1:10000, ~ onion_experiment( n=10, delta_m=15 ) ) %>%
mutate( ci_overlap = control_ci_upper > treated_ci_lower ) %>%
summarise( mean( !ci_overlap ) )# A tibble: 1 × 1
`mean(!ci_overlap)`
<dbl>
1 0.705Zusammengefasung
Wenn man ein Experiment plant, kann es sehr hilfreich sein, Simulationen wie eben gezeigt durchzuführen. Wir gehen dabei wie folgt vor:
Wir erstellen einen Versuchsplan und legen eine Entscheidungsregel fest.
Wie machen Annahmen darüber, wie die wahre Verteilung aussehen könnte, die unseren Messwerten zugrunde liegt.
Wir schreiben Code, der
- mit Hilfe von Zufallszahlen simulierte Messwerte gemäß unserer Annahmen generiert, und
- diese Messwerte anhand unserer Entscheidungsregel auswertet
Wir lassen den Code mehrere tausend Mal laufen und zählen, wie oft unsere Entscheidungsregel ein positives Ergebnis liefert.
So können wir die statistische Power unseres Versuchsplans (zusammen mit unserer Entscheidungsregel) ermitteln, also die Wahrscheinlichkeit, ein positives Ergebnis zu bekommen und somit mit dem Versuch einen Erfolg zu erzielen.
Wichtig: Eine negative Antwort der Entscheidungsregel ist hier kein Erfolg, denn es gibt nicht die Antwort “Nein, es gibt keinen Effekt”, sondern als die Antwort “Wir können nicht sagen, ob es einen Effekt gibt”. Das wird klar, wenn Sie daran denken, dass unsere Entscheidungsregel in der Simulation ein negative Ergebnis liefern kann, obwohl wir ja den fall simulieren, dass es einen wahren Effekt gibt!
Wenn uns die statistische Power zu gering erscheint, haben wir drei Möglichkeiten:
Größere Stichprobe
Wir können den Stichproben-Umfang erhöhen und die Simulation wiederholen. So finden wie wir heraus, wie groß der Stichprobenumfang mindestens sein muss, um gute Erfolgs-Chancen zu haben.
Aber: Wir könnten zum Ergebnis kommen, dass wir mehr den Stichproben-Umfang so extrem erhöhen müssen, dass das Experiment mit den vorhandenen Resourcen schlicht nicht durchführbar ist.
So ein Ergebnis muss man ernst nehmen! Einfach trotzdem mit zu kleinem Stichproben-Umfang weiter zu machen, hat schon viele Forschngsprojekte ruiniert.
Optimistischere Annahmen zur Effektstärke
Wir können unsere Annahmen überprüfen. Vielleicht waren wir bei unserer Schätzung zur Effektgröße (effect strength, bei uns: Massenzunahme pro Zwiebel) zu pessimistisch.
Aber: Hüten Sie sich hier von falschem Optimismus und Wunschdenken (“wishful thinking”)! Das hat schon oft zu Misserfolgen mit großer Verschwendung von Geld und Zeit geführt, und kann
Versuchsplan ändern
Wir soltlen auch Versuchsplan und Entscheidungsregel überprüfen: Manchmal kömnnen Verbesserungen hier den entscheidenden Unterschied machen. Hierzu ist aber statistische Expertise wichtig, weswegen man spätestens jetzt als Laborbiologe ohne weitergehende Statistik-Kenntnisse einen Statistiker um Rat fragen sollte.
Die/Den Statistiker/in erst um Rat zu fragen, wenn das Experiment bereits durch geführt wurde, ist eine (leider viel zuhäufige) Todsünde in der experimentellen Forschung.
“To consult the statistician after an experiment is finished is often merely to ask him to conduct a post mortem examination. He can perhaps say what the experiment died of.” – R. A. Fisher
Zielsetzung ändern
Wenn die Power-Calculation ergibt, dass ihr geplantes Experiment nicht durchführbar ist, auch nicht, wenn Sie Versuchsplan und Auswertung optimieren, bleibt nur eins: Geben Sie dieses Ziel auf und suchen Sie sich ein anderes!
Konfidenz-Intervall von Differenzen und der t-Test
ZUrück zu Student’s t-Verteilung uns seinem t-Test.
Betrachten wir nochmal unser Zwiebel-Experiment:
set.seed( 13245768 )
onions_control <- rnorm( 10, mean=80, sd=9 )
onions_treated <- rnorm( 10, mean=88, sd=9 )
t.test( onions_control )$conf.int[1] 72.38311 84.29864
attr(,"conf.level")
[1] 0.95t.test( onions_treated )$conf.int[1] 80.86784 97.88361
attr(,"conf.level")
[1] 0.95Eigentlich interessieren uns die Mittelwerte der beiden Stichproben nicht direkt. Was uns wirklich interessiert, ist ihre Differenz: Ist der Mittelwert der gedüngten Zwiebeln höher als der der der unbehandelten?
mean( onions_treated ) - mean( onions_control )[1] 11.03485Wenn wir ein 95%-KI für diese Differenz hätten, dann könnten wir fragen, ob es über seine ganze Spanne gröser als 0 ist, oder ob er die Null überlappt. In ersterem Fall hätten wir 95% Konfidenz dafür, dass der Dünger die Zwiebelmasse wirklich erhöht.
Die t.test-Funktion hilft uns hier weiter:
Wenn man der t.test-Funktion zwei Vektoren gibt (statt nur einen wie bisher), dann berechnet sie die Mittelwerte der beiden Vektoren sowie das Konfidenzintervall der Differenz der beiden Mittelwerte, nicht mehr das KI der Mittelwerte selbst:
t.test( onions_treated, onions_control )
Welch Two Sample t-test
data: onions_treated and onions_control
t = 2.4034, df = 16.116, p-value = 0.02863
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
1.307174 20.762525
sample estimates:
mean of x mean of y
89.37573 78.34088 Wie sehen, dass das KI die Null nicht überlappt. Beide Grenzen sind rechts der Null. Also dürfen wir mit 95% Konfidenz sagen, dass der Dünger eine Wirkung hat.
Das mag erstaunen, denn die KIs der Einzelwerte haben überlappt. Es ist aber korrekt: Konfidenzintervalle von Differenzen sind stets kürzer als die Summe der Konfidenzintervalle der Werte, die voneinander subtrahiert werden.
Konfidenzintervall der DIfferenz, von Hand berechnet
Wir können das auch “per Hand” berechnen:
Die Standardfehler der beiden Mittelwerte sind:
sem_control <- sd( onions_control ) / sqrt( length(onions_control) )
sem_control[1] 2.633667sem_treated <- sd( onions_treated ) / sqrt( length(onions_treated) )
sem_treated[1] 3.76096Vermutlich kennen Sie die folgende Regel zur “Fehlerrechnung”: Wenn man zwei Werte, die mit Standardfehlern assoziert sind, addiert oder voneinander abzieht, ist das Quadrat des Standardfehlers der Summe/Differenz die Summe der Quadrate der Standardfehler der beiden Werte: sem_differenz^2 = sem_control^2 + sem_treated_2.
(Grund: Das Quadrieren verwandelt die Standardabweichungen in Varianzen, und Varianzen sind additiv.)
Also:
sem_difference = sqrt( sem_control^2 + sem_treated^2 )
sem_difference[1] 4.591407Um ein 95%-KI zu erhalten, müssen wir den Student-Faktor bestimmen:
sf <- qt( 0.975, 9 )difference <- mean(onions_treated) - mean(onions_control)
sf <- qt( 0.975, 9 )
c( difference - sf * sem_difference, difference + sf * sem_difference )[1] 0.6483652 21.4213334Dies ist allerdings nicht ganz derselbe Wert, den auch t.test liefert:
t.test( onions_treated, onions_control )
Welch Two Sample t-test
data: onions_treated and onions_control
t = 2.4034, df = 16.116, p-value = 0.02863
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
1.307174 20.762525
sample estimates:
mean of x mean of y
89.37573 78.34088 Der Unterschied rührt daher, dass wir unseren Student-Faktor mit 9 Freiheitsgraden berechnet haben, weil wir unseren Standardfehler aus 10 Werten berechnet haben (10-1=9). Student und Welch haben erkannt, dass man bei einer Differenz zwischen zwei Größen mehr Freiheitsgrade ansetzten darf als bei den Einzelwerten, weil sich die Abweichungen der Einzelwerte von ihren jeweiligen wahren Werten beim Differenzbilden gegenseitig kompensieren können. Hier hat t.test daher die Anzahl der Freiheitsgrade von 9 auf 16.1 erhöht, was den STudent-Faktor verringert und somit unser Konfidenzinterval schmäler gemacht hat. Den Wert 16.1 hat R mit Hilfe eine Formel bestimmt, die von B. L. Welch stammt, weswegen die Ausgabe mit “Welch’s t test” (statt “Student’s t-test”) überschrieben ist. Die Formel finden Sie im Wikipedia-Artikel zu Welch’s t-Test.
Differenz mit gleicher Varianz
Student’s ursprüngliche Lösung war, anzunehmen, dass bei beiden Stichproben die wahre Standardabweichung dieselbe ist. Das ist bei uns auch in der Tat der Fall: wir haben ja auch angenommen, dass der Dünger nur den Erwartungswert um 8 g erhöht, die Standardabweichung von 9 g sich aber nicht ändert. Diese Annahme ermöglicht es, für beide Stichproben einen gemeinsamen Wert für den Standardfehler zu ermitteln.
Dazu bestimmt man zunächst die sog. “gepoolte Stichprobenvarianz”, für die die normale Formel für die Stichproben-Varianz etwas abwandelt wird: Man nimmt die Einzelwerte beider Stichproben zusammen, zieht von jedem Einzelwert den jeweils zugehörigen Mittelwert ab, quadriert diese Abweichungen, summiert sie und teilt die Summe dann nicht, wie sonst, durch die \(n-1\) (wobei \(n\) die Anzahl der Einzelwerte in beiden Stichproben zusammen ist, bei uns also 20), sondern durch \(n-2\), da 2 Mittelwerte vorkamen. Dies teilt man durch \(\sqrt{n}\), um den “gepoolten Standardfehler” (pooled SEM zu erhalten). Diese Details müssen Sie sich nicht merken, Sie können Sie bei Bedarf z.B. hier auf Wikipedia nachlesen.
Wir machen das einmal per Hand – auch wenn wir in der Praxis diese mühsame Rechnung der t.test-Funktion überlassen.
pooled_sd <-
sqrt( sum(
c( ( onions_control - mean(onions_control) )^2,
( onions_treated - mean(onions_treated) )^2 ) ) / 18 )Damit haben beide Mittelwerte den geschätzten Standardfehler
sem_pooled <- pooled_sd / sqrt(10)
sem_pooled[1] 3.246615Also ist der Standardfehler der Differenz
sem_diff <- sqrt( sem_pooled^2 + sem_pooled^2 )
sem_diff[1] 4.591407Nun berechnen wir den Student-Faktor. Diesmal haben wir 18 Freiheitsgrade, denn der Standardfehler wurde aus 20 Einzelwerten, minus zwei Mittelwerten, berechnet:
sf <- qt( .975, 18 )Also beträgt das Konfidenz-Interval der Differenz bei Annahme gleicher Varianz in beiden Stichproben
c( difference - sf * sem_diff, difference + sf * sem_diff )[1] 1.388661 20.681037Wenn wir t.test mitteilen, dass es dieselbe Annahme machen sollen (indem wir var.equal=TRUE setzen), so erhalten wir genau dasselbe Konfidenz-Intervall:
t.test( onions_treated, onions_control, var.equal=TRUE )
Two Sample t-test
data: onions_treated and onions_control
t = 2.4034, df = 18, p-value = 0.02724
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
1.388661 20.681037
sample estimates:
mean of x mean of y
89.37573 78.34088 Da wir nun gesehen haben, dass t.test das Konfidenzintervall einer Differenz zweier Mittelwerte berechnen kann, können Sie sich nun nur dies merken und alle mathematschen Details wieder vergessen.
Zusammenfasung
Oft interessiert man sich für die Differenz zweier Mittelwerte.
Meist geht es um die Differenz zwischen dem Mittelwert einer behandelten Stichprobe (treated sample) und einer Vergleichs-Stichprobe (control sample).
Hier interessiert uns ob die Differenz “statistisch signifikant” von Null abweicht, denn dann können wir auf dem zugehörigen Konfidenz-Niveau folgern, dass die Behandlung wirklich einen Effekt hatte.
Dazu berechnen wir ein Konfidenz-Intervall für die Differenz zu einem gegebenen Konfidenz-Niveau (confidence level, z.B. 95%).
Hierzu verwenden wir die Funktion
t.test, der wie die beiden Vektoren mit den Einzelwerten der behandelten und der unbehandelten Stichprobe als erstes und zweites Argument übergeben.Die Funktion gibt uns dann ein 95%-Konfidenz-Intervall für die Differenz aus (da wir bei Bedarf mit
t.test(...)$conf.intextrahieren können).Wenn wir ein anderes Konfidenz-Niveau als 95% wünschen, übergeben wir
t.testden optionalen Parameterconf.level, z.B.t.test( ...., conf.level=.99 ).Wenn wir guten Grund zur Annahme haben, dass die wahre Varianz durch die Behandlung nicht beeinflusst wird, dann dürfen wir das Zusatz-Argument
var.equal=TRUEverwenden. Es erhöht die statistische Power, d.h., das Konfidenz-Intervall wird dadurch schmäler.Der t-Test mit
var.equal=TRUEist der ursprüngliche “Students t-Test”, wie ihn Student/Gosset vorgeschlagen hat. Wenn man die Option weglässt, nimmtt.testvar.equal=FALSEand und führt die Variante des t-Tests durch, die diese Annahme nicht verwendet. Sie wird in der Literatur als “Welch’s t-Test” bezeichnent.
Einschub zur Terminologie: Oben habe ich geschrieben: “Meist geht es um die Differenz zwischen dem Mittelwert einer behandelten Stichprobe (treated sample) und einer Vergleichs-Stichprobe (control sample).” Hier unterscheidet sich die Verwendung des Wortes “sample” zwischen den Disziplinen: Statistiker sagen: “The treatment sample comprises 10 onions”, d.h. alle Zwiebeln zusammen sind eine Stichprobe. Biologen und Mediziner sagen gerne: “This onion is a sample from the treated field.”, d.h. jede einzelne Zwiebel ist eine Probe. Im Deutschen löst sich das Problem, da Statistiker das Wort “Stichprobe” verwenden, Biologen und Mediziner aber nur “Probe” sagen.
Interpretation des t-Test-Ergebnisses
Wenn das Konfidenzintervall die Null überdeckt, können wir nicht mit der gewünschten Konfidenz sagen, ob die Behandlung der behandelten Stichprobe irgendeine Wirkung hatte. Wir können also die Nullhypothese (null hypothesis), dass die Behandlung keinerlei Einfluss (no effect) auf die Messwerte hat, nicht verwerfen.
Wenn das Konfidenzintervall hingegen die Null nicht überlappt, können wir diese Nullhypothese verwerfen (reject the null hypothesis). Wir dürfen also sagen: Der Behandlung hatte vermutlich eine Wirkung.
Beispiel: Die Differenz in unserem Zwiebel-Beispiel beträgt die Differenz der Stichproben-Mittelwerte 6 g, ihr 95%-KI geht von 1 g bis 11 g.
Richtig: “Auf einem Konfidenzniveau von 95% können wir ausschließen, dass der Dünger völlig wirkungslos ist.”
Falsch: “Mit einem Konfidenzniveau von 95% können wir sagen, dass der Dünger wirkt; die Wirkung ist eine Erhöhung der Zwiebelmasse um durchschnittlich 6 g.”
Richtig: “Mit einem Konfidenzniveau von 95% können wir sagen, dass der Dünger wirkt und die Wirkung eine Erhöhung der mittleren Zwiebelmasse um mindestens 1 g ist.”
Die falsche Formulierung ist leider die, die die meisten Experimentatoren verwenden.
p-Werte
Betrachten wir nochmals die Ausgabe des t-Tests, diesmal mit Stichproben zu je 50 Zwiebeln:
set.seed( 13245768 )
onions_control <- rnorm( 30, mean=80, sd=9 )
onions_treated <- rnorm( 30, mean=88, sd=9 )
t.test( onions_treated, onions_control )
Welch Two Sample t-test
data: onions_treated and onions_control
t = 3.4322, df = 55.525, p-value = 0.001138
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
3.250239 12.367236
sample estimates:
mean of x mean of y
88.23206 80.42332 Angenommen, es ginge uns nur darum, zu wissen ob der Dünger irgendeine Wirkung hat. Wie stark die Wirkung ist, ist uns völlig egal. Die Aussage “Der Dünger hat eine Wirkung” können wir mit mehr Konfidenz machen als 95%, denn wenn wir t.test bitten, uns ein 99%-Konfidenzintervall zu bestimmen, überlappt auch dieses die Null nicht:
t.test( onions_treated, onions_control, conf.level=0.99 )
Welch Two Sample t-test
data: onions_treated and onions_control
t = 3.4322, df = 55.525, p-value = 0.001138
alternative hypothesis: true difference in means is not equal to 0
99 percent confidence interval:
1.740245 13.877230
sample estimates:
mean of x mean of y
88.23206 80.42332 Wenn ich aber ein 99,9%-Intervall fordere, verlange ich zu viel:
t.test( onions_treated, onions_control, conf.level=0.999 )$conf.int[1] -0.09633467 15.71380985
attr(,"conf.level")
[1] 0.999Wo genau liegt die Grenze?
Ich könnte probieren, aber t.test hat die Grenze bereits ausgerechnet. Es ist der p-Wert: in der Ausgabe von t.test steht: p-value = 0.001138. Noch genauer:
pvalue <- t.test( onions_treated, onions_control )$p.value
pvalue[1] 0.001137678Wir berechnen das Komplement zu 100%, und fordern also ein 99,886%-Konfidenzintervall:
t.test( onions_treated, onions_control, conf.level=1-pvalue )$conf.int[1] 4.041446e-15 1.561748e+01
attr(,"conf.level")
[1] 0.9988623Nun liegt die Untergrenze bei \(4\cdot 10^{-15}\), also bei Null. (Die Rechengenauigkeit von R liegt in etwa bei \(10^{-15}\).)
Wir erkennen: Der p-Wert, den uns ein t-Test liefert, gibt an, bei welchem Konfidenzniveau das Konfidenzintervall der Differenz die Null gerade berührt.
Bei diesem Konfidenz-Niveau können wir die Nullhypothese (“Der Dünger hat überhaupt keine Wirkung”) gerade noch ablehnen, aber keine Aussage mehr über die Stärke des Effekts machen.
Unser als “Richtig” markierte Satz von oben lautete also:
- “Mit einem Konfidenzniveau von 95% können wir sagen, dass der Dünger eine Wirkung auf die Zwiebeln hat und dass diese Wirkung eine Erhöhung der mittleren Zwiebelmasse um mindestens 3.25 g ist.”
und
- “Mit einem p-Wert von 0.11%, also einem Konfidenzniveau von 99,88%, können wir sagen, dass der Dünger eine Wirkung auf die Zwiebeln hat
und die Wirkung eine Erhöhung der mittleren Zwiebelmasse um mindestens 0 g ist.”
Der letzte Halbsatz ist gestrichen, nicht weil er falsch ist, sondern weil er inhaltsleer ist.
Wenn wir beide Sätze zusammenfassen möchten, sollten wir schreiben: “Mit einem p-Wert von 0.11% (also auf einem Konfidenzniveau von 99.88%) können wir sagen, dass der Dünger die mittlere Zwiebelmasse erhöht, und auf einem Konfidenzniveau von 95% können wir sagen, dass die Erhöhung der mittleren Zwiebelmasse mindestens 3.25 g aber nicht mehr als 12.38 g beträgt.”
All das können wir aus der Ausgabe von t.test bequem ablesen:
t.test( onions_treated, onions_control )
Welch Two Sample t-test
data: onions_treated and onions_control
t = 3.4322, df = 55.525, p-value = 0.001138
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
3.250239 12.367236
sample estimates:
mean of x mean of y
88.23206 80.42332 Nullhypthese und p-Wert
Unser Zwiebel-Experiment kann zwei verschiedene Zielsetzungen haben:
Quantitativ: Wir möchten herausfinden, wie gut der Dünger wirkt.
Qualitativ: Wir möchten herausfinden, ob der Dünger überhaupt irgendeinen Einfluss auf die Zwiebeln hat.
Für quantitative Fragestellungen sind Konfidenzintervalle hilfreich, für qualitative wird häufig der p-Wert bevorzugt.
Für letzteren stellt man eine sog. Null-Hypothese (null hypothesis) auf. In unserem Beispiel: Der Dünger hat keinerlei Einfluss auf die Zwiebelmasse. (Die durchschnittliche Erhöhung der Zwiebelmasse durch den Dünger ist also 0.)
Wir fragen: Erlauben uns die Daten, diese Nullhypothese zu verwerfen (reject the null hypothesis)?
Wir bestimmen die Differenz \(\Delta m\) zwischen den mittleren Zwiebelmassen in treated und control field und fragen: Wenn die Nullhypothese zuträfe, wenn der Dünger also keinen Einfluss auf die Zwiebelmasse hat, wie wahrscheinlich ist es, dass man dennnoch eine Differenz beobachtet, die mindestens \(\Delta m\) beträgt?
Diese Wahrscheinlichkeit hqngt natürlich von der Standardabweichung in den Stichproben ab, die wir ja auch schätzen. Daher teilen wir die Differenz durch Ihren Standardfehler, nennen diesen Quotienten \(t\) und fragen: Wie groß ist die Wahrscheinlichkeit, dass man in einem Experiment einen \(t\)-Wert erhält, der im Betrag mindestens so groß ist wir der beobachtete Werte?
Im folgenden führen wir diese Schritte in einem beispiel durch:
Wir erzeugen wieder zwei Ernten, und vergleichen per t-Test.
set.seed( 13245768 )
onions_control <- rnorm( 10, mean=80, sd=9 )
onions_treated <- rnorm( 10, mean=88, sd=9 )
t.test( onions_treated, onions_control, var.equal=TRUE )
Two Sample t-test
data: onions_treated and onions_control
t = 2.4034, df = 18, p-value = 0.02724
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
1.388661 20.681037
sample estimates:
mean of x mean of y
89.37573 78.34088 Nun berechnen wir den p-Wert “per Hand”, um zu sehen, was die t.test-Funktion gerechnet hat.
Dazu berechnen wir, wieder mit demselben Code wie oben, die gepoolte Standardabweichung der beiden Stichproben, und daraus den gemeinsamen (gepoolten) Standardfehler der beiden Mittelwerte
pooled_sd <-
sqrt( sum(
c( ( onions_control - mean(onions_control) )^2,
( onions_treated - mean(onions_treated) )^2 ) ) / 18 )
sem_pooled <- pooled_sd / sqrt(10)
sem_pooled[1] 3.246615Also ist der Standardfehler der Differenz (wieder derselbe Code wir oben)
se_diff <- sqrt( sem_pooled^2 + sem_pooled^2 )
se_diff[1] 4.591407Nun teilen wir die Differenz durch ihren Standardfehler:
t_value <- ( mean(onions_treated) - mean(onions_control) ) / se_diff
t_value[1] 2.40337Diesen Wert nennen wir den t-Wert:
\[t\text{-Wert} = \frac{\text{Differenz der Stichproben-Mittelwerte}}{\text{aus der Stichproben geschätzter Standardfehler dieser Differenz}}\] (Zur Erinnerung: Wenn wir den Nenner nicht als Schätzung, sondern als genauen Wert betrachten, nennen wir den Quotienten einen \(z\)-Wert.)
Unser \(t\)-Wert ist 2.4; unsere Differenz ist also das 2.4-fache ihres Standardfehlers.
Nehmen wir nun an, die Nullhypothese träfe zu: Der wahre Wert der Differenz wäre dann 0, und unser Wert weicht um das 2.4-fache ihres Standardfehlers von ihrem wahren Wert ab.
Wie wahrschinlich ist es, dass ein geschätzter Wert um das 2.4-fache seines Standardfehlers vom wahren Wert abweicht? Wenn man den STandardfehler exakt weiss, rechnet man:
2* ( 1 - pnorm(2.4) )[1] 0.01639507Da unser Standardfehler aus 18 Freiheitsgraden (20 Werte minus 2 Mittelwerte) geschätzt ist, verwenden wir stattd er Normalverteilung die t-Verteilung mit df=18:
2* ( 1 - pt( 2.4, 18 ) )[1] 0.02742687Wenn die Nullhypothese zuträfe, die wahre Differenz alson 0 wäre, wie wahrscheinlich wäre es dann, eine Differenz zu erhalten, die mehr \(t=2.4\) Standardfehler, oder noch mehr, vom wahren Wert 0 abweicht? – Die Antwort lautet \(p=0.0274\) und diesen Wert nennen wir den p-Wert des t-Tests.
Es ist auch tatsächlioch genau der Wert, den der Aufruf von t.test oben als p value geliefert hat.
Wir argumentieren nun: Wenn die Nullhypothese zuträfe, dann wäre es ziemlich unwahrscheinlich (nämlich nur 2.74% Wahrscheinlichkeit), dass wir eine Differenz zwischen gedüngtem und ungedüngten Mittelwert erhielten, die mindestens so groß ist wie die, die wir beobachtet haben. Also schließen wir, dass es unwahrscheinlich ist, dass die Nullhyopthese zutrifft und verwefen sie daher: Wir folgern, dass der Dünger tatsächlich einen Einfluss auf die Zwiebelmasse hat. Wir beziffern unsere “Konfidenz” (confidence) in diese Aussage mit \(1-0.0274=97.26\%\)
Bachten Sie: Das bedeutet nicht, dass die Aussage “Der Dünger wirkt” mit Wharscheinlichkeit 97.25% wahr wäre, oder mit Wahrscheinlichkeit 2,75% falsch.
Wir sagen lediglich: Ein Ergebnis, wie wir es beobachtet haben, oder ein noch stärkeres, wäre unwahrscheinlich (nur 2.74% Wahrscheinlichkeit), wenn die Null-Hypothese (“Dünger bewirkt nichts.”) zuträfe.
Der Unterschied zwischen diesen Formulierungen mag klein erscheine, ist aber wichtig. Den Unterschied zu erkennen, erfordert genaues Nachdenken!
Null-Simulationen
Abschließend lassen wir unsere onion_experiment-Funktion nochmals mehrmals laufen, simulieren diesmal aber die Nullhypothese, setzten also \(delta_m=0\):
map_dfr( 1:20, ~ onion_experiment( n=10, delta_m=0 ) ) %>%
mutate( run = row_number() ) %>%
ggplot() +
geom_segment( aes( x=control_ci_lower, xend=control_ci_upper, y=run-.1, yend=run-.1 ), col="brown" ) +
geom_segment( aes( x=treated_ci_lower, xend=treated_ci_upper, y=run+.1, yend=run+.1 ), col="darkorange2" ) +
geom_point( aes( x=control_mean, y=run-.1 ), col="brown" ) +
geom_point( aes( x=treated_mean, y=run+.1 ), col="orange" ) +
geom_vline( xintercept = 80, color="brown", lty="dotted" ) +
geom_vline( xintercept = 88, color="orange", lty="dotted" ) +
theme_minimal( ) + xlab("x") + ylab("")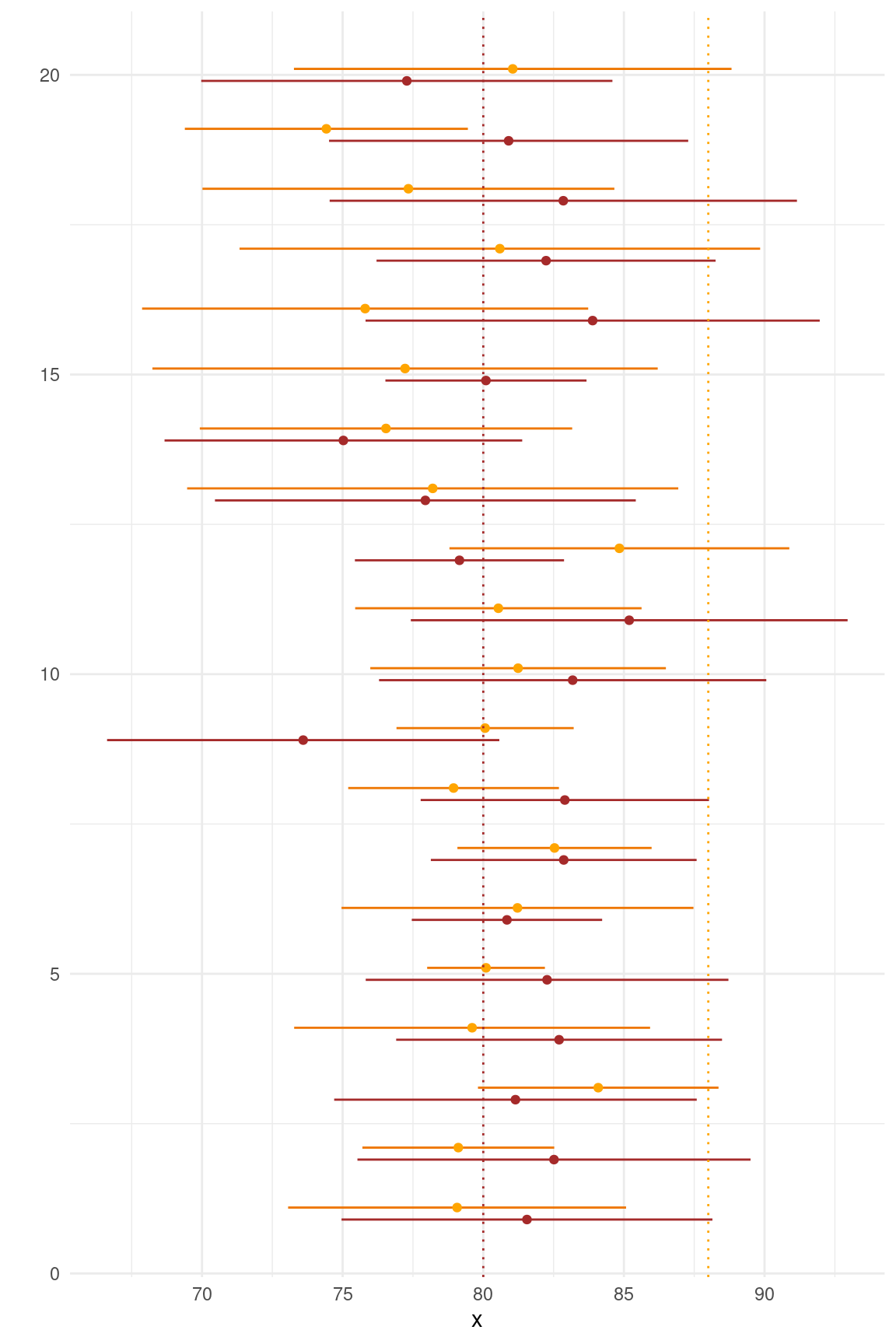
Wir können auch die 95%-Konfidenzintervalle der Differenzen 100-mal berechnen und plotten:
map_dfr( 1:100, ~ {
onions_control <- rnorm( 10, mean=80, sd=9 )
onions_treated <- rnorm( 10, mean=80, sd=9 )
t.test( onions_treated, onions_control )$conf.int %>%
set_names( "ci_lo", "ci_hi" ) } ) %>%
mutate( idx = row_number() ) %>%
ggplot +
geom_segment( aes( x=ci_lo, xend=ci_hi, y=idx, yend=idx ) ) +
geom_vline( xintercept = 0 )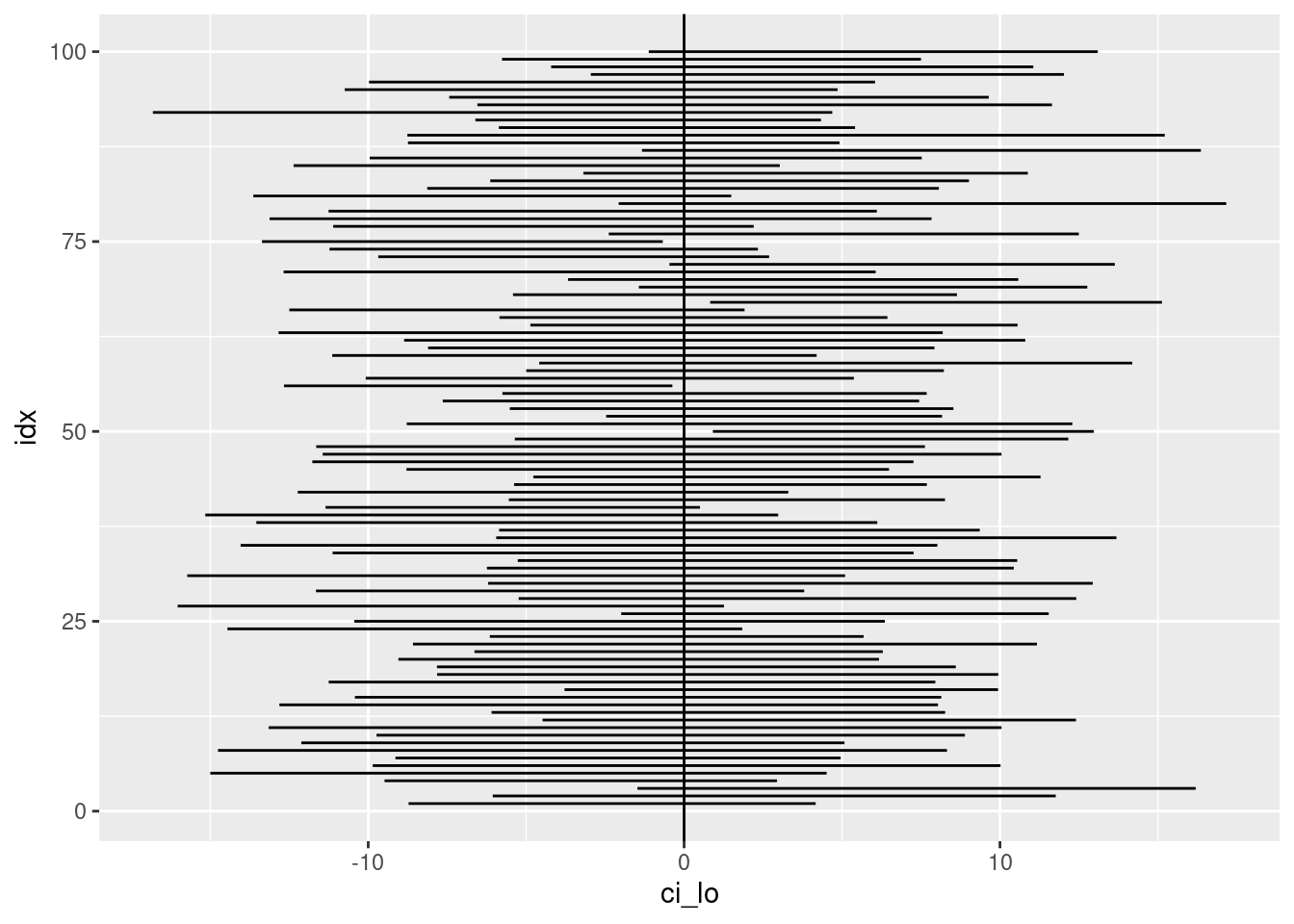
Wie wir sehen, überlappen 95% der 100 Konfidenzintervalle den wahren Wert der Differenz, also 0.
Interessant ist auch, den t-Test 1000-mal für die simulierte Nullhypothese durchzuführen und ein Histogramm der p-Werte zu erstellen:
replicate( 1000, {
onions_control <- rnorm( 10, mean=80, sd=9 )
onions_treated <- rnorm( 10, mean=80, sd=9 )
t.test( onions_treated, onions_control )$p.value
}) %>% hist()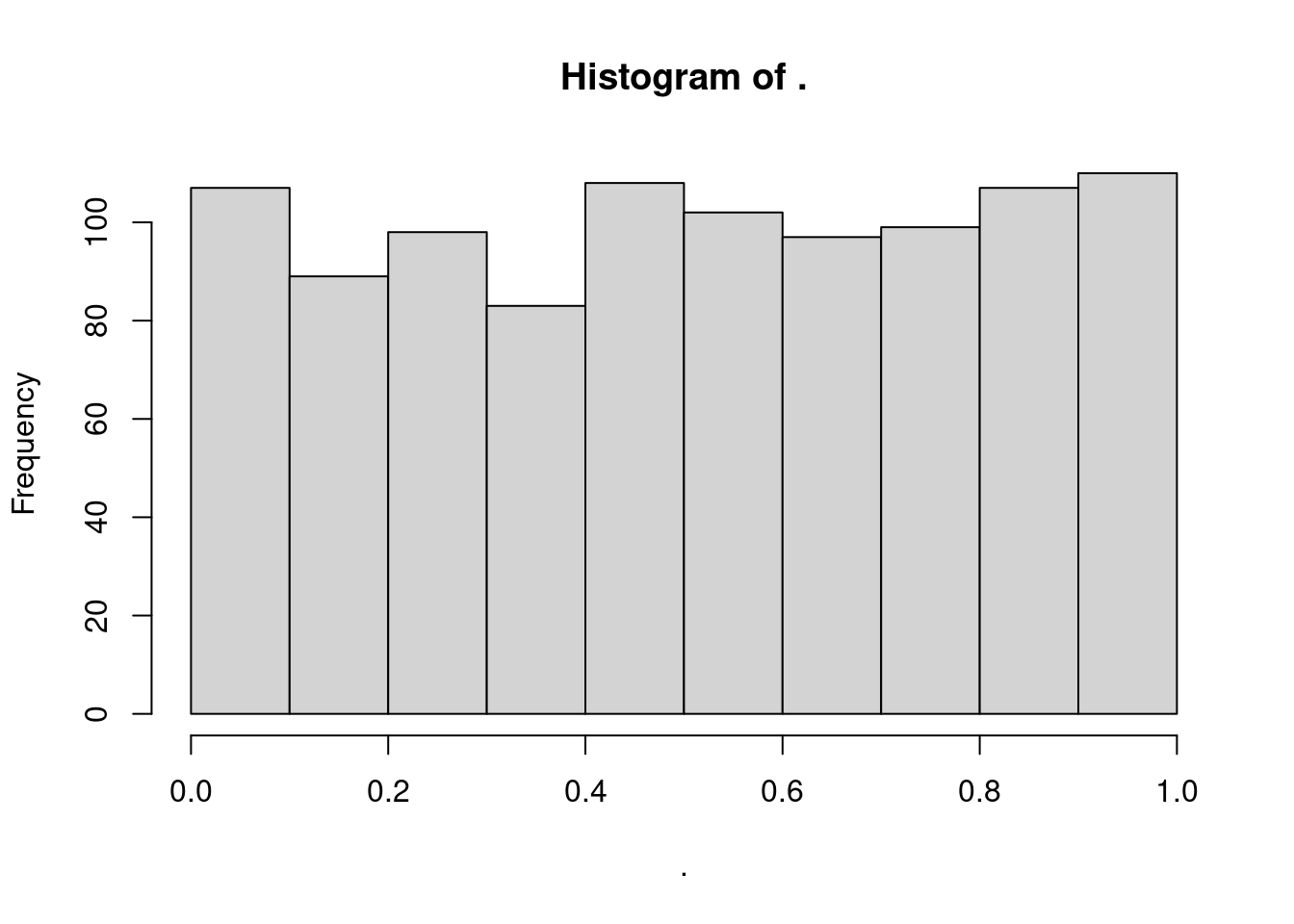
Wir sehen, dass die p-Werte im Intervall [0;1] gleichverteilt (uniformly distributed) sind.
Wissen Sie warum?
Definition des p-Werts
Zum Abschluss nochmal das Wichtigste wiederholt: die Defintion des p-Werts
Bei einem statistischen Test stellt man eine Nullhypothese auf (typischerweise die Hypothese, dass der vermutete Effekt nicht besteht) und errechnet aus der Stichprobe eine sog. Test-Statistik, die die Stärke des vermuteten Effekts quantifiziert. Dann berechnet man, wie wahrscheinlich es wäre, einen Effekt mit mindesens der ebobachteten Stärke (also eine Test-Stastistik mindestens so groß wie der beobachtete Wert) zu erhalten, wenn man annimmt, dass die Nullhypothese zutrifft (das also die Bebachtung keinen echten Effekt, sondern nu Zufallsfluktuation widerspiegelt). Diese Wahrscheinlichkeit nennt man den p-Wert.
Hausaufgabe
Erstellen Sie ein Säulendiagramm, das die Mittelwerte der Körpergrößen der erwachsenen NHANES-Probanden zeigt, aufgeschlüsselt nach Ethnie und Gescglecht. Natürlich haben wir das bereits in früheren Aufgaben gemacht. Ergänzen Sie das Diagramm aber diesmal, indem Sie an der Oberkante jeder Säule einen Fehlerbalken einzeichnen, der das 95%-Kofidenzintervall des jeweiligen Mittelwerts zeigt.
Erstellen Sie ein Quarto-Notebook, dass den Code enthält, den Plot, sowie eine kurze Beschreibung, was der Plot darstellt, erstellen Sie daraus eine Standalone-HTML-Datei und laden Sie diese auf Moodle hoch.