Mehr zur Normalverteilung

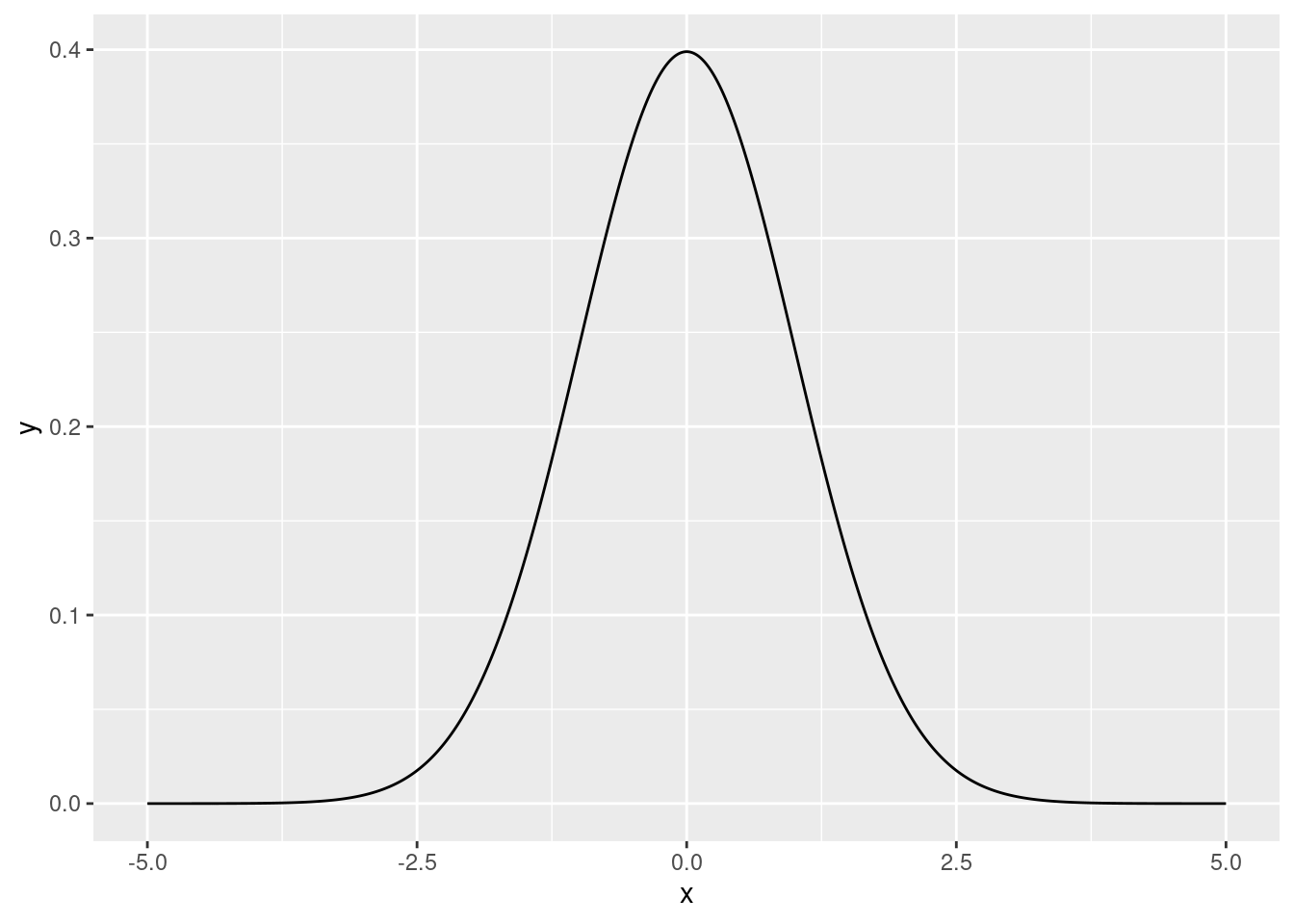
Vorlesung “Datananalyse in der Biologie”

Die Formel zur Standard-Normalverteilung

Die Funktion

\[ f_\mathcal{N}(x) = {\scriptsize \frac{1}{\sqrt{2\pi}}} e^{-x^2/2} \] nennt man die Wahrscheinlichkeits-Dichte-Funktion der Standard-Normalverteilung (probability density function of the standard normal distribution).

Sie sieht so aus:

suppressPackageStartupMessages( library(tidyverse) )

tibble( x = seq( -5, 5, length.out=1000 ) ) %>%
mutate( y = exp( -x^2/2 ) / sqrt(2*pi) ) %>%
ggplot + geom_line( aes( x=x, y=y ) )

Die R-Funktion dnorm ( für “density of the normal distribution”) berechnet diese Funktion:

x <- 0.7

c( 
  "mit Formel" =  exp( -x^2/2 ) / sqrt(2*pi),
  "mit dnorm"  =  dnorm( x ) )

mit Formel  mit dnorm 
 0.3122539  0.3122539 

Das wichtige an der Formel ist das \(e^{-x^2/2}\). Der Vorfaktor \(1/\sqrt{2\pi}\) dient lediglich der Normierung: er sorgt dafür dass das Integral (also die Fläche unter der Kurve) genau 1 ist. (Das liegt an dieser Formel, die man das Gauß-Integral nennt: \(\int_{-\infty}^\infty e^{-x^2}\text{d}x=\sqrt{\pi}\).)

Wir nennen den Graph einer Funktion eine Gaußsche Glockenkurve, wenn sie genau diese Form hat. Es ist aber immer noch eine Glockenkurve, wenn wir den Mittelwert verschieben, oder die Breite ändern. Für ersteres ersetzen wir \(x\) durch \(x-\mu\), um die Mitte zu einem gegebenen Wert \(\mu\) zu schieben, für letzteres teilen wir durch eine positive Zahl \(\sigma\), wobei \(\sigma>1\) die Glocke breiter werden lässt und \(0<\sigma<1\) schmaler.

Somit wird \(x\) zu \(\frac{x-\mu}{\sigma}\) und unsere Formel wird zu

\[f_\mathcal{N(\mu,\sigma)}(x) = {\scriptsize \frac{1}{\sqrt{2\pi\sigma^2}}} e^{\normalsize -\frac{(x-\mu)^2}{2\sigma^2}} \]

Auch diese Formel kann dnorm berechnen:

x <- 2.7
mu <- 3
sigma <- 2

c( 
  "mit Formel" =  exp( - (x-mu)^2 / (2*sigma^2) ) / sqrt(2*pi*sigma^2),
  "mit dnorm"  =  dnorm( x, mean=mu, sd=sigma ) )

mit Formel  mit dnorm 
 0.1972397  0.1972397 

Hier der Graph für \(\mu=3\) und \(\sigma=2\):

suppressPackageStartupMessages( library(tidyverse) )

tibble( x = seq( -3, 11, length.out=1000 ) ) %>%
mutate( y = dnorm( x, mean=3, sd=2) ) %>%
ggplot + geom_line( aes( x=x, y=y ) )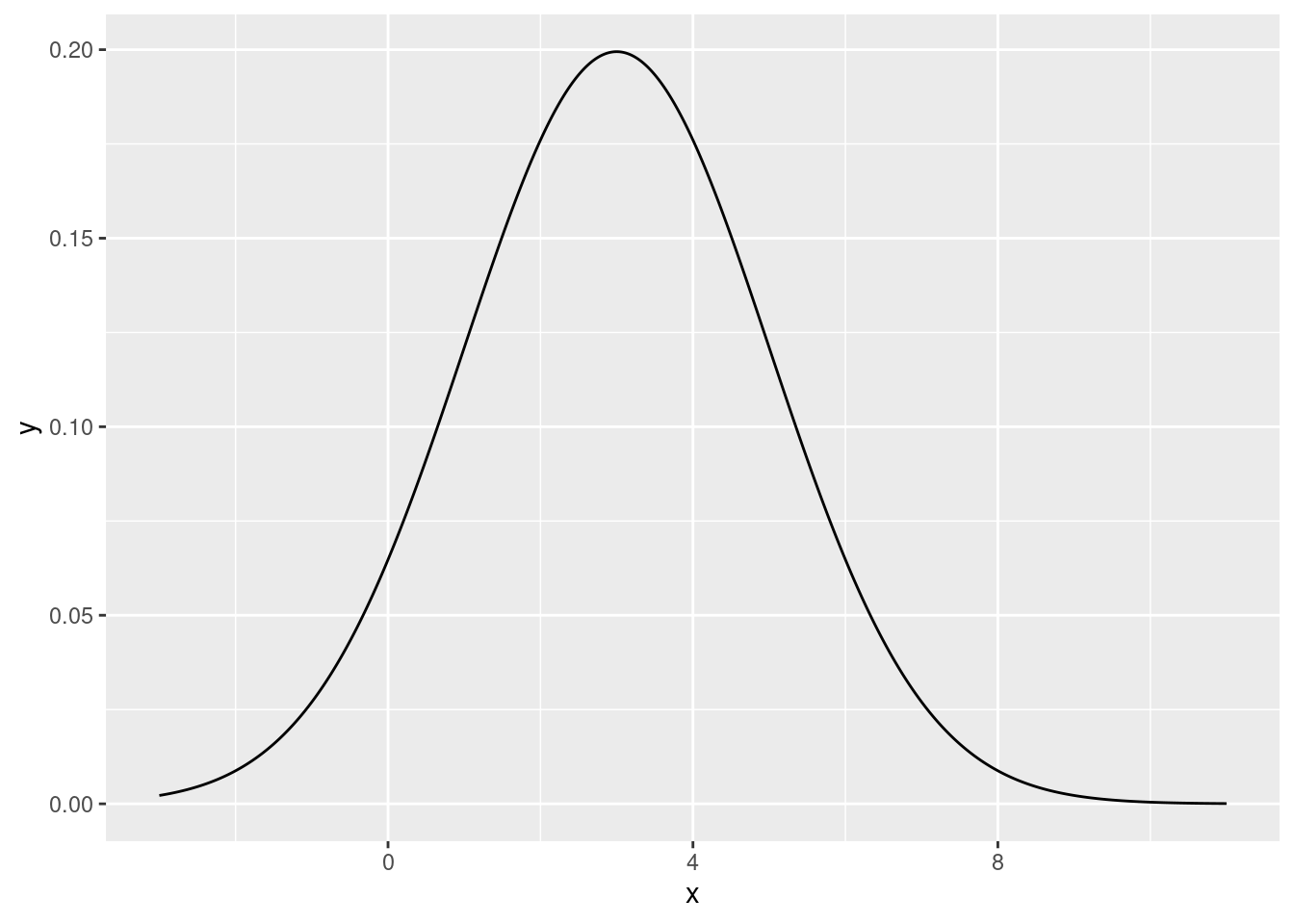

Wenn man dnorm keine Argumente für mean und sd übergibt, wreden die Standards \(\mu=0\) und \(\sigma=1\) (die Standard-Normal-Verteilung) verwendet.

Normalverteilte Zufallswerte

Die Funktionrnorm (random normally distributed data) erzeugt Daten, die normal verteilt sind:

rnorm( 1000, mean=3, sd=2 ) -> random_values

str(random_values)

 num [1:1000] 1.121 4.751 0.584 0.149 3.053 ...

Wir vergleichen das Histogramm dieser Werte mit der Dichtefunktion:

tibble( x = seq( -3, 11, length.out=10000 ) ) %>%
mutate( y = dnorm( x, mean=3, sd=2 ) ) -> density_table

ggplot(NULL) + 
  geom_histogram( aes( x=x,y=after_stat(density) ), data = tibble( x=random_values ), bins=50 ) +
  geom_line( aes( x=x, y=y ), data = density_table, col="magenta" ) +
  geom_vline( xintercept = c( 3, 4 ), col="magenta", lty="dashed" )

Anmerkungen zum Code:

• Die beiden geom-Layers haben verschiedene Daten-Tabellen. Daher bekommt ggplot gar keine Tabelle (NULL) und die beiden geoms bekommen jeweils ihre eigene Tabelle mit data=.
• Eine Dichtefunktion ist immer so skaliert, dass die Fläche 1 ist. Damit wir das Histogramm damit vergleichen können, müssen wir auch die Höhe der Histogramm-Säulen mit einem Faktor multiplizieren, der so gewählt ist, dass danach alle Säulen zusammen auch die Fläche 1 haben. Dafür sorgt das y=after_stats(density).

Nun sehen wir auch, wie man eine Dichtefunktion “liest”:

Dazu berechnen wir, wie groß die Wahrscheinlicheit ist, dass ein Wert, den man aus unserer Normalverteilung (mit \(\mu=3\) und \(\sigma=2\)) zwischen 3 und 4 liegt. Das ist genau die Fläche, die durch die magentafarbenen Kurve, die beiden gestrichelten vertikalen Linien, und die x-Achse begrenzt wird. Um die Fläche zu ermitteln, verwenden wir pnorm. Es bestimmt die Fläche links von eine gegebenen vertikalen Linie bei x. Wir setzten einmal x auf 3 und einmal auf 4 und berechnen die Differenz:

pnorm( 4, mean=3, sd=2 ) - pnorm( 3, mean=3, sd=2 )

[1] 0.1914625

Wenn dies tatsächlich die Wahrscheinlichkeii ist, dass eine zufällig gezogene Zahl zwischen 3 und 4 liegt, sollte der Anteil unserer Zufallswerte, die in diesem Bereich liegen, in etwa 19% sein. Wir prüfen das:

mean( random_values > 3 & random_values < 4 )

[1] 0.188

(Hier haben wir & verwendet, was die logische “und”-Operation bezeichnet.)

Die Funktion pnorm bezeichnet man als die kumulative Verteilungsfunktion (cumulative distribution function, cdf) der Normalverteilung. pnorm(x) ist das Integral von dnorm(x) von \(-\infty\) bis x.

Parameter der Normalverteilung

Wie erwähnt hat die Normalverteilung zwei Parameter: \(\mu\) und \(\sigma\). Diese stellen Mittelwert und Standardabweichung dar. Wir ziehen also nochmal Zufallszahlen aus einer Normalverteilung mit \(\mu=3\) und \(\sigma=2\) und bestimmen Mittelwert und Standardabweichung der Stichprobe:

rnorm( 1000, mean=3, sd=2 ) -> random_values

mean( random_values )

[1] 2.972445

sd( random_values )

[1] 2.160888

Zentraler Grenzwertsatz

Der Zentrale Grenzwertsatz (central limit theorem) besagt:

Wenn man eine große Anzahl voneinander unabhängiger Zufallsgrößen aufsummiert, so ist die Summe näherungsweise normalverteilt. Je mehr Werte man aufaddiert, desto näher kommt man der exakten Normalverteilung.

Der Satz gilt nur unter gewissen Voraussetzungen, insbesondere, dass die einzelnen Zufallsgrößen endliche Varianz haben, aber das ist fast immer der fall, daher ignorieren wir es.

Demonstration

Hier ist ein Histogramm von 10000 Werten, die aus einer uniformen Verteilung gezogen wurden:

hist( runif( 10000 ) )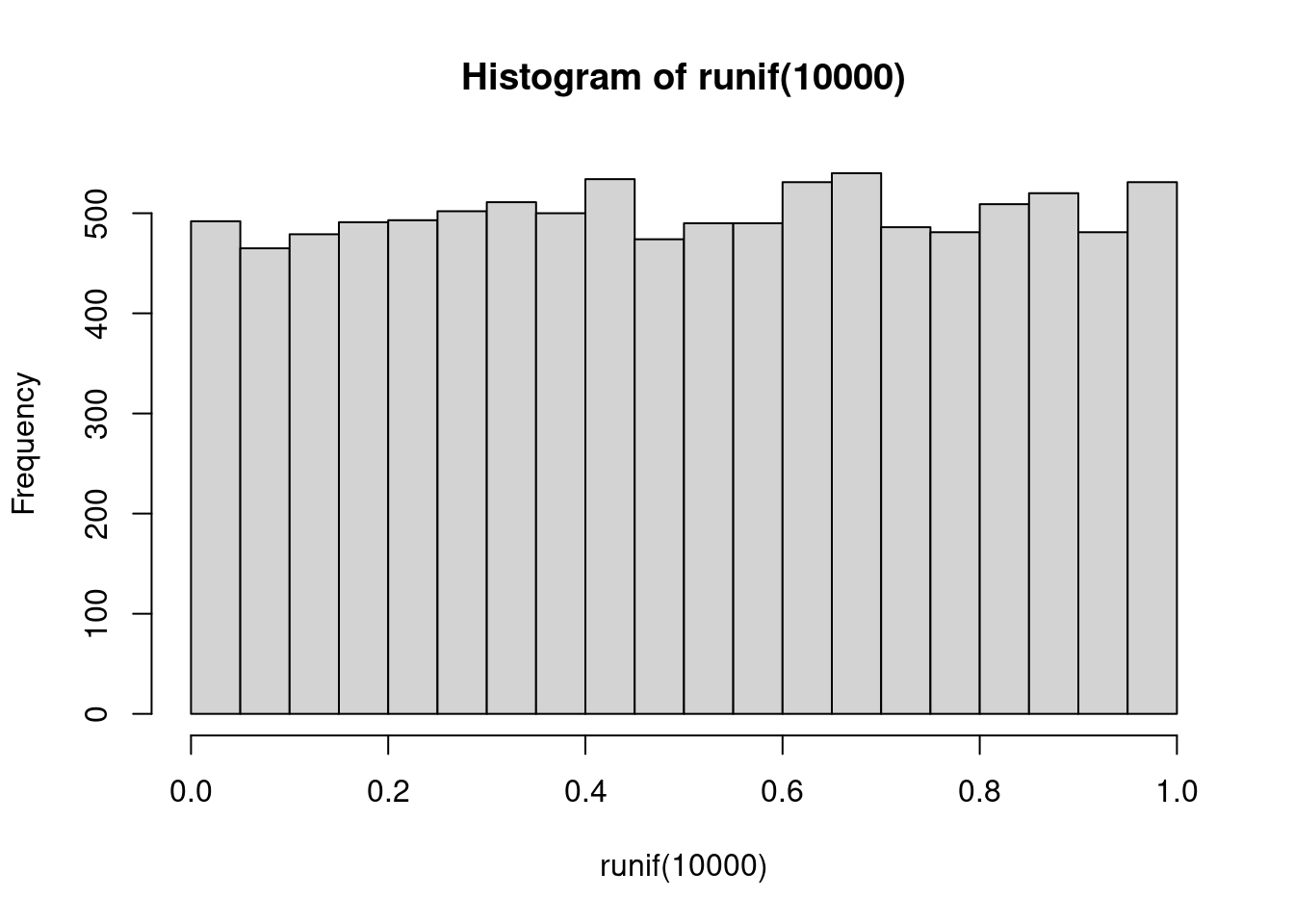

(Ignorieren Sie in diesem Abschnitt den R-Code; das ist “altes” R, kein Tidyverse.)

Hier sind 10000 Werte, die jeweils die Summe zweier uniform verteilter Zufallszahlen sind:

hist( runif(10000) + runif(10000) )

Wenn wir jeweils drei Werte aufaddieren, beginnt man die Glockenform zu erkennen:

hist( runif(10000) + runif(10000) + runif(10000) )

Nun jeweils 5 Werte, und dazu die Dichte einer Normalverteilung mit Mittelwert \(5\cdot\frac{1}{2}\) und Varianz \(5\cdot\frac{1}{12}\). (Das sind 5-mal der Mittelwert und die Varianz der Standard-uniformen Verteilung.)

hist( 
  runif(10000) + runif(10000) + runif(10000) + runif(10000) + runif(10000), 
  breaks=30, freq=FALSE )
lines( 
  seq(0,5,l=1000), 
  dnorm( seq(0,5,l=1000), mean=2.5, sd=sqrt(5/12) ), col="magenta" )

Die 68-95-99.7-Regel

Wie wahrscheinlich ist es, dass ein Wert, der aus einer Standard-Normalverteilung gezogen wurde, zwischen -1 und 1 liegt?

pnorm(1) - pnorm(-1)

[1] 0.6826895

Und wie wahrscheinlich ist es, dass ein Wert, der aus einer Normalverteilung mit Mittelwert 10 und Standardabweichung 3 zwischen 7 und 13 liegt, also höchstens wine Standardabweichung vom Mittewleert abweicht?

pnorm( 13, mean=10, sd=3 ) - pnorm( 7, mean=10, sd=3 )

[1] 0.6826895

Natürlich derselbe Wert!

Wie wahrscheinlich ist es, dass man höchstens zwei Standardabweichungen vom Mittelwert abweicht?

pnorm(2) - pnorm(-2)

[1] 0.9544997

Und für 3 Standardabweichungen?

pnorm(3) - pnorm(-3)

[1] 0.9973002

Wie fassen zusammen:

Die Wahrscheinlichkeit, dass eine normalverteilte Zufallsvariable höchstens um \(\left\{\begin{array}{c}1\\2\\3\end{array}\right\}\) Standardabweichung(en) vom Mittelwert abweicht, beträgt \(\left\{\begin{array}{c}68,\!3\%\\95,\!4\%\\99,\!7\%\end{array}\right\}\).

Diese drei Zahlen – 68% / 95% / 99.7% – sollte man auswenig kennen!

Man kann sich auch merken:

• Das eine normalverteilte Zufallsgröße mehr als eine Standardabweichung vom Mittelwert abweicht, kommt in 1 von 3 Fällen, also ziemlich oft, vor.
• Eine Abweichung von mehr als zwei Standardabweichung kommt in 1 von 20 Fällen, also durchaus manchmal, vor.
• Eine Abweichung von mehr als zwei Standardabweichung kommt in 1 von 370 Fällen, also eher selten, vor.

Dies sollten Sie stets beachten, wenn Sie einen Standardfehler bewerten.

Echte Daten

Wir laden nochmal die NHANES-Daten und sehen uns die Körpergrößen der Männer an:

read_csv( "Downloads/nhanes.csv", show_col_types=FALSE ) -> nhanes

nhanes %>%
filter( gender == "male", age >=18, !is.na(height) ) %>%
pull( height ) -> men_heights

hist( men_heights )

Wir bestimmen Mittelwert und Standardabweichung

men_heights_mean = mean( men_heights )
men_heights_sd = sd( men_heights )

men_heights_mean

[1] 173.4809

men_heights_sd

[1] 7.676302

Welcher Anteil der Männer ist wohl mehr als 2 Standardabweichungen größer als der Durchschnitt, also größer als

men_heights_mean + 2*men_heights_sd

[1] 188.8335

Nach der 68-95-99,7-Regel sollten 95% der Männer innerhalb von 2 Standardabweichungen liegen, und somit je 2,5% drüber und 2,5% drunter.

mean( men_heights > men_heights_mean + 2*men_heights_sd )

[1] 0.02471483

Das kommt gut hin.

Wir sehen: Da die Daten näherungsweise normalverteilt sind, können wir Berechnungen anstellen, selbst wenn wir die Daten selbst nicht haben, sondern nur die zwei Parameter Mittelwert und Standardabweichung.

Beispiel: Wie viele Männer sind größer als 2 m?

Dazu fargen wir: Wie viele Standardabweichungen liegt 200 cm über dem Mittel?

z <- ( 200 - men_heights_mean ) / men_heights_sd
z

[1] 3.454674

200cm liegt \(z=3.5\)mal über dem Mittelwert. So einen Wert, der die Abweichung vonm Mittelwert in Relation zur Standardabweichung setzt, nennt man einen z-Wert: \(z=(x-\mu)/\sigma\)

Was ist die Wahrscheinlichkeit, so weit drüber zu liegen? pnrom gibt uns die Wahrscheinlichkeit, dass \(z\) unter dem gegebenen Wert leigt, also müssen wir das Komplement (“eins minus”) berechnen:

1 - pnorm( z )

[1] 0.0002754788

Alternativ kann man auch rechnen:

1 - pnorm( 200, mean=men_heights_mean, sd=men_heights_sd )

[1] 0.0002754788

Das ist nur 1 Mann unter 3630. Haben wir so einen in unserer Stichprobe?

sum( men_heights > 200 )

[1] 0

Aufgabe

In Deutschland ist der Mittelwert der Körpergröße erwachsener Männer 178 cm mit einem Mittelwert von 7 cm. Wie viele Männer über 2 Meter gibt es wohl unter den insgesamt 33 Millionen erwachsenen Männern, die in Deutschland leben?

Aufgabe

Ein Düngemittel erhöht die Größe von Zwiebeln um 10%. Aus vorherigen Untersuchungen wissen Sie, dass das Gewicht von Zwiebeln der Sorte X normalverteilt ist mit einem Erwartungswert von 80 g und einer Standardabweichung von 9 g. Sie sähen Zwiebeln auf zwei gleichartigen Feldern aus und verwenden auf einem der beiden Felder den Dünger.

Nehmen wir an, dass der Dünger das Gewicht im Mittel tatsächlich um 10% erhöht, dass also das Gewicht gedüngter Zwiebeln normalverteilt ist mit Erwartungswert 88g statt 80g, und derselben Standardabweichung, 9g.

Schreiben Sie Code, der folgendes simuliert: - 10 Zwiebel werden vom ungedüngten Feld geerntet, gewogen, und der Mittelwert wird ermittelt. - Ebenso werden 10 Zwiebeln vom gedüngten feld geerntet, auch gewogen und gemittelt. - Die Differenz der beiden Mittelwerte wird ermittelt.

Anleitung: - Ziehen Sie 10 Zufallszahlen aus einer Normalverteilung mit Erwartungswert 80g und Standardabweichung 8g, und bestimmen Sie den Mittelwert der 10 Zahlen. - Dann machen Sie dasselbe nochmal, aber mit Erwartungswert 88g. - Ziehen Sie den ersten Mittelwert vom zweiten ab.

Lassen Sie diese Simulation nun (mit replicate) 3000-mal laufen und plotten Sie das Histogramm der Differenzen.

Wie wahrscheinlich ist es, dass die gedüngten Zwiebeln schlechter abschneiden als die ungedüngten?

Mittelwerte

Mittelwerte berechnet man, indem man viele Einzelwerte aufaddiert (und dann durch die Anzahl teilt). Somit kann man den zentralen Grenzwertsatz anwenden und folgern: Mittelwerte sind (näherungsweise) normalverteilt.

Das gilt selbst dann, wenn die Einzelwerte nicht normalverteilt sind.

Grundgesamtheit und Stichprobe

Wir verwenden nun das Beispiel “Körpergröße der erwachsenen Männer in Deutschland”, um etwas Terminologie einzuführen.

• Wir haben hier eine Grundgesamtheit (population), nämlich alle erwachsenen Männer in Deutschland.

• Jedem Mann ist eine Zahl zugeordnet, die Körpergröße in cm.

• Die Verteilung (distribution) der Körpergröße ist die Angabe, wie wahrscheinlich jede Wert bzw. jedes Interval ist, bzw. wie häufig es in der Grundgesamtheit ist.

• Wir können die Verteilung durch eine Dichtefunktion (d.h. ein Histogramm mit unendlich feinen Bins) darstellen. Wenn wir die Form der Dichtefunktion kennen, genügt es, die Art (“Familie”) der Verteilung (z.B., Normalverteilung) anzugeben, und die zugehörigen Parameter (bei Normalverteilung: Erwartungswert und Standardabweichung).

• Jeden einzelnen Mann der gesamten Bevölkerung zu vermessen ist ein viel zu großer Aufwand. Daher “ziehen” wir eine Stichprobe (draw a sample) mit einer überschaubaren Anzahl \(n\) an Personen aus. Wir nennen \(n\) die Länge oder den Umfang der Stichprobe (sample size).

• Dabei wählen wir jeden einzelnen Probanden zufällig und unabhängig von den anderen aus der Grund-Gesamtheit aus. (SO ein Vorgehen ist nicht )

• Wir fragen uns, wie nah Mittelwert und Standardabweichung der Stichprobe an den Mittelwert und Standardabweichung der Gesamt-Bevölkerung liegt.

• Der Mittelwert unserer Stichprobe ist eine Zufallsvariable – denn er hängt von unserer zufälligen Auswahl an Probanden ab.

• Somit hat er eine Wahrscheinlichkeitsverteilung, aber da wir nur eine Stichprobe, und somit nur einen Wert haben, können wir diese sog. Stichproben-Verteilung (sampling distribution) nicht direkt ermitteln.

• Wir können aber allgemeine Aussagen darüber machen, welche Stichprobenverteilung sich ergibt aus einer gegebenen Grundgesamtheits-Verteilung und einer gegebenen Methode, die Stichprobe zu ziehen.

[Einschub zum Word “sample”: In der Statistik bezeichnet man alle untersuchten Probanden zusammen als eine Stichprobe (a sample, singular). “Stichprobe” oder “Probe” bezeichnet also hier einen kleinen Teil (die \(n\) Probanden), der stellvertretend für das Ganze (die Gesamt-Bevölkerung) steht. Ebenso ist z.B. eine Blutprobe (blood sample) eine kleine Menge Blut, die stellvertretend für das gesamt Blut eines Patienten untersucht wird. Das kann verwirrend sein: Statistiker sagen: “We have blood values from a sample of 10 patients.” (singular) – Mediziner/Biologen sagen: “We have samples from 10 patients.” (plural)]

Stichproben-Mittelwerte

Nehmen wir an, in der Grundgesamtheit aller erwachsenen Männerin Deutschland sei die Körpergröße normalverteilt mit Mittelwert 178 cm und Standardabweichung 7 cm.

Wir wissen das aber nicht und möchten es heraus finden, indem wir \(n=1000\) Männer vermessen. Wie genau kommen wir an den wahren Mittelwert heran?

Wir simulieren die Erhebung einer Stichprobe von 1000 Probanden

heights <- rnorm( 1000, mean=178, sd=7 )

Wir bestimmen den Mittelwert

mean( heights )

[1] 177.6779

Um die sampling distribution des Stichproben-Mittelwerts zu ermitteln, können wir simulieren, dass wir 3000 mal eine Stichprobe zu je 1000 Männern ziehen:

many_means <- replicate( 3000, mean( rnorm( 1000, mean=178, sd=7 ) ) )

Hier ist das Histogramm der vielen Mittelwerte:

hist( many_means )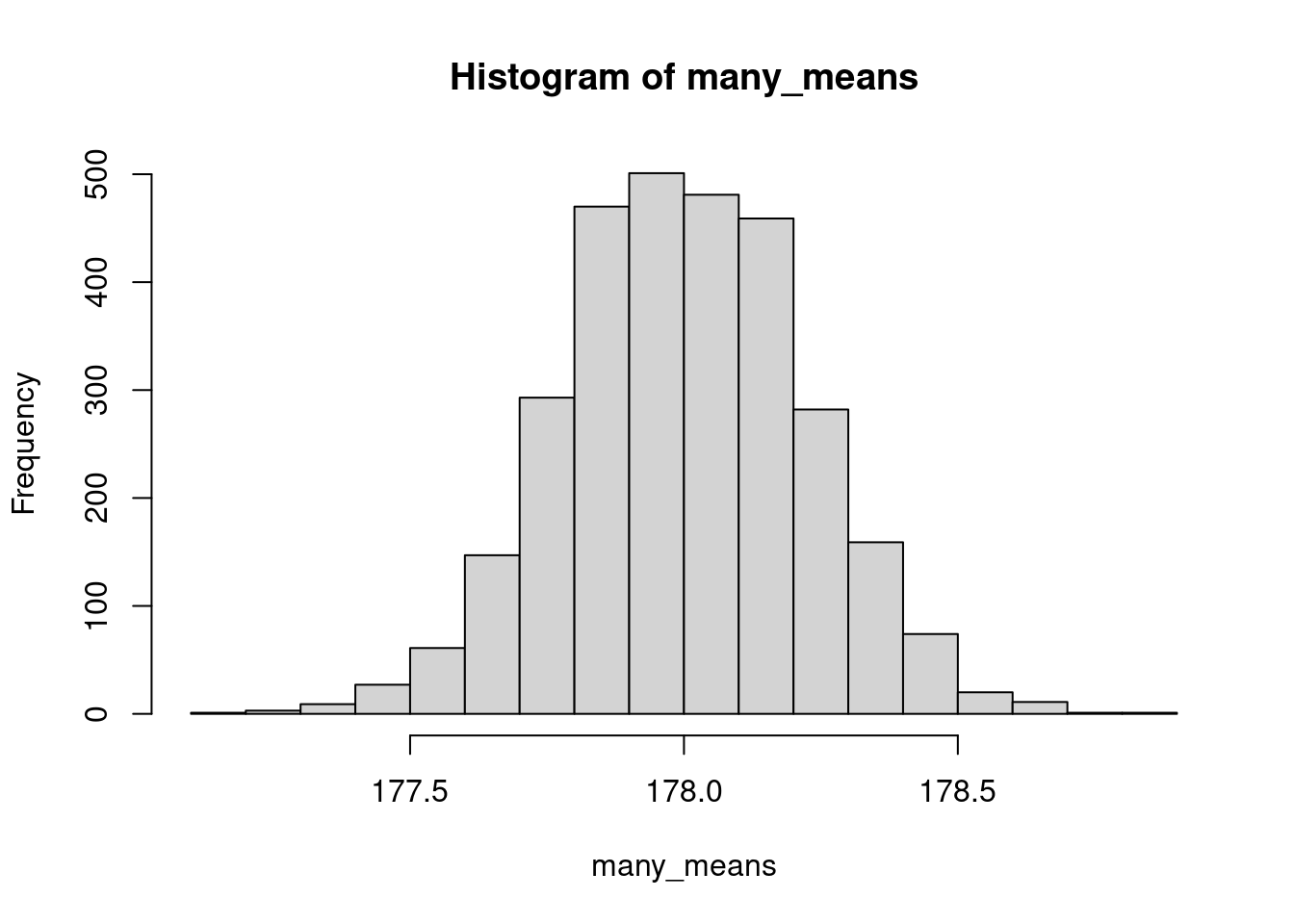

Wie zu erwarten war, erkennen wir:

• Die Mittelwerte sind normalverteilt
• Der Mittelwert der Mittelwerte liegt bei 178 cm.
• Die Standardabweichung ist

sd( many_means )

[1] 0.2229138

Diesen Wert haben wir durch Simulation ermittelt; wir hätten ihn aber auch ausrechnen können: die Standardabweichung der Stichproben-Mittelwerte (der Standardfehler des Mittelwerts) is die Standardabweichung der Einzelwerte in der Grundgesamtheit (also 7cm), geteilt durch die Quadratwurzel des Stichproben-Umfangs (also 1000 Männer):

7 / sqrt(1000)

[1] 0.2213594

Unser “Computer_Experiment” hat also die Formel zum Standardfehler des Mittelwerts bestätigt.

Stichproben-Standardabweichung

In der Rechnung eben haben wir die Standardabweichung der Grundgesamtheit (7 cm) verwendet. Die wissen wir aber nicht. Wir müssen die Standardabweichung der Stichprobe nehmen.

Wie genau liegt diese denn am wahren Wert? Wir erstellen wieder eine sampling distribution:

many_sd <- replicate( 3000, sd( rnorm( 1000, mean=178, sd=7 ) ) )

hist( many_sd )

Unsere Schätzung des SEM wird also nicht sonderlich dadurch verfälscht, dass wir die Standardabweichung auch schätzen müssen.

Das ist aber sehr anders, wenn der Stichproben-Umfang klein ist! Hier dasselbe mit nur 10 Probanden:

many_sd <- replicate( 3000, sd( rnorm( 20, mean=178, sd=7 ) ) )

hist( many_sd )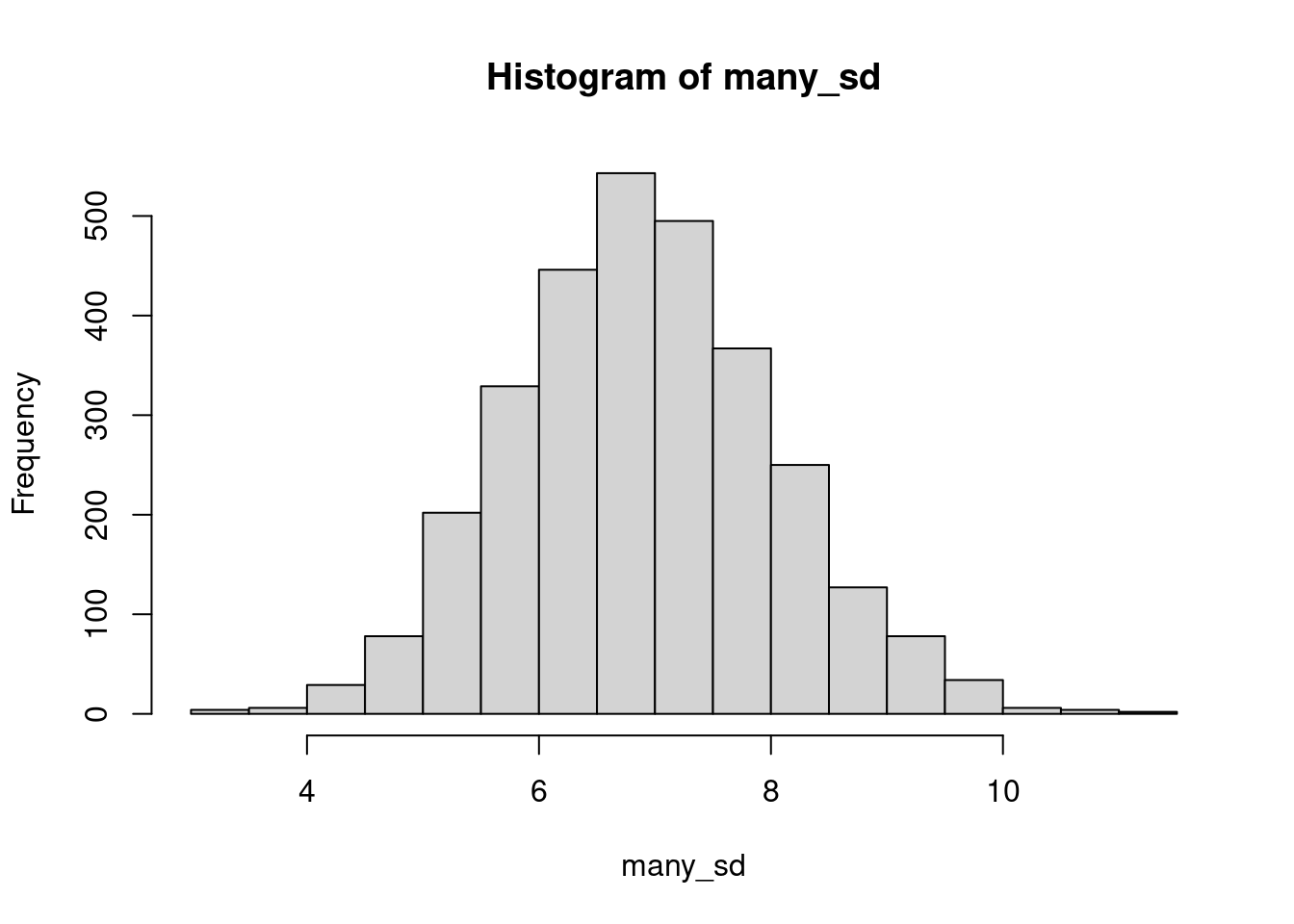

Mit dem wahren SD-Wert von 7 kommen wir auf einen Standardfehler des Mittelwerts von \(7/\sqrt{10}=2.2\).

Wenn wir aber z.B. eine SD-Schätzung von nur 4 erhalten hätten, würden wir für unserem Mittelwert einen Standardfehler von nur \(4/sqrt{10}=1.3\) ausweisen, also fälschlich behaupten, dass unser Stichproben-Mittelwert viel genauer ist als er es wirklich ist.

Daher darf die einfache Formel \(\text{SEM}=\text{SD}/\sqrt{n}\) nur verwendet werden, wenn man eine große Stichprobe (Faustregel \(n\gtrsim 50\) ) hat.

Bei kleinen Stichproben muss man ein Verfahren verwenden, dass die sog. Studentsche t-Verteilung verwendet.