m <- matrix( c( 63, 100-63, 45, 100-45 ), ncol=2 )
rownames(m) <- c( "improvement", "no improvement" )
colnames(m) <- c( "drug", "placebo" )
m drug placebo
improvement 63 45
no improvement 37 55Vergleich binomialer Anteile mit dem Fisher-Test
Vorlesung “Datenanalyse in der Biologie”
Beispiel: klinische Studie
Durch eine klinische Studie soll ein neuer Wirkstoff erprobt werden zur Behandlung einer Hautkrankheit (z.B. Psoriasis/Schuppenflechte). 200 Patienten mit dieser Krankheit werden in die Studie aufgenommen. Das Studienprotokoll ist wie folgt:
- Bei jedem der Patienten wird das Ausmaß der Hautausschläge oder Exzema vermessen und fotografisch dokumentiert.
- Jeder Patient enthält Tabletten, die für einen Monat täglich einzunehmen sind.
- Bei 100 der Patienten enthalten die Tabletten den neuen Wirkstoff, bei den anderen 100 enthalten sie keinen Wirkstoff (Plazebo).
- Nach Ablauf des Monats wird das Ausmaß der Ausschläge wieder dokumentiert und vermessen. Ein Dermatologe beurteilt durch vorher/nachher-Vergleich, ob sich das Krankheitsbild (a) verbessert hat oder (b) gleich geblieben oder schlechter geworden ist.
- Die Studie ist doppelt verblindet (double-blind study), d.h. weder die Patienten, noch die Ärzte, die mit den Patienten sprechen oder die Vergleiche durchführen, wissen, wer Wirkstoff und wer Plazebo erhalten hat. Erst nach Abschluss der Vergleiche wird aufgelöst, wer was bekommen hat.
Das Ergebnis ist: Eine Verbesserung wurde festgestellt bei 40 der 100 Patienten, die Plazebo erhalten haben, und bei 63 der Probanden, die den Wrkstoff erhalten haben.
Vier-Felder-Tafel
Wir stellen diese Zahlen zunächst in einer sog. Vier-Felder-Tafel (contingency table) oder Kreuztabelle (cross tabulation) dar:
Das es auch ohne Wirkstoff oft zu Verbesserung kommt ist nicht verwunderlich, wenn wir annehmen, dass es sich um eine chronische Krankheit handelt, die in Schüben kommt, die kommen und gehen. Wir müssen usn daher fragen, ob wir vielleicht zufällig in underer Plazebo-Gruppe mehr Patienten hatten, deren Schub gerade ohnehin am Ablingen war, oder ob der Unterschied wirklich auf den Wirkstoff zurück zu führen ist.
Relatives Risiko und Odds Ratio
Man fasst Zwei-Felder-Tafeln gerne auf zwei Weisen zusammen:
Relatives Risiko: Das Risiko, keine Verbesserung zu erfahren, können wir aus den Daten für die Plazebo-Gruppe auf 55/100=0.55 schätzen und für die Wirkstoff-Gruppe auf 37/100=0.37. Das Risiko verringert sich also um den Faktor 0.37/0.55=.67. Diesen Wert nenntn man eine Schätzung des relativen Risikos (relative risk, RR).
Quotenverhältnis: Die Quote (engl. “the odds”, ein Plural-Wort) für eine Verbesserung beträgt in der Wirkstoff-Gruppe 63:37 = 1.70:1 und in der Plazebo-Gruppe 45:55 = 0.82:1. Das Verhältnis dieser beiden Quoten (Quotenverhältnis, engl. “odds ratio”) ist also
(63/37) / (45/55)[1] 2.081081Während das relative Risiko anschaulicher ist, wird für Rechnungen oft das Quotenverhältnis bevorzugt, da es symmetrisch ist: Um vom Quotenverhältnis für eine Verbesserung zum Quotenverhältnis für eine Nicht-Verbesserung zu kommen, braucht man nur den Kehrwert zu bilden.
Das Quotenverhältnis hat auch die Eigenschaft, dass man auf den selben Wert kommt, egal ob man in der Vier-Felder-Tafel (s.o.) die Spaltenverhältnisse durcheinander teilt – (63:37) : (45:55) – oder die Zeilenverhältnisse – (63:45) : (37:55):
(63/45) / (37/55)[1] 2.081081(Erinnern sich dazu an ihre Schulzeit, Stichwort “Doppelbruch”.)
Nullhypothese und Hypothesentest
Um nun einen Hypothesentest durchzuführen und einen p-Wert zu erhalten, brauchen wir eine Nullhypothese, die unsere Erwartung beschreibt für die Annahme, dass der Wirkstoff keine Wirkung hat. Natürlich lautet diese Nullhypothese: “Es gibt keinen Unterschied zwischen Wirkstoff und Plazebo”.
Diese Nullhypothese machen wir nun quantitativ, indem wir sagen: Jeder Patient ist ein Bernoulli-Experiment, d.h. ein Zufallsexperiment mit zwei möglichen Ergebnissen, nämlich Erfolg (Verbesserung) oder Fehlschlag (keine Verbesserung). Die Nullhypothese ist also, dass die Erfolgswahrscheinlichkeit in beiden Gruppen dieselbe ist
Warum der Binomialtest nicht evwrendet werden kann
Eine erste Idee könnte sein, die Erfolgswahrscheinlichkeit unter der Nullhypothese (Wirkstoff = Plazebo) auf den Wert aus der Plazebo-Gruppe zu setzen, also 45/100 = 0.45, und einen Binomialtest für die Wirkstoff-Gruppe durchzufüḣren:
binom.test( 63, 100, 0.45 ) # FALSCH!
Exact binomial test
data: 63 and 100
number of successes = 63, number of trials = 100, p-value = 0.0003838
alternative hypothesis: true probability of success is not equal to 0.45
95 percent confidence interval:
0.5276484 0.7244334
sample estimates:
probability of success
0.63 Aber: Hier behandeln wir den Wert 45/100 also ob der genaue Wert a priori exakt bekannt ist. Es ist aber ein aus Zufallsdaten geschätzter Wert, ganz genauso wir der Wert 63/100.
Fisher-Test
R. A. Fisher schlug daher einen Test vor, der alle vier Einzelwerte der Vier-Felder-Tafel in Betracht zieht. Wir übergeben der fisher.test-Funktion unsere Vielr-Felder-Tafel:
m drug placebo
improvement 63 45
no improvement 37 55fisher.test( m )
Fisher's Exact Test for Count Data
data: m
p-value = 0.01565
alternative hypothesis: true odds ratio is not equal to 1
95 percent confidence interval:
1.137985 3.813096
sample estimates:
odds ratio
2.07331 Nun erhalten wir einen gültigen p-Wert, nämlich 1.57%.
Der Fisher-Test betrachtet das Quotenverhältnis (odds ratio): Mit “Quote” (odds) meinen wir das Verhältnis der Anzahl Patienten mit verbessung zur Anzahl Patienten ohne Verbesserung, also 63:37 für die Wirkstoffgruppe und 45:55 für die Plazebo-Gruppe. Die Nullhypothese lautet dass die wahren Werte dieser Quoten für beide Gruppen gleich ist, dass das wahre Verhältnis der beiden Quoten also 1:1 ist (das heisst nicht, dass die einzelnen Quoten 1:1 wären, nur, dass sie gleich sind).
Nun abstrahieren wir die Situation der Nullhypothese durch ein Urnenmodell (urn modell): Eine Urne (d.h. ein undurchsichtiger Beutel) enthalte 200 Kugeln (balls) für die 200 Patienten. 108 der Kugeln sind rot und 92 Kugeln sind weiß. Die roten Kugeln stehen für die Erfolge (Patienten mit Verbesserung), die weißen für die Fehlschläge (keine Verbesserung).
Nun stellen wir die randomisierte Zuordnung der Probanden zu Wirkstoff und Plazebo dar, indem wir blind (also zufällig) 100 Kugeln aus der Urne ziehen, die für die Patienten stehen, die Wirkstoff erhalten haben. Die verbleibenden 100 Kugeln stehen für die Patienten, die Plazebo erhalten haben. Wir erstellen daraus eine Vier-Felder-Tafel.
Zur Verdeutlichung hier nochmal unsere ursprüngliche Vier-Felder-Tafel,
m drug placebo
improvement 63 45
no improvement 37 55nun mit abgeänderter Beschriftung:
m2 <- m
colnames( m2 ) <- c( "aus Urne gezogen", "in Urne verblieben" )
rownames( m2 ) <- c( "rot (Erfolg)", "weiß (kein Erfolg)" )
m2 aus Urne gezogen in Urne verblieben
rot (Erfolg) 63 45
weiß (kein Erfolg) 37 55Wenn unsere Nullhypthese zutrifft, wenn der Wirkstoff also wirklich nicht besser als Plazebo wirkt, dann sollte die Wahrscheinlichkeit, so eine Vier-Felder-Tafel bei unserem Urnen-Modell zu erhalten, oder eine noch extremer von der Erwartung abweichende Tafel zu bekommen, nicht zu klein sein.
Simulation
Zur Übung schreiben wir eine Simulation.
(Den exakten R-Code hier brauchen Sie sich nicht merken; Sie sollten aber das Prinzip verstehen.)
Zunáchst hier nochmal die Vier-Felder-Tafel, nun mit Randsummen (marginals):
addmargins( m2 ) aus Urne gezogen in Urne verblieben Sum
rot (Erfolg) 63 45 108
weiß (kein Erfolg) 37 55 92
Sum 100 100 200Wir simulieren eine Urne mit 108 roten und 92 weißen Kugeln:
urn <- c( rep( "red", 108 ), rep( "white", 92 ) )Wir durchmischen diesen Vektor (mit der Funktion sample, die zufällige Permutationen auswürfelt)
set.seed( 13245768)
urn <- sample( urn )
urn [1] "red" "red" "red" "white" "white" "white" "red" "white" "red"
[10] "red" "red" "white" "red" "red" "red" "red" "red" "red"
[19] "red" "red" "red" "red" "red" "white" "white" "red" "white"
[28] "white" "red" "red" "red" "white" "white" "white" "red" "white"
[37] "white" "red" "white" "red" "white" "red" "red" "white" "white"
[46] "red" "white" "red" "white" "red" "white" "white" "red" "white"
[55] "white" "white" "white" "red" "red" "white" "white" "red" "red"
[64] "white" "red" "white" "white" "white" "red" "red" "red" "white"
[73] "red" "red" "white" "white" "red" "white" "white" "white" "red"
[82] "white" "red" "white" "white" "red" "white" "red" "white" "white"
[91] "white" "red" "red" "white" "red" "white" "red" "red" "red"
[100] "red" "white" "white" "red" "red" "red" "red" "white" "red"
[109] "white" "white" "white" "white" "red" "red" "red" "white" "white"
[118] "white" "white" "red" "red" "red" "red" "red" "red" "red"
[127] "red" "red" "white" "white" "red" "white" "white" "red" "white"
[136] "red" "white" "red" "white" "white" "red" "white" "white" "white"
[145] "red" "red" "white" "white" "red" "white" "white" "white" "white"
[154] "white" "white" "red" "red" "white" "white" "red" "red" "red"
[163] "white" "red" "red" "red" "white" "red" "white" "white" "white"
[172] "red" "red" "red" "white" "red" "white" "red" "red" "red"
[181] "red" "red" "red" "red" "red" "red" "white" "white" "red"
[190] "white" "white" "red" "white" "red" "white" "red" "red" "red"
[199] "red" "red" Nun ziehen wir die ersten 100 Kugeln aus der Urne und lassen die zweiten 100 in der Urne verbleiben:
drawn_balls <- urn[1:100]
drawn_balls [1] "red" "red" "red" "white" "white" "white" "red" "white" "red"
[10] "red" "red" "white" "red" "red" "red" "red" "red" "red"
[19] "red" "red" "red" "red" "red" "white" "white" "red" "white"
[28] "white" "red" "red" "red" "white" "white" "white" "red" "white"
[37] "white" "red" "white" "red" "white" "red" "red" "white" "white"
[46] "red" "white" "red" "white" "red" "white" "white" "red" "white"
[55] "white" "white" "white" "red" "red" "white" "white" "red" "red"
[64] "white" "red" "white" "white" "white" "red" "red" "red" "white"
[73] "red" "red" "white" "white" "red" "white" "white" "white" "red"
[82] "white" "red" "white" "white" "red" "white" "red" "white" "white"
[91] "white" "red" "red" "white" "red" "white" "red" "red" "red"
[100] "red" remaining_balls <- urn[101:200]
remaining_balls [1] "white" "white" "red" "red" "red" "red" "white" "red" "white"
[10] "white" "white" "white" "red" "red" "red" "white" "white" "white"
[19] "white" "red" "red" "red" "red" "red" "red" "red" "red"
[28] "red" "white" "white" "red" "white" "white" "red" "white" "red"
[37] "white" "red" "white" "white" "red" "white" "white" "white" "red"
[46] "red" "white" "white" "red" "white" "white" "white" "white" "white"
[55] "white" "red" "red" "white" "white" "red" "red" "red" "white"
[64] "red" "red" "red" "white" "red" "white" "white" "white" "red"
[73] "red" "red" "white" "red" "white" "red" "red" "red" "red"
[82] "red" "red" "red" "red" "red" "white" "white" "red" "white"
[91] "white" "red" "white" "red" "white" "red" "red" "red" "red"
[100] "red" und zählen, wie viele rote und weiße Kugeln in den beiden Teilvektoren liegen. So erhalten wir eine Vier-Felder-Tafel:
cbind(
drawn = c(
red = sum( drawn_balls=="red" ),
white = sum( drawn_balls=="white" ) ),
remaining = c(
red = sum( remaining_balls=="red" ),
white = sum( remaining_balls=="white" ) ) ) -> mr
mr drawn remaining
red 53 55
white 47 45Was ist das Quotenverhältnis dieser Vier-Felder-Tafel? Wir teilen die Quote der linken Spalte durch die der rechten Spalte:
( mr[1,1] / mr[2,1] ) / ( mr[1,2] / mr[2,2] )[1] 0.9226306Dieses Quotenverhältnis ist näher an der 1 als das Quotenverhältnis, das wir in unserer klinischen Studie hatten:
m drug placebo
improvement 63 45
no improvement 37 55( m[1,1] / m[2,1] ) / ( m[1,2] / m[2,2] ) -> or
or[1] 2.081081Wie oft ist das der Fall?
Wir wiederholen die Simulation 30000 mal und bestimmen jeweils das Quotenverhältnis:
replicate( 30000, {
# Urne füllen
urn <- c( rep( "red", 108 ), rep( "white", 92 ) )
# Urne mischen
urn <- sample( urn )
# Kugeln ziehen
drawn_balls <- urn[1:100]
remaining_balls <- urn[101:200]
# Zählen und Vier-Felder-Tafel aufstellen
cbind(
drawn = c( red = sum( urn[1:100]=="red" ), white = sum( urn[1:100]=="white" ) ),
not_drawn = c( red = sum( urn[101:200]=="red" ), white = sum( urn[101:200]=="white" ) ) ) -> mr
# Quotenverhältnis berechnen
( mr[1,1] / mr[2,1] ) / ( mr[1,2] / mr[2,2] )
}) -> many_null_odds_ratios Hier ist das Histogramm:
hist( many_null_odds_ratios, 300 )
abline( v = c( 1/or, or ), col="darkgreen" )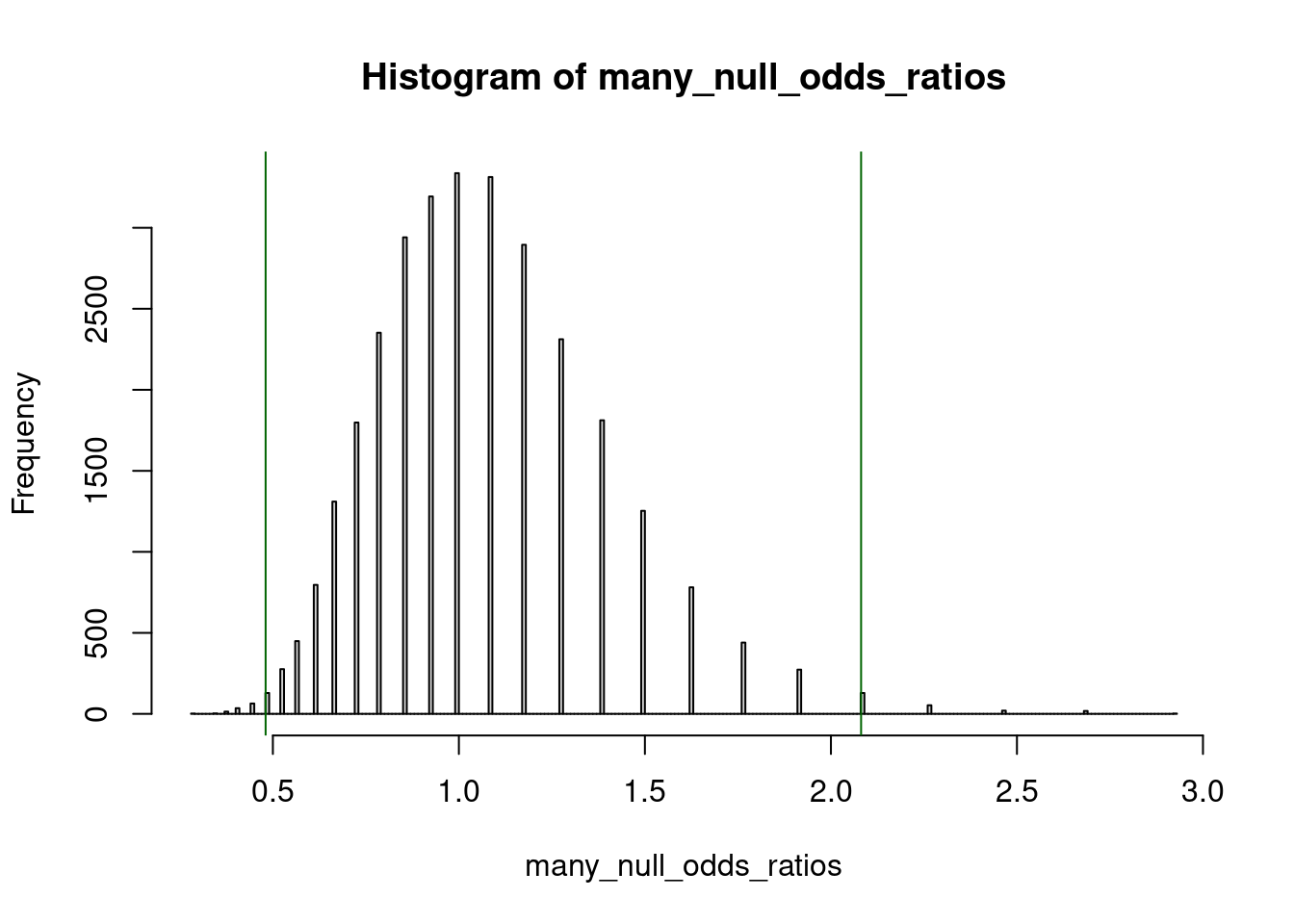
Wenn wir die Werte logarithmieren, wird das Histogramm symmetrisch:
Hier ist das Histogramm:
hist( log2( many_null_odds_ratios ), 300 )
abline( v = log2( c( 1/or, or ) ), col="darkgreen" )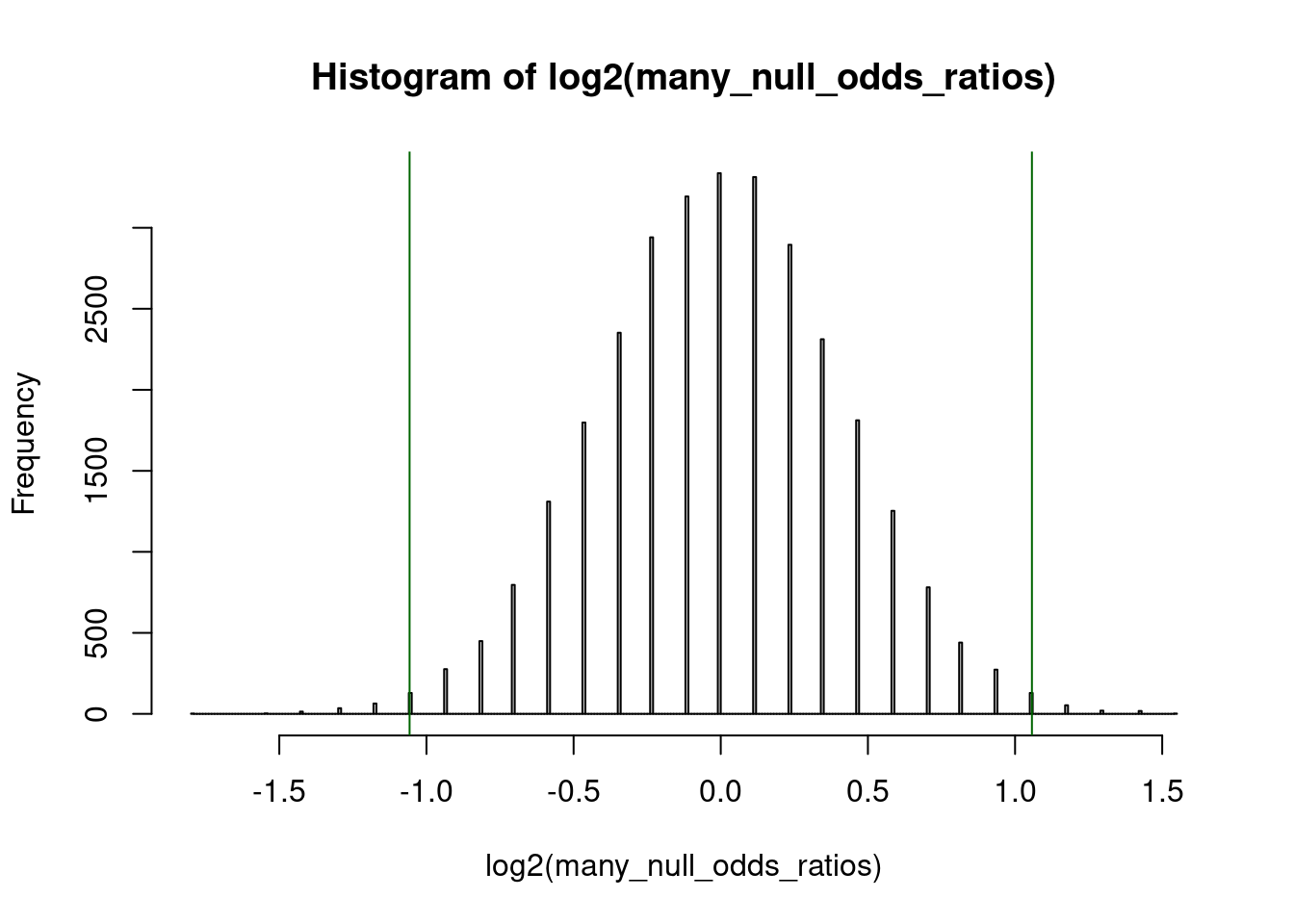
Interpretation:
- Wir haben ein Urnenmodell simuliert, bei dem eine Urne so viele rote Kugeln enthält, wie wir Patienten mit Verbesserung hatten, also 63+45=108 rote Kugel, sowie 37+55=92 weiße Kugeln für die Patienten ohne Verbesserung. Wir haben die Kugeln durch blindes Ziehen aus der Urne aufgeteilt in zwei Gruppen zu je 100 Kugeln, die die beiden Placebo- und Wirkstoff-Gruppe darstellt.
(Anmerkung: Oft spricht man hier vim Ziehen ohne Zurücklegen (drawing without re-placement), da man die gezogene Kugel zur Seite legt, statt sie in die Urne zurück zu legen. Es gibt auch das Urnenmodell mit Zurücklegen, das man in anderen Fällen braucht.)
Dies simuliert die Nullhypothese, dass der Wirkstoff keinen Einfluss auf die Krankheit hat, da wir beim blinden Ziehen (stellt Behandlung mit Wirkstoff dar) nicht bevorzugt rote Kugel (Verbesserung) ziehen können.
Wir erwarten, dass das Verhältnis rote zu weiße Kugeln in beiden Gruppen gleich ist, bzw. um diese Erwartung streut.
Das Doppelverhältnis “rot:weiß in Gruppe gezogen” : “rot:weiß in Gruppe gezogen” sollte also um 1:1 streuen.
Wir haben das Urnenmodell sehr oft simuliert und ein Histogramm dieses Doppelverhältnisses (Quotenverhältnisses) erstellt.
Wie oft weicht das Qotenverhältnis in der Urnensimulation stärker von 1:1 ab als das Quotenverhältnis in unserem Studienergebnis? Wie oft ist es größer als 2.08:1 oder kleiner als 1:2.08? Diese Grenzen haben wir oben im Hostogramm mit grünen Linien markiert.
Wir zählen wie oft der Wert außerhalb des Bereichs liegt
sum( many_null_odds_ratios > or ) + sum( many_null_odds_ratios < 1/or )[1] 340und dividieren durch die Anzahl der Simulationen (30000)
( sum( many_null_odds_ratios > or ) + sum( many_null_odds_ratios < 1/or ) ) / length(many_null_odds_ratios)[1] 0.01133333# dasselbe, anders geschrieben
mean( many_null_odds_ratios > or | many_null_odds_ratios < 1/or )[1] 0.01133333Die Wahrscheinlichkeit, bei unserem Urnenmodell eine Vier-Felder-Tafel mit eiem Quotenverhältnis wie bei unserer Studie zu erhalten oder ein Quotenverhältnis, das noch stärker von 1:1 abweicht, ist also 1,1%.
Das Urnenmodell entspricht unserer Nullhypothese, nämlich dass es keinen Zusammenhang zwischen der Zuweisung (Wirkstoff oder Plazebo) und dem Ergebnis (Verbesserung oder nicht) gibt. Also können wir die Nullhypothese, dass der erprobte Wirkstoff nicht wirkt, mit einem p-Wert von 1,1% zurückweisen (sofern wir 1,1% für einen hinreichend kleinen p-Wert halten).
Rechnen statt Simulieren
Gegeben eine Urne mit 108 roten und 92 weißen Kugeln, aus der blind 100 Kugeln gezogen werden. Wie wahrscheinlich ist es, dass darunter genau 63 rote Kugeln zu ziehen? Dieser Frage beantwortet die sog. hypergeometrische Verteilung
dhyper( 63, 108, 92, 100 )[1] 0.004390518Wie wahrscheinlich ist es, mindestens 63 rote Kugeln zu ziehen. Sie kennen das Muster inzwischen: wir schalten von d auf p
1 - phyper( 63-1, 108, 92, 100 )[1] 0.007827102Dies ist die Wahrscheinlchkeit rechts der rechten grünen Linie. Wenn wir sie verdoppeln, erhalten wir die Wahrscheinlichkeit beider Tails und somit nun durch exakte Rechnung den p-Wert, den wir eben durch Simulation ungefähr bestimmt haben
2* ( 1 - phyper( 63-1, 108, 92, 100 ) )[1] 0.0156542Das ist auch die Rechung, die der Fisher-Test durchführt. Allerdings erwartet er, dass wir die Daten als Vier-Felder-Tafel übergeben:
m drug placebo
improvement 63 45
no improvement 37 55fisher.test( m )
Fisher's Exact Test for Count Data
data: m
p-value = 0.01565
alternative hypothesis: true odds ratio is not equal to 1
95 percent confidence interval:
1.137985 3.813096
sample estimates:
odds ratio
2.07331 Beachten Sie, dass der Fishertest uns auch ein KI füë das Quotenverhältnis liefert.
Nützlicher wäre ein Wert und ein KI für das relative Risiko; darauf wollen wir aber hier nicht eingehen.
Vergleich Bnomialtest vs Fishertest
Mit dem Binomialtest vergleich man den Anteil an “Erfolgen” in einem Experiment mit einer a priori als Nullhypothese vorgegebenen Erfolgswahrscheinlichkeit. Man braucht also drei Werte: Anzxahl der Versuche, Anzahl der Erfolge, Erfolgswahrscheinlichkeit unter der Null. Man möchte feststellen, ob die wahre Erfolgswahrscheinlichkein von der Annahme der Nullhypothese abweicht.
Beim Fisher-Test hat man ein Experiment unter zwei Bedingungen (z.B. behandelt und Kontrolle) durchgeführt, und gezählt, wie viele der Versuche jeweils erfolgreich waren. Man hat also eine Vier-Felder-Tafel mit Anzahl der Erfolge und Fehlschläge in den beiden Gruppen. Man möchte die Nullhypothese verwerfen, dass die Erfolgswahrscheinlichkeit in beiden Gruppen gleich ist, dass also die Behandlung keine Wirkung hat.
Ausblick: Chi-Quadrat-Test
Ohne Computer ist die Durchführung des Fishertests sehr mühsam. Daher versucht man, die hypergeometrische Verteilung durch eine Normalverteilung anzunähern und kommt so zum \(\chi^2\)-Test, den Pearson im Jahr 1900 vorgeschlagen hat. (Historisch war es umgekehrt: Pearson’s Test kam zuerst, Fisher bemerkte dann, dass er sehr ungenau wird, wenn die Zahlen in der Vier-Felder-Tafel klein sind, und schlug seinen Test 1922 vor als “exakte” Alternative.)
Für unsere Zahlen ergeben beide Tests in der Tat fast denselben p-Wert:
chisq.test( m )
Pearson's Chi-squared test with Yates' continuity correction
data: m
X-squared = 5.8172, df = 1, p-value = 0.01587Mit dem Computer geht beides schnell; ohne Computer (also nur mit Papier, Bleistift und Tabellen) lässt sich nur Pearsons Test praktisch durchführen.
Ein Vorteil des \(\chi^2\)-Tests ist, dass er sich leicht für den Fall verallgemeinern lässt, dass die Kreuztabelle mehr als vier Felder hat, weil man mehr als zwei Ergebnisse oder mehr als zwei Versuchsgruppen hat.
Aufgabe
Wie Sie sich sicher erinnern, wurden die Covid-Impfstoffe im Jahr 2020 erprobt und dann zugelassen, nachdem ihre Wirksamkeit gezeigt werden konnte. Das Team von BionTech und Pfizer veróöffentlichte die Daten ihrer Studie hier:
Polack et al.: Safety and Efficacy of the BNT162b2 mRNA Covid-19 Vaccine. N Engl J Med 2020; 383:2603-2615. doi:10.1056/NEJMoa2034577
Entnehmen Sie dem Abstract die Anzahl der Probanden in Impfstoff- und Plazebo-Gruppe und die Anzahl der Probanden in den jeweiligen Gruppen, die sich nach Ablauf der Beobachtungsperiode infiziert hatten. Führen Sie einen Fisher-Test durch, bestimmen und interpretieren Sie den p-Wert und das KI. Welche Nullhypothese untersuchen Sie hierbei genau?