Experimente mit dem Zufall

Vorlesung “Datananalyse in der Biologie”

Zufallszahlen

Statistik ist oft nicht intuitiv. Man kann aber eine Intuition aufbauen, in dem man “Experimente” am Computer durchführt.

Wichtigstes Werkzeug hierzu ist der Pseudo-Zufallsgenerator (pseudo-random number generator, PRNG oder RNG). Das ist eine Funktion, die ein “zufällige” Zahl zwischen 0 und 1 erzeugt:

runif(1)

[1] 0.5427997

Jedes Mal, wenn man die Funktion aufruft, erhält man eine andere Zufallszahl

runif(1)

[1] 0.4510996

Man kann sich auch einen ganzen Vektor mit Zufallszahlen geben lassen:

runif(15)

 [1] 0.9838402 0.2936511 0.9665711 0.8178740 0.9054709 0.4594896 0.6042096
 [8] 0.2454899 0.1285700 0.9984228 0.2069635 0.6420391 0.4828940 0.5866124
[15] 0.6748902

Die Zahlen sind aber nicht wirklich zufällig, da ein Computer strengt deterministisch arbeitet. Der PRNG hat einen Zustand (einen Satz an Zahlen), die bei jedem Aufruf durch eine kompliziertes Verfahren in einen neuen Zustand umgerechnet werden. Das verfahren ist so konstruiert, dass der Zusammenhang aufeinanderfolgenden Zustände so “verworren” ist, dass man ihn auch nach komplizierten Verfahren nicht nachvollziehen kann. Das Verfahren, dass R by default verwendet, ist der sog. Mersenne-Twister.

Aus den Zahlen, die den Zustand bilden, wird jeweils eine Zahl ermittelt, die im Einheitsinterval gleichverteilt ist (d.h., jede Zahl zwischen 0 und 1 hat dieselbe Wahrscheinlichkeit).

Der Random Seed

Man kann den PRNG neu initialisieren, indem man eine beliebige Zahl (genannt random seed) übergibt, aus der dann der Zustand gewonnen wird:

set.seed( 13572468 )
runif( 15 )

 [1] 0.3740267 0.2446231 0.9421103 0.7831750 0.4812258 0.4514881 0.9826566
 [8] 0.6460481 0.4141595 0.2147015 0.3819205 0.5862113 0.7767019 0.3161018
[15] 0.9519008

Wenn man ein zweites Mal denselben Seed setzt, erhält danach jeweils dieselben Zufallszahlen wie beim ersten Mal:

set.seed( 13572468 )
runif( 10 )

 [1] 0.3740267 0.2446231 0.9421103 0.7831750 0.4812258 0.4514881 0.9826566
 [8] 0.6460481 0.4141595 0.2147015

runif( 10 )

 [1] 0.381920465 0.586211259 0.776701877 0.316101774 0.951900829 0.234656146
 [7] 0.822471993 0.826193840 0.397526995 0.005772249

Bei jedem Neustart erzeugt sich R einen Random-Seed, indem es die aktuelle Zeit (in Millisekunden seit dem 1. Januar 1980, glaube ich) und die Prozess-ID zusammensetzt. Somit wird R praktisch nie zweimal mit demselben Seed starten, und die generierten Zufallszahlen erscheinen stets zufällig.

Wenn man aber eine Analyse mit Zufallszahlen “reproduzierbar” machen will, empfiehlt es sich, einen Seed zu setzen.

Zufällige Punkte

Als erstes Beispiel erzeugen wir und 2 Vektoren zu je 10.000 Zufallszahlen, die wir x und y nennen und in eine Tabelle schreiben:

suppressPackageStartupMessages( library(tidyverse) )

tibble( 
  x = runif( 10000 ),
  y = runif( 10000 ) ) -> random_points

Wir verwenden head, um die ersten 10 Zeilen dieser langen Tabelle ausgeben zu lassen:

head( random_points )

# A tibble: 6 × 2
       x     y
   <dbl> <dbl>
1 0.406  0.103
2 0.0194 0.781
3 0.707  0.967
4 0.0879 0.295
5 0.820  0.629
6 0.298  0.569

Wir betrachten die Zahlen als x- und y-Koordinate von 10.000 Punkten, die wir plotten:

Aufgabe: Erstellen Sie den Plot.

Der Punkt in der Mitte des Plots hat die Koordinaten x=0,5, y=0,5. Wir berechnen mit dem Satz des Pythagoras den Abstand jedes Punktes zum Mittelpunkt.

Aufgabe: Fügen Sie eine Spalte distance_to_midpoint hinzu. Fügen Sie dann eine weiter Spalte in_circle hinzu, die TRUE enthält, wenn der Abstand zu Mitte kleiner ist als 0,5, sonst FALSE.

# A tibble: 6 × 4
       x     y distance_to_midpoint in_circle
   <dbl> <dbl>                <dbl> <lgl>    
1 0.406  0.103                0.408 TRUE     
2 0.0194 0.781                0.557 FALSE    
3 0.707  0.967                0.511 FALSE    
4 0.0879 0.295                0.460 TRUE     
5 0.820  0.629                0.346 TRUE     
6 0.298  0.569                0.213 TRUE

Hier ist ein Plot, indem die Punkte nach der Spalte in_circle eingefärbt sind:

random_points_circled %>%
ggplot( aes( x=x, y=y, col=in_circle ) ) + 
  geom_point( size=.1 ) +
  coord_equal()

Wie viele der Punkte sind im Kreis?

Wir überlegen erst, was wir erwarten: Das Quadrat hat die Fläche 1. Der Kreis hat den Radius \(r=\frac{1}{2}\) und somit die Fläche \(A=r^2\pi=\frac{\pi}{4}\):

pi/4

[1] 0.7853982

Somit sollten 78.54% der 10,000 Punkte, also 7854 Punkte, im Kreis liegen.

Aufgabe: Zählen Sie

random_points_circled %>%
group_by( in_circle ) %>%
summarise( n() )

Wir können auch direkt den Anteil der Punkte berechnen:

random_points_circled %>%
summarise( fraction_in_circle = mean( in_circle ) ) %>%
mutate( pi_estimate = 4 * fraction_in_circle )

Hier haben wir die Funktion “mean” auf eine boolsche (logische) Spalte angewendet. Wenn man mit boolschen Werten (d.h. FALSE und TRUE) rechnet, wird FALSE als 0 und TRUE als 1 gewertet. Die Summe sum(in_circle) ist also die Anzahl der TRUE-Werte, und der Mittelwert mean(in_circle) folglich diese Anzahl, geteilt durch die Gesamtzahl an Tabellen-Zeilen.

In der letzten Zeile nehmen wir den Anteil mal 4, und erhalten so einen “Schätzwert” für \(\pi\).

Ein mathematisches Experiment

Man kann dies auch als eine Methode ansehen, den Wert der Kreiszahl \(\pi\) auf experimentelle Weise zu bestimmen: Markieren Sie auf einem großen Platz im Freien ein Quadrat auf dem Boden. Markieren Sie auch den dem Quadrat einbeschriebenen Kreis. Warten Sie auf einen leichten Regenschauer. Zählen Sie, wie viele Regentropfen in das Quadrat gefallen sind und welcher Anteil davon innerhalb des Kreises liegt. Multiplizieren Sie den Anteil mit 4. Das ist Ihr experimenteller Wert für \(\pi\).

Wie genau können wir \(\pi\) auf diese Weise ermitteln?

Wie hängt dies von der Anzahl der Regentropfen bzw. der Größe des Quadrats ab?

Wie können wir wissen, wie genau unser experimentel ermittelter Schätzwert für \(\pi\) ist, wenn wir den wahren Wert von \(pi\) nicht wissen?

Über solche Fragen nachzudenken, hilft uns, das Wesen der inferentiellen Statistik zu verstehen.

Der Vorteil dieses Experiments gegenüber “echten” Experimenten:

Wir wissen, was die exakte Lösung ist:

pi

[1] 3.141593

Wir können das Experiment mühelos beliebig oft durchführen. Statt auf echten Regen zu werten, benuzten wir einfach unseren Zufallszahlen-Generator.

Diese Methode, Experimente zu simulieren, ist sehr wertvoll, um die Grenzen quantitativer Experimente zu verstehen.

Funktionen

Bevor wir fortfahen, brauchen wir ein neues Instrument in R: selbst-definierte Funktionen.

Hier ist ein Beispiel:

add_two <- function( x ) {
  x + 2
}

Hier haben wir eine neue Funktion definiert, die man genauso aufrufen kann wie normale Funktionen:

add_two( 10 )

[1] 12

add_two( -3.7 )

[1] -1.7

Bei jedem Aufruf wird der Code, den wir oben in geschweiften Klammern eingegeben haben, ausgeführt. Vorher wird jeweils der Wert, der in den runden Klammern übergeben wurde, für x eingesetzt.

Wir schauen uns die Einzelteile der Funktions-Definition nochmal genau an:

add_two <- function( x ) {
  x + 2
}

add_two ist der Name, mit dem wir die Funktion danach aufrufen können.
Dem Namen folgt der Zuweisungspfeil <-, den wir schon von Variablen kennen. Er zeigt, wie auch bei Variablen, stets zum Namen hin.
Dann kommt das Schlüsselwort (key word) function, das den Code zur Funktions-Definition macht.
Dem folgt die Argumentsliste in runden Klammern. Unsere Argumentsliste enthält nur ein Argument, x. Wir nenen das x hier ein formelles Argument (formal argument), da es lediglich Platzhalter für einen noch einzusetzenden Wert ist.
Dann folgt der Funktionskörper (function body). Er ist in geschweifte Klammern (curly braces, { und }) eingeschlossen. Der Code innerhalb der geschweiften Klammern wird jedes Mal ausgeführt, wenn die Funktion aufgerufen wird. Dabei wird jedes Vorkommen der funktionalen Arguments x durch den eingesetzten Wert ersetzt.
Wenn der Funktionskörper nur eine einzige Anweisung enthält, dürfen die geschweiften Klammern auch weggelassen werden.

Nun sehen wir uns einen Funktionsaufruf genauer an:

add_two( 10 )

[1] 12

Der Aufruf besteht aus dem Namend er Funktion, gefolgt von runden Klammen, die die Argumentsliste enthält. Unsere Funktions-Definition hatte nur ein formelles Argument, x, für das nun eie konkreter Wert (actual argument), 10, eingesetzt wird.
Nun wird der Funktionskörper, also die Anweisungen innerhalb der geschweiften Klammern, ausgeführt. Innerhalb des Funtionskörpers verhält sich das formale Argument x wie eine Variable, die diesmal den Wert 10 hat.
Das Ergebnis der Anweisungen im Funktionskörper (hier: x+2), hier also der Wert 22, ist der Rückgabe-Wert (return value) der Funktion.
Man kann den Rückgabe-Wert in weiteren Rechnungen verwenden:

add_two( 10 ) * 3

[1] 36

Scoping

Das formale Argument x existiert nur innerhalb des Funktionskörpers. Außerhalb ist es nicht bekannt:

x

Error: object 'x' not found

(In der Fachsprache der Informatik sagt man: x ist nur innerhalb von add_two in scope.)

Falls es zufällig auch eine Variable x gibt, so wird diese “ausgeblendet”, während die Funktion ausgefürt wird:

x <- 15

add_two( 30 )

[1] 32

Während add_two lief, hatte x also vorübergehend den übergebenen Wert 30.

Danach hat x aber wieder seinen vorherigen Wert 15:

[1] 15

Diesen Mechanismus nennt man in der Informatik Scoping.

Aufgabe

Schreiben Sie eine Funktion, die drei formale Argumente a, b, und c hat, und die quadratische Gleichung \(a x^2 + bx + c = 0\) löst. Ihre Funktion sollte dazu die Lösungsformel \(x_1 = \frac{ -b + \sqrt{ b^2 - 4ac }}{2a}\) berechnen.

Erweitern Sie dann die Funktion, so dass Sie auch \(x_2 = \frac{ -b - \sqrt{ b^2 - 4ac }}{2a}\) berechnen, und setzten Sie daraus den Lösungsvektor c( x1, x2 ) zusammen, den Sie dann als return value zurück geben.

Testen Sie Ihre Funktion mit \(a=2\), \(b=5\), \(c=-2\). Was geschieht, wenn Sie stattdessen \(c=2\) oder \(c=0\) verwenden?

Wiederholte Zufallsexperimente

Hier ist nochmal der Code, um unser “Experiment” zur Bestimmung von \(\pi\) durchführen

tibble( 
  x = runif( 10000 ),
  y = runif( 10000 ) ) %>%
mutate( distance_to_middle = sqrt( (x-.5)^2 + (y-.5)^2 ) ) %>%
mutate( in_circle = distance_to_middle < .5 ) %>%
summarise( fraction_in_circle = mean( in_circle ) ) %>%
mutate( estimate_for_pi = fraction_in_circle * 4 ) %>%
pull( estimate_for_pi )

[1] 3.1552

Hier ist eine Kleinigkeit neu: Am Ende habe ich eine neue Tidyverse-Funktion eingeführt: pull zieht aus einer Tabelle eine einzelne Spalte heraus. Man erhält diese Spalte als Vektor (mit hier nur einem Wert), der Rest der Tabelle wird verworfen.

Aufgabe Definieren Sie mit diesem Code eine Funktion estimate_pi( n_points ), die als Argument die Anzahl der Punkte (bisher 10000) erwartet.

Wenn wir diese Funktion aufrufen, wird eine Simulation unseres Experiments durchgeführt – hier mit 10000 Regentropfen:

estimate_pi( 10000 )

[1] 3.1448

Da diese Funktion in ihrem Funktionskörper (Pseudo-)Zufallszahlen verwendet, bekommen wir bei jedem Aufruf ein leicht anderes Ergebnis:

estimate_pi( 10000 )

[1] 3.1464

estimate_pi( 10000 )

[1] 3.144

Wir können die R-Funktion replicate verwenden, um unser simuliertes Experiment 20-mal zu replizieren:

replicate( 20, { estimate_pi( 10000 ) } )

 [1] 3.1428 3.1372 3.1904 3.1316 3.1532 3.1484 3.1420 3.1416 3.1564 3.1388
[11] 3.1428 3.1496 3.1528 3.1476 3.1320 3.1584 3.1380 3.1800 3.1240 3.1620

Diese Funktion hat nun den in geschweiften Klammen angefürten Code 20-mal ausgeführt, und die Ergebnisse in einen Vektor zusammen gefasst. Jedes dieser 20 Durchgänge generierte jeweils 10000 zufällige Punkte.

Eine empirische Stichproben-Verteilung

Wir lassen unseren Computer dies nun 1000-mal machen:

many_estimates <- replicate( 1000, { estimate_pi( 10000 ) } )

Hier ist nun ein Histogramm der Ergebnisse dieser 1000 simulierten Experimente. Eine violette Linie markiert den echten Wert von \(\pi\).

tibble( many_estimates ) %>%
ggplot( aes( x=many_estimates ) ) +
  geom_histogram() +
  geom_vline( xintercept = pi, col="purple" ) +
  scale_x_continuous( breaks=seq( 3.07, 3.2, by=0.01) )

`stat_bin()` using `bins = 30`. Pick better value with `binwidth`.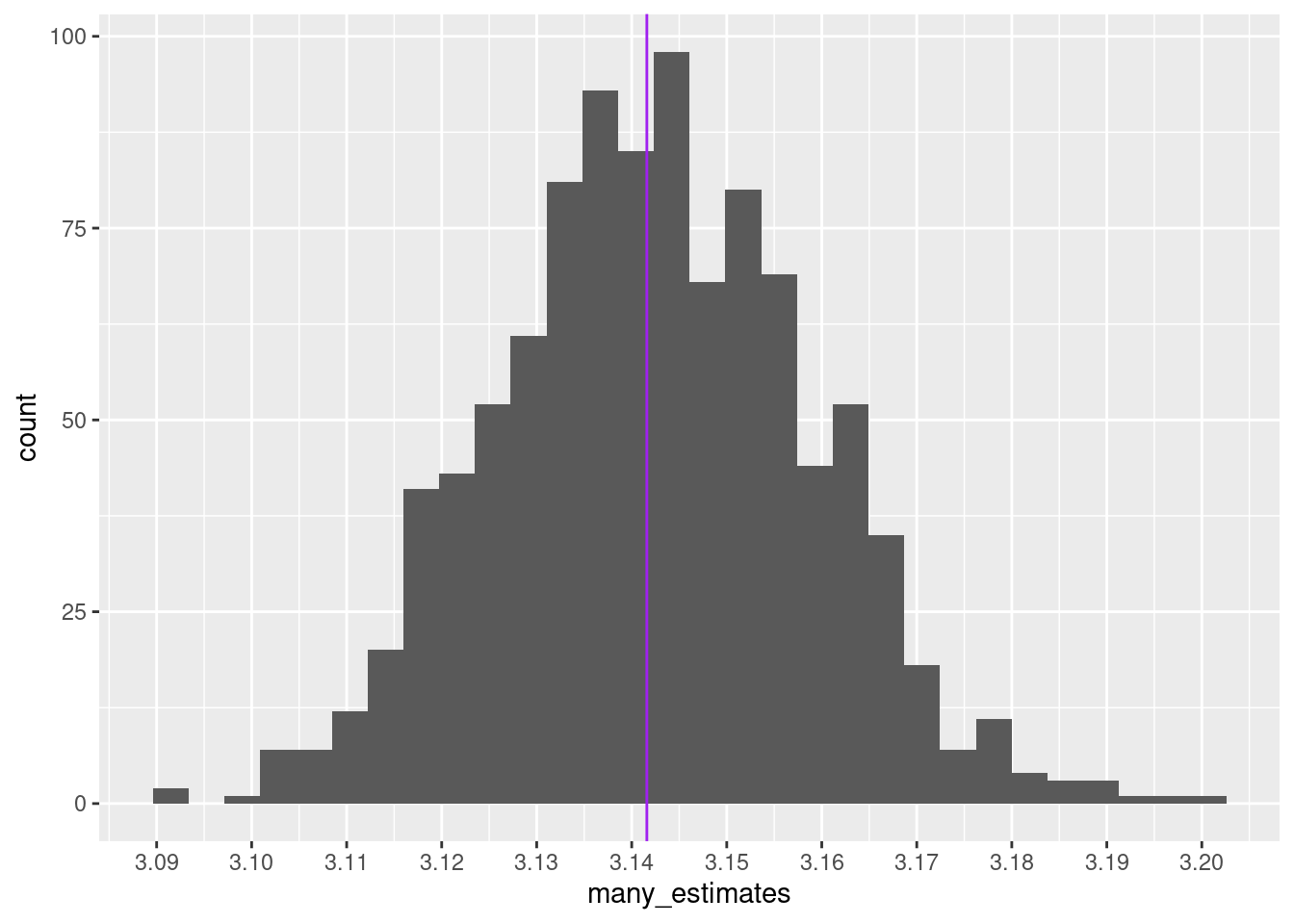

Wir charakterisieren diese Verteilung nun, indem wir einige simple Statistiken berechnen:

Zunächst der Mittelwert:

mean( many_estimates )

[1] 3.142258

Nun die Standardabweichung:

sd( many_estimates )

[1] 0.01657951

Diese Standardabweichung können wir als eine “typischen” Wert interpretieren, wie weit ein “Messergebnis” unseres Experiments (nämlich, einmal 10000 Regentropfen durchzuzählen) vom “wahren Wert” abweicht. Man kann sagen: Die Standardabweichung dieser Verteilung ist der Standardfehler, den wir bei diesem Experiment erwarten sollten.

Hier sehen wir sofort ein offensichtliches Problem: In Wirklichkeit führen wir ein Experiment nur einmal durch, nicht etwa 1000 mal. Die Verteilung, die das eben gezeichnete Histogramm darstellt, steht uns “im echten Leben” nicht zur Verfügung. Wie können wir dennoch abschätzen, wie breit sie ist oder wie groß der Standardfehler ist?

Diese Frage für ein gegebenes experimentelles Design zu beantworten ist die Kernaufgabe der sog. inferentiellen Statistik.

Ein experimentelles Ergebnis ist nutzlos, wenn man nicht zumindest abschätzen kann, wie genau es ist! Daher ist inferentielle Statistik von größter Wichtigkeit für alle empirische Forschung.

Andere Wege, die Breite einer Verteilung zu beschreiben

Da die Standardabweichung ein manchmal etwas abstrakted Maß ist, woleln wir noch eine Alternative erwähnen, die sogenannten Quantile:

quantile( many_estimates, c( 0.1, 0.9 ) )

   10%    90% 
3.1208 3.1636

Dies bedeutet: 10% der Werte in many_estimate sind kleiner als 3.1208 und 90% der Werte in many_estimate sind kleiner als 3.1636.

Das macht mehr Sinn, wenn man es so formuliert: 80% der Werte liegen im Bereich 3.1208 bis 3.1636, 10% darunter und 10% darüber.

Man nennt diese beiden Werte das 0.1-Quantil und das 0.9-Quantil, oder auch das 10-Perzentil und das 90-Perzentil. Die dazwischen liegende Spanne hat die Breite

quantile( many_estimates, .9 ) - quantile( many_estimates, .1 )

   90% 
0.0428

und dies können wir, ebenso wie die Standardabweichung, als Maß für die Breite unserer Verteilung, und somit für die Genauigkeit unseres Experiments nehmen.

Hausaufgabe

(1.) Führen Sie den Code, um unser Experiment 1000 mal durchzuführen, nochmals durch. Erhalten Sie in etwa die gleichen Werte für die Breite der Verteilung wie in der Vorlesung? Sind 1000 Wiederholungen also ausreichend, um die Breite zu bestimmen?

(2.) Unser experimenteller Mathematiker war sehr fleißig: Er oder sie hat ein Quadrat mit 10,000 Regentropfen durchmustert, um zu bestimmen, wie viele davon im Inkreis liegen und wurde dafür mit einem Schätzwert für die Kreiszahl \(\pi\) belohnt, von dem er/sie erwarten darf, dass die Abweichung des Wert vom wahren Wert in der Größenordnung unsere oben ermittelte Standardabweichung von nur 0.017 liegt.

Wie genau wäre das Ergbnis, wenn man nur 1000 Tropfen durchzählt? Bestimmen Sie die Standard- Abweichung der Verteilung der simulierten Mess-Ergebnisse für simulierte Experimente mit nur je 1000 Tropfen.

Wie sieht es mit nur 100 oder gar nur 10 Tropfen aus? Erstellen Sie eine Tabelle mit der Tropfenzahl (10000, 1000, 100, 10) und ihrer Standardabweichung der Messwerte.

(3.) Visualisieren Sie Ihre Tabelle als Streudiagramm (mit 4 Datenpunkten). Plotten Sie dazu die Standardabweichung gegen die Tropfenzahl. Stellen Sie beide Achsen logarithmisch dar. Können Sie einen mathematische Zusammenhang zwischen Tropfenzahl und Genauigkeit erraten?

-> Bitte laden Sie Code, Tabelle und Plot auf Moodle hoch.