Konfidenzintervalle für Mittelwerte

Vorlesung “Datenanalyse in der Biologie”

Beispiel und Problemstellung

Bevor wir zur genauen Definition von Konfidenzintervallen betrachten, betrachten wir ein Beispiel. Wieder nehmen wir an, dass die Körpergröße aller erwachsenen männlichen Einwohner in Deutschland durch eine Normalverteilung beschriebven werden kann mit Mittelwert 178 cm und Stndardabweichung 7cm.

Wir nehmen an, ein Statistiker, der diese Werte nicht kennt, möchte sie ermitteln und erhabt dazu eine Stichprobe von 100 Männern:

suppressPackageStartupMessages( library(tidyverse) )

height_sample <- rnorm( 100, mean=178, sd=7 )

Der Mittelwert der Stichprobe ist

sample_mean <- mean( height_sample )

und unser Statistiker ermittelt auch noch die Stnadardabweichung

sd( height_sample )

[1] 7.68541

und daraus eine Schätzung des Standardfehlers des Mittelwerts:

sem <- sd( height_sample ) / sqrt(100)
sem

[1] 0.768541

Unser Statistiker gibt nur das Ergebnis als Mittelwert plus/minus STandardfehler an, also

c( sample_mean - sem, sample_mean + sem )

[1] 177.9343 179.4714

und behauptet, der wahre Wert liege in diesem Interval. Wie oft liegt er mit dieser Behauptung wohl richtig?

Dazu simulieren wir diese Erhebung 3000-mal:

replicate( 3000, {
   height_sample <- rnorm( 100, mean=178, sd=7 )
   sample_mean <- mean( height_sample )
   sem <- sd( height_sample ) / sqrt(100)
   c( lower = sample_mean - sem, upper = sample_mean + sem )
}) %>% 
t %>% as_tibble() -> many_intervals

many_intervals

# A tibble: 3,000 × 2
   lower upper
   <dbl> <dbl>
 1  178.  179.
 2  177.  179.
 3  176.  177.
 4  179.  180.
 5  178.  180.
 6  178.  179.
 7  177.  179.
 8  178.  179.
 9  179.  180.
10  177.  178.
# ℹ 2,990 more rows

Wie oft liegt der wahre Wert (178 cm) im Interval?

many_intervals %>%
mutate( contains_true_value = lower < 178 & upper > 178 ) %>%
summarise( mean( contains_true_value ) )

# A tibble: 1 × 1
  `mean(contains_true_value)`
                        <dbl>
1                       0.677

Nach der 68-95-99,7-Regel erwarten wir, dass ein Interval, das mit dem einfachen Standardfehler gebildet wird, den wahren Wert in 68% der Fälle enthält. Das bestätigt sich hier.

68% reicht uns aber nicht. Wir hätten lieber 95%. Dafür brauchen wir zwei Standardabweichungen:

c( sample_mean - 2*sem, sample_mean + 2*sem )

[1] 177.1658 180.2399

Wir simulieren auch das, mit demselben Code wie eben, aber mit 2*sem statt sem:

replicate( 3000, {
   height_sample <- rnorm( 100, mean=178, sd=7 )
   sample_mean <- mean( height_sample )
   sem <- sd( height_sample ) / sqrt(100)
   c( lower = sample_mean - 2*sem, upper = sample_mean + 2*sem )
}) %>% 
t %>% as_tibble() %>%
mutate( contains_true_value = lower < 178 & upper > 178 ) %>%
summarise( mean( contains_true_value ) )

# A tibble: 1 × 1
  `mean(contains_true_value)`
                        <dbl>
1                       0.956

Es funktioniert: Wenn wir das Interval bilden, indem wir Mittelwert plus/minus doppelter Standardfehler rechnen, erhalten wir eine Überdeckung des wahren Werts in 95% der Versuche.

kleine Haarspalterei: Die Wahrscheinlichkeit, dass ein aus einer Normalverteilung gezogener Wert höchstens die doppelte Standardabweichung vom Mittelwert abweicht, ist nicht 95% sondern 95.4%:

pnorm(2) - pnorm(-2)

[1] 0.9544997

Um genau 95% zu erhalten, sollte man daher genau genommen nicht mit 2 multiplizieren, sondern mit 1.96.

pnorm(1.96) - pnorm(-1.96)

[1] 0.9500042

Den Wert 1.96 kann man auch folgendermaßen bestimmen: Wir benötigen die Quantile der Standard-Normalverteilung zu 2.5% und 97,5%, denn zwischen diesen liegen 95% der Werte:

qnorm(0.975)

[1] 1.959964

qnorm(0.025)

[1] -1.959964

Ende der Haarspalterei

Definition Konfidenzinterval

Was wir eben berechnet haben, nennt man ein 95%-Konfidenzinterval (95% confidence interval, 95%-C.I.).

Wenn zu einem Ergebnis ein solches Interval angegeben und als 95%-Konfidenzinterval bezeichnet wird, so bedeutet das: Dieses Interval wurde mit einem Verfahren berechnet, dass mit mindestens 95% Wahrscheinlichkeit ein Interval ergibt, dass den wahren Wert enthält.

Konfidenzintervalle für Mittelwert: das (zu) einfache Verfahren

WIr haben eben ein Verfahren gesehen, um ein 95%-KI für Mittelwerte zu berechnen: Nimm den Stichproben-Mittelwert plus/minus 2-mal der Standardfehler dieses Mittelwerts.

Dieses Verfahren ist einfach, funktioniert aber nicht mehr, wenn die Stichprobe klein ist.

Um das zu zeigen, lassen wir den Code von eben nochmal laufen, ziehen diesmal aber nur 8 Männer pro Stichprobe:

replicate( 3000, {
   height_sample <- rnorm( 8, mean=178, sd=7 )   # <- hier 10 statt 100
   sample_mean <- mean( height_sample )
   sem <- sd( height_sample ) / sqrt(8)
   c( lower = sample_mean - 2*sem, upper = sample_mean + 2*sem )
}) %>% 
t %>% as_tibble() %>%
mutate( contains_true_value = lower < 178 & upper > 178 ) %>%
summarise( mean( contains_true_value ) )

# A tibble: 1 × 1
  `mean(contains_true_value)`
                        <dbl>
1                       0.914

Statt 95% ist die Überdeckungswahrscheinlichkeit nun unter 50%. Was ist jetzt schief gelaufen?!

Mit dieser Frage hat sich William Gosset, Chef-Brauer bei Guiness und Statistiker, um 1920 beschäftigt und dazuu unter dem Pseudonym “Student” publiziert.

Das Problem: Die Formel für den Standardfehler des Mittelwerts, \(\text{SEM}=\text{SD}/sqrt{n}\), gilt eigentlich nur, wenn man für \(\text{SD}\) die “wahre” Standardabweichung der Grundgesamtheit einsetzt. Wenn \(n\) groß ist, weicht die Standardabweichung der Stichprobe kaum von der Standardabweichung der Grundgesamtheit ab. Bei kleinem \(n\) kann man die Standardabweichung aber leicht drastisch unterschätzen, was die Berechnung des Konfidenzintervalls ungültig macht.

Die einfache Formel für den Standardfehler des Mittelwerts, \(\text{SEM}=\text{SD}/sqrt{n}\), liefert kein verlässliches Ergebnis, wenn der Stichproben-Umfang \(n\) zu klein ist, um aus der Stichprobe eine hinreichend genaue Schätzung für \(\text{SD}\) zu erhalten.

Zum Glück hat Gosset/Student eine Lösung füë das Problem gefunden, die Student’sche t-Verteilung.

Student-t-Verteilung

Wir machen folgendes Experiment: Wir ziehen \(n=100\) Werte aus einer Standard-Normalverteilung, bestimmen Mittelwert und Standardabweichung. Dann teilen wir den geschätzten Mittelwert durch die geschätzte Standardabweichung. Dies führen wir sehr oft (30000 mal) durch, um die sampling distribution zu erhalteb. Wenn die geschätzte Standardabweichung exakt wäre (also genau 1), dann sollten wir eine Normalverteilung mit Mittelwert 0 und Standardabweichung \(1/\sqrt{n}=0.1\) erhalten.

n <- 100

replicate( 30000, {
  sample <- rnorm( n )
  mean( sample ) / sd( sample )
} ) -> many_estimates

# Plot histogram
hist( many_estimates, breaks=100, freq=FALSE )

# Plot density of normal with mean 0 and SD 1/sqrt(n)
xg <- seq( -.4, .4, length.out=1000 )
lines( x = xg, y = dnorm( xg, sd=1/sqrt(n) ), col="magenta" )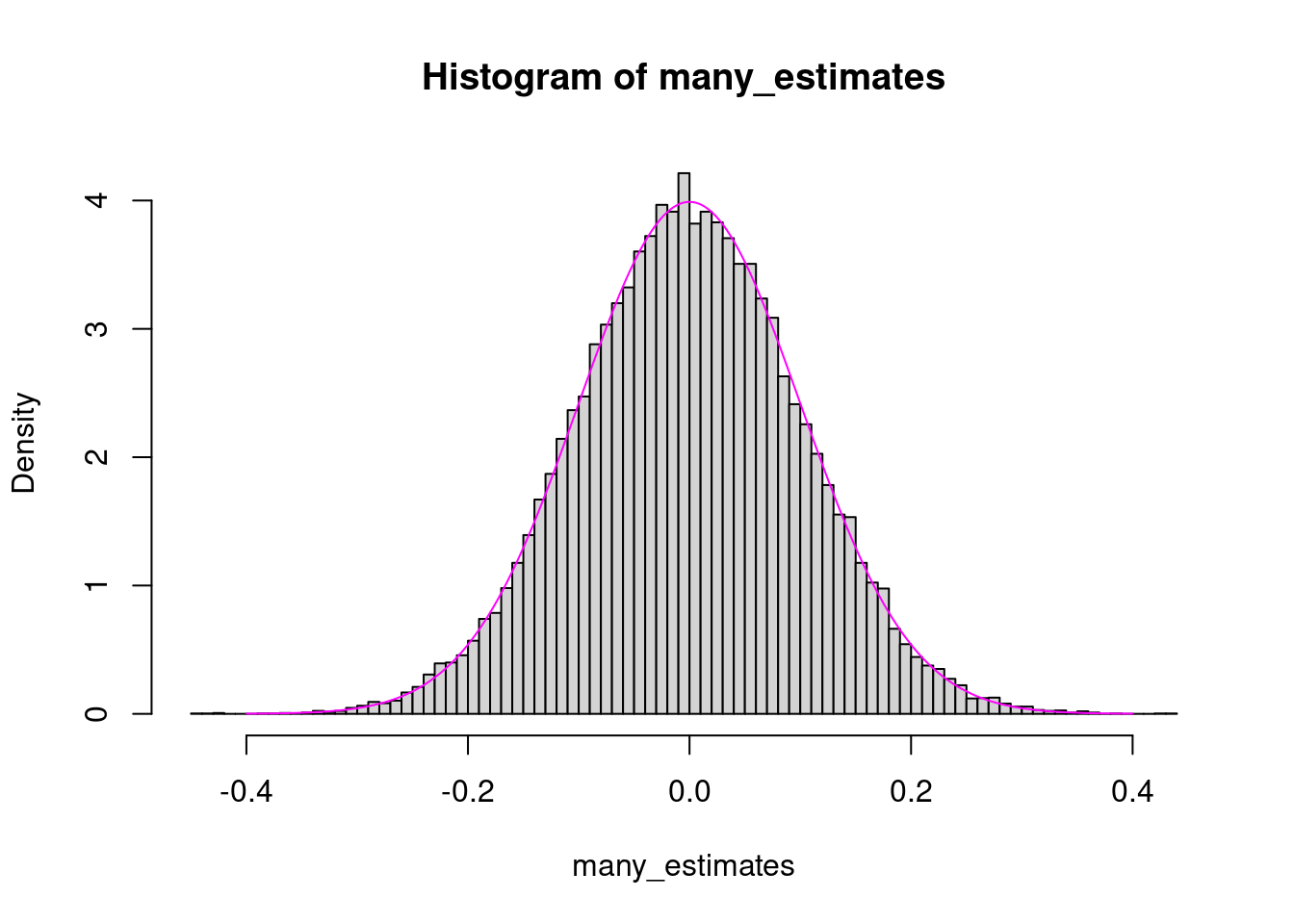

Mit nur 5 Werten pro Stichprobe klappt das nicht mehr so gut:

n <- 5

replicate( 30000, {
  sample <- rnorm( n )
  mean( sample ) / sd( sample )
} ) -> many_estimates

# Plot histogram
hist( many_estimates, breaks=300, freq=FALSE, 
  xlim=c(-3,3), ylim=c(0,.9) )

# Plot density of normal with mean 0 and SD 1/sqrt(n)
xg <- seq( -2, 2, length.out=1000 )
lines( x = xg, y = dnorm( xg, sd=1/sqrt(n) ), col="magenta" )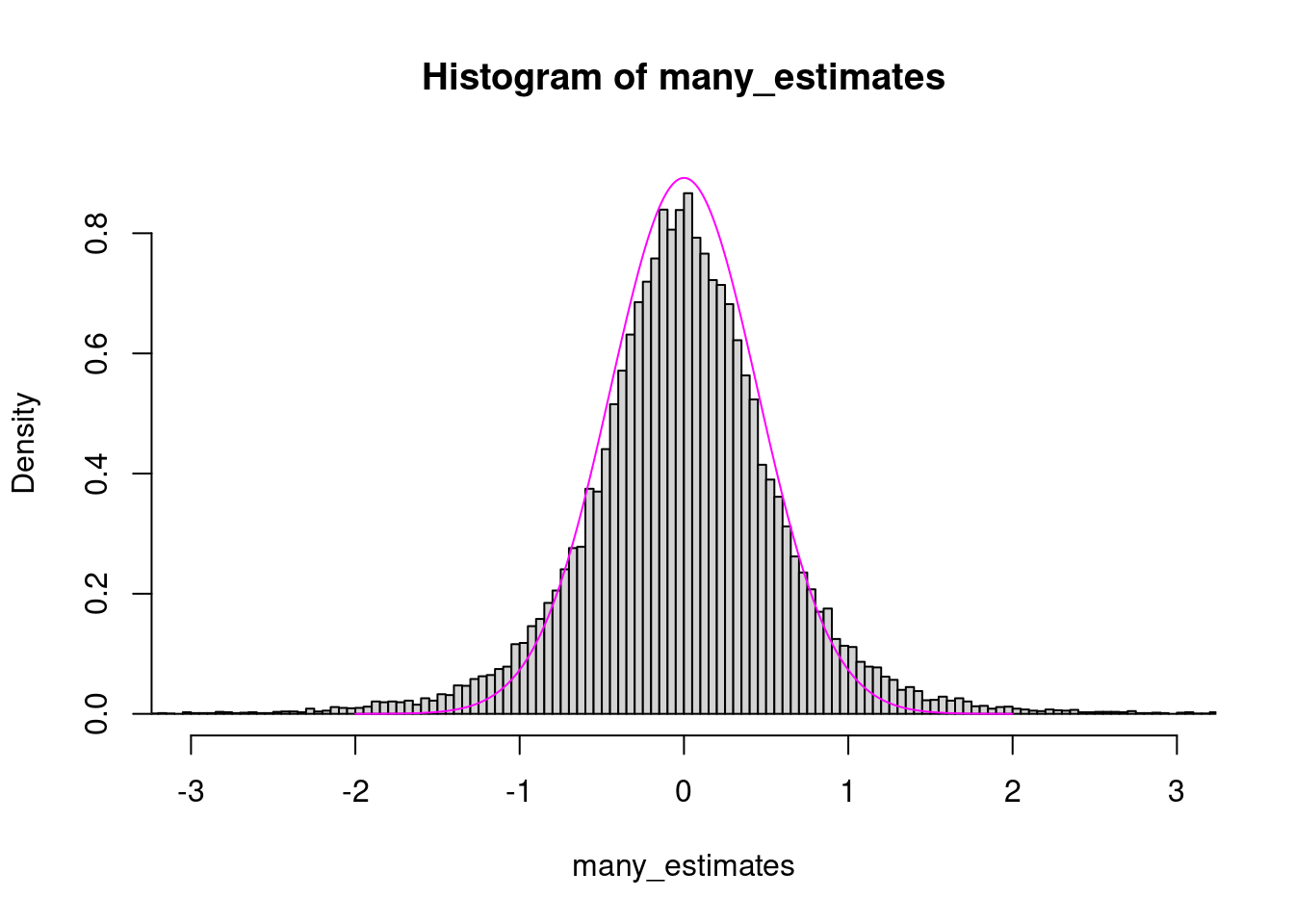

Wir sehen, dass das Teilen durch die geschätze Standardabweichung dazu führt, dass betragsmäßig große Werte häufiger sind als von der Normalverteilung angenommen. Die Glocke hat einen dickeren Rand. (Man sagt: “The tails are fatter than in a normal distribution” oder “There is excess kurtosis.”)

Das führt dazu, dass man das Konfidenzinterval breiter machen muss, als von der 68-95-99,7-Regel vorgegeben, wenn man 95% der Werte einschließen will.

Das Histogramm folgt nicht mehr der Gaußschen Glockenform eine Normalverteilung und die Formel für die Dichte der Normalverteilung passt nicht mehr. Student konnte die passende Formel finden, die Studentsche t-Verteilung.

Hier ist derselbe Plot wie eben noch mal, aber mit Student’s Verteilung ergänzt:

n <- 5

replicate( 30000, {
  sample <- rnorm( n )
  mean( sample ) / sd( sample )
} ) -> many_estimates

# Plot histogram
hist( many_estimates, breaks=300, freq=FALSE, 
  xlim=c(-3,3), ylim=c(0,.9) )

# Normalverteilung, wie zuvor:
xg <- seq( -2, 2, length.out=1000 )
lines( x = xg, y = dnorm( xg*sqrt(n) )*sqrt(n), col="magenta" )

# Studentsche t-Verteilung
lines( x = xg, y = dt( xg*sqrt(n), n-1 )*sqrt(n), col="blue" )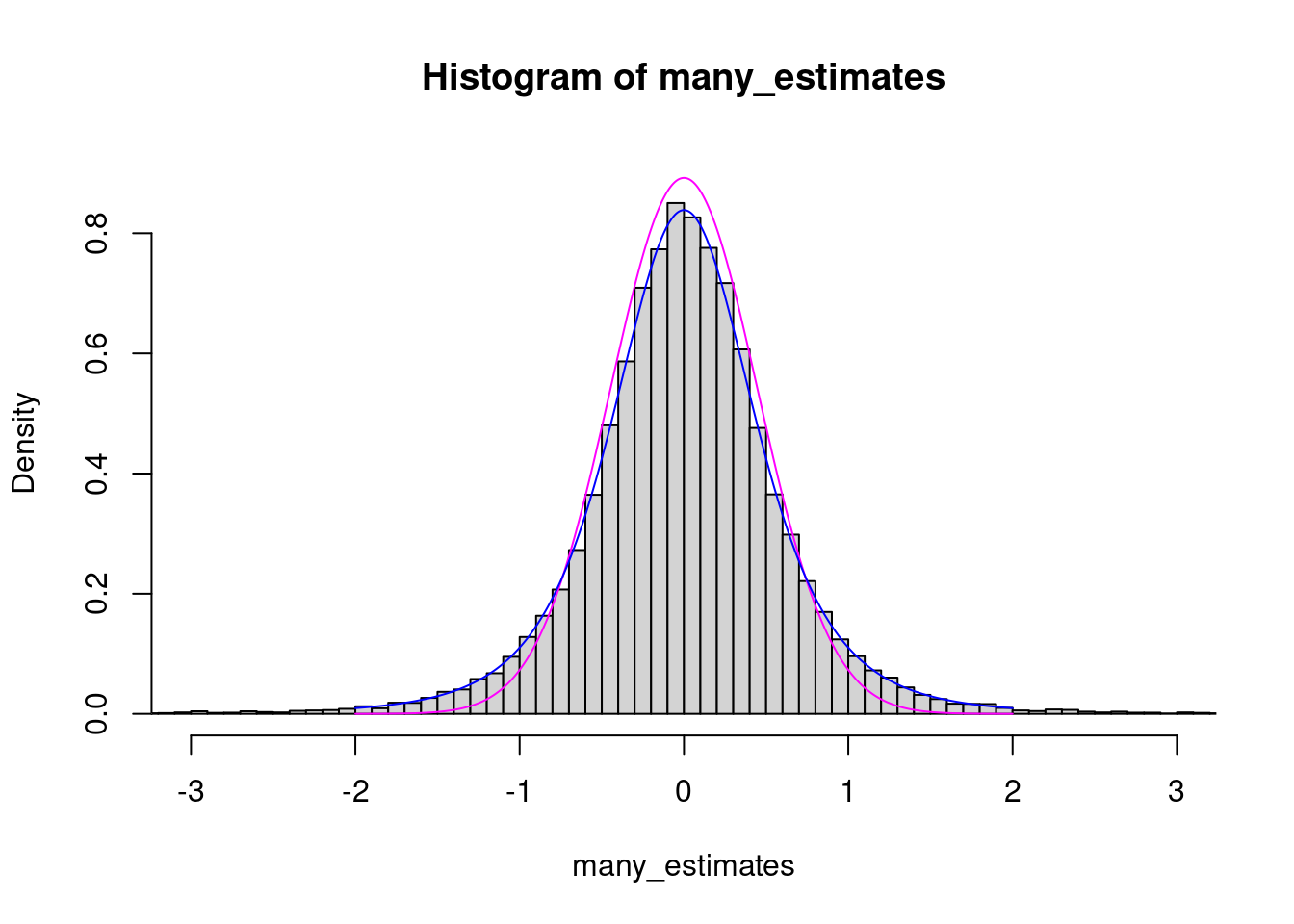

Wir haben hier dt für die blaue und dnorm für die magenta-Kurve verwendet. Die Formel hinter dnorm ist die der Standard-Normalverteilung (siehe vorige Vorlesung), die hinter dt ist die für die Student-Verteilung für \(n-1\) Freiheitsgrade (die Sie nachschlagen können, wenn es Sie interessiert).

Oben haben wir berechnet, dass wir den Standardfehler mit 1.96 multiplizieren müssen, um ein 95%-Konfidenzintervall für einen Mittelwert zu erhalten. Auf die 1.96 sind wir gekommen vie die 2.5%- und 97.5%-Quantile der Standardnormalverteilung:

qnorm( 0.025 )

[1] -1.959964

qnorm( 0.975 )

[1] 1.959964

Dann haben wir festgestellt, dass die nicht mehr passt, wenn der Stichproben-Umfang \(n\) klein ist. Hier können wir nun die Quantile der t-Verteilung mit \(n-1\) Freiheitsgraden (degrees of freedom, d.f.) verwenden:

n <- 5
qt( 0.025, df=n-1 )

[1] -2.776445

qt( 0.975, df=n-1 )

[1] 2.776445

Wir sehen, dass wir das Interval deutlich breiter machen müssen.

Für großes \(n\) erhalten wir hingegen fast dieselben Werte wie zuvor:

n <- 100
qt( 0.025, df=n-1 )

[1] -1.984217

qt( 0.975, df=n-1 )

[1] 1.984217

Konfidenzintervalle für Mittelwerte mit Students Korrektur

Zur Erinnerung: Weiter oben haben wir folgendes versucht:

Wir haben angenommen, dass die Körpergrößen der Männer in Deutschland normalverteilt sind mit Erwartungswert 178 cm, und Standardabweichung 7 cm. Dann haben wir sehr oft folgende Simulation wiederholt: Wir ziehen eine Stichprobe aus \(n\) Männern, bestimmen Mittelwert und Standardabweichung der Körpergrößen in der STichprobe und konstruieren daraus ein 95%-Konfidenzintervall, indem wir Mittelwert plus/mins 1.96 * Standardabweichung rechnen. Dann haben wir ermittelt, wie oft das Konfidenzintervall den wahren Wert enthält.

Nochmal, wie schon oben:

n <- 100
replicate( 3000, {
   height_sample <- rnorm( n, mean=178, sd=7 )   # <- hier 10 statt 100
   sample_mean <- mean( height_sample )
   sem <- sd( height_sample ) / sqrt(100)
   c( lower = sample_mean - 1.96*sem, upper = sample_mean + 1.96*sem )
}) %>% 
t %>% as_tibble() %>%
mutate( contains_true_value = lower < 178 & upper > 178 ) %>%
summarise( mean( contains_true_value ) )

# A tibble: 1 × 1
  `mean(contains_true_value)`
                        <dbl>
1                       0.952

Mit \(n=100\) funktioniert das gut, mit \(n=8\) aber nicht mehr sonderlich:

n <- 8
replicate( 3000, {
   height_sample <- rnorm( n, mean=178, sd=7 )   # <- hier 10 statt 100
   sample_mean <- mean( height_sample )
   sem <- sd( height_sample ) / sqrt(n)
   c( lower = sample_mean - 1.96*sem, upper = sample_mean + 1.96*sem )
}) %>% 
t %>% as_tibble() %>%
mutate( contains_true_value = lower < 178 & upper > 178 ) %>%
summarise( mean( contains_true_value ) )

# A tibble: 1 × 1
  `mean(contains_true_value)`
                        <dbl>
1                       0.914

Wie wir eben gesehen haben, müssen wir den Faktor 1.96 mit qt statt qnorm berechnen. Für \(n=10\) erhalten wir dann:

qt( .975, n-1 )

[1] 2.364624

Mit diesem Faktor klappt es nun:

n <- 8
replicate( 3000, {
   height_sample <- rnorm( n, mean=178, sd=7 )   # <- hier 10 statt 100
   sample_mean <- mean( height_sample )
   sem <- sd( height_sample ) / sqrt(n)
   c( lower = sample_mean - 2.26*sem, upper = sample_mean + 2.26*sem )
}) %>% 
t %>% as_tibble() %>%
mutate( contains_true_value = lower < 178 & upper > 178 ) %>%
summarise( mean( contains_true_value ) )

# A tibble: 1 × 1
  `mean(contains_true_value)`
                        <dbl>
1                       0.931

Zusammenfassung

Hier wird gezeigt, wie man Konfidenzintervalle für Mittelwerte berechnet.

Fassen wir zusammen:

Wir haben eine Stichprobe mit \(n\) Werten, z.B.

n <- 12

mysample <- runif( n, min=0, max=10 )   # wahrer Mittelwert: 5
mysample

 [1] 2.4653795 6.6977660 8.3400690 2.2811362 2.2907615 2.8882489 2.5625476
 [8] 5.4466987 5.4032498 2.7041405 0.7649689 7.6660676

Wir bestimmen den Mittelwert der Stichprobe:

sample_mean <- mean( mysample )
sample_mean

[1] 4.12592

Nun berechnen wir den Standardfehler des Mittelwerts (SEM) mit der üblichen Formel

sem <- sd( mysample ) / sqrt(n)
sem

[1] 0.712996

Nun möchten wir ein \((1-\alpha)\)-Konfidenzintervall zu diesem Mittelwert konstruieren. (Für ein 95%-Konfidenzintervall z.B. ist \(\alpha=0,\!05\).) Wir bestimmen den Faktor mittelts qt:

alpha <- 1 - 0.95  # 0.05
f <- -qt( alpha/2, n-1 )
f

[1] 2.200985

Nun multiplizieren wir den SEM mit dem errechneten Faktor und bauen das KOnfidenzintervall:

c( sample_mean - f*sem, sample_mean + f*sem )

[1] 2.556626 5.695213

Wir berichten also: Aus unserer Stichprobe haben wir einen Mittelwert von 4.13 ermittelt mit einem 95%-KI von (2.56;2.56). In Papers wird das oft kurz geschrieben als: “4.13 (95%-CI: 2.56-2.56).

Noch einfacher

Die t-Test-Funktion verwendet, wie der Name schon sagt, die t-Verteilung, und kann daher das 95%-KI berechnen, wenn wir ihr unsere Einzeldaten geben

t.test( mysample )

    One Sample t-test

data:  mysample
t = 5.7867, df = 11, p-value = 0.0001216
alternative hypothesis: true mean is not equal to 0
95 percent confidence interval:
 2.556626 5.695213
sample estimates:
mean of x 
  4.12592 

Hier können wir das 95%-KI direkt ablesen. Intern hat t.test die Rechnung von eben durchgeführt.

Den p-Wert sollten wir hier aber ignorieren, denn wir haben die Funktion ja nur benutzt, um das KI zu berechnen, und haben gar keine Hypothese, die wir testen können.

Also: Einfachste Methode, um einen Mittelwert mit seinem 95%-KI zu gegebenen Daten zu berechnen: Man übergebe den Daten-Vektor an die Funktion t.test.

Wenn das Konfidenzlevel nicht 95%, sondern z.B. 99% betragen soll, teilt man das der t.test-Funktion einfach mit:

t.test( mysample, conf.level=0.99 )

    One Sample t-test

data:  mysample
t = 5.7867, df = 11, p-value = 0.0001216
alternative hypothesis: true mean is not equal to 0
99 percent confidence interval:
 1.911492 6.340347
sample estimates:
mean of x 
  4.12592 

Wenn Sie auf die einzelnen Daten der Ausgabe zugreifen möchten, geht da so:

res = t.test( mysample )

# Mittelwert:
res$estimate

mean of x 
  4.12592 

cat( "-----\n" )   # Print spacer

-----

# Konfidenzinterval
res$conf.int

[1] 2.556626 5.695213
attr(,"conf.level")
[1] 0.95

Hausaufgabe

Simulieren Sie nochmals die Situation mit der Zwiebel-Aufgabe vom letzten Mal, wo wir die Ernte von zwei Versuchsfeldern vergleichen, wo ein Dünger für den Anbau von Zwiebeln erprobt wird.

• Das Gewicht der Zwiebeln, die auf dem Feld wachsen, das mit dem neuen Dünger gedüngt wurde (“treated field”), folgt einer Normalverteilung mit Erwartungswert 88 g und Standardabweichung 9 g. Simulieren Sie die Ernte von 10 Zwiebeln, indem Sie mit rnorm 10 Zahlen aus der genannten Verteilung ziehen.

• Das Gewicht der Zwiebeln auf dem konventionell behandelten Vergleichsfeld (“control field”) folgt einer Normalverteilung mit Erwartungswert 80 g und Standardabweichung 9 g. Simulieren Sie auch hier die Ernte von 10 Zwiebeln, indem Sie mit rnorm 10 Zahlen aus der genannten Verteilung ziehen.

• Berechnen Sie für die beiden Stichproben von je 10 Zwiebeln Mittelwert und zugehöriges 95%-Konfidenzintervall.

• Liegt die Untergrenze des KI des behandelten Feldes über der Obergrenze des KI des Vergleichsfeldes?

• Was sagt uns die Antwort auf die o.g. Frage, wenn wir das Experiment bewerten?

• Führen Sie die o.g. Schritte 20 mal durch und zählen Sie, wie oft die KIs überlappen und wie oft nicht.

• Nehmen Sie nun an, der Dünnger habe keinen Einfluss, der Gewichts-Verteilung im behandelten Feld sei dieselbe wie im Vergleichfeld (Erwartungswert bei beiden 80 g). Wiederholen Sie die Aufgabe für dieses Setting. Wie oft überlappen die KIs nun?

• Für Fortgeschrittene: Den Code 20 mal auszuführen und jeweils per Auge zu schauen ob die KIs sich überlappen, ist mühsam. Gelingt es Ihnen, dies mit replicate so zu automatisieren, dass Sie die Simulation mühelos auch 1000 mal statt nur 20 mal durchzuführen?

Als Ausblick: Wenn wir die Frage stellen, ob sich die KIs überlassen, machen wir fast schon das, was der t-Test macht. Zwei Kleinigkeiten sind aber anders, so dass unser Verfahren nur fast dasselbe Ergebnis bringt als ein t-Test. Dieses Detail besprechen wir das nächste Mal.