suppressPackageStartupMessages( library(tidyverse) )Binomialverteilung und Binomialtest
Vorlesung “Datenanalyse in der Biologie”
Einführendes Beispiel: Ein gezinkter Würfel
Sie haben einen Würfel, bei dem Sie vermuten, dass er manipuliert wurde, so dass die Sechs häugiger erscheint als in 1/6 der Würfe. Sie werfen den Würfel 600 mal und erhalten 130 mal die Sechs, also 30% öfter als die erwartetem 100 mal. Wie beurteilen wir dieses Ergebnis?
Simulation von Würfen: Bernoulli-Versuche und die Binomial-Verteilung
Wir stellen folgende Nullhypothese auf: “Der Würfel ist nicht manipuliert; die Wahrscheinlichkeit, eine Sechs zu werfen, ist also 1/6.”
Um den Wurf einen solchen normalen Würfels zu simulieren, bietet uns R eine Reihe von Möglichkeiten, von denen wir nun eine verwenden.
Benoulli-Versuche
Als Bernoulli-Versuch (Bernoulli trial) bezeichnet man ein Zufallsexperiment, bei dem es genau zwei mögliche Ausgänge gibt, z.B. Kopf oder Zahl beim Münzwurf, Sechs oder Nicht-Sechs bei unserem Würfel, oder z.B. Treffer oder kein Treffer, wenn das Experiment ist, in einer Jahrmarkt-Schießbude ein Ziel zu treffen.
Bei Bernoulli-Experimenten bezeichnet man eines der beiden möglichen Ergebnisse als “Erfolg” (success) und das andere als Fehlschlag (failure). Zum Beispiel könnte man beim Münzwurd Kopf als Erfolg und Zahl als Fehlschlag ansehen, beim Würfel Sechs als Erfolg und alle anderen als Fehlschlag, und beim Jahrmarkt-Schießen ist natürlich der Treffer der Erfolg.
Für die Erfolgs-Wahrscheinlichkeit (success probability) hat man häufig eine Vermutung oder Null-Hypothese: 1/2 bei der Münze, 1/6 beim Würfel. Beim Jahrmarkt-Schießen variiert hingegen die Erfolgs-Wahrscheinlichkeit sicher von Schütze zu Schütze (und von Gewehr zu Gewehr).
Simulation eines Bernoulli-Versuchs
Mit runif können wir eine im Interval 0 bis 1 gleichverteilte Zufallszahl (uniformly distributed random number) ziehen:
runif(1) # 1 ist die Anzahl der zu ziehenden Zahlen[1] 0.7274755Da aus einer Gleichverteilung von 0 bis 1 gezogen wird, ist die Zahl mit Wahrscheinlichkeit 1/6 kleiner als 1/6 ist. Wenn mir also 600 Zahlen ziehen, werden ungefähr 100 davon kleiner als 1/6 sein
runif(100) < 1/6 [1] TRUE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE TRUE
[13] FALSE TRUE TRUE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
[25] FALSE FALSE FALSE FALSE FALSE FALSE TRUE FALSE FALSE FALSE FALSE TRUE
[37] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
[49] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE TRUE FALSE FALSE FALSE
[61] FALSE FALSE TRUE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
[73] TRUE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
[85] FALSE FALSE TRUE FALSE FALSE FALSE FALSE FALSE FALSE FALSE TRUE FALSE
[97] TRUE FALSE TRUE TRUEMit sum können wir die Anzahl der TRUEs unter den 600 Werten ermitteln:
sum( runif(600) < 1/6 )[1] 104Wenn wir dies mehrmals durhführen, erhalten wir natürlich jedes mal leicht unterschiedliche Werte
sum( runif(600) < 1/6 )[1] 107sum( runif(600) < 1/6 )[1] 104sum( runif(600) < 1/6 )[1] 89sum( runif(600) < 1/6 )[1] 98Die Binomialverteilung aus Simulation
Wenn wir den Code von eben sehr oft durchführen, sehen wir, wie häufig jeder Wert ist:
set.seed( 13245768 )
replicate( 10000, {
sum( runif(600) < 1/6 )
} ) -> many_tries
head( many_tries )[1] 80 120 110 105 91 104Jede einzelne dieser Zahlen ist die Simulation des folgenden Versuchs: Ein Würfel wird 600 mal geworfen, dann wird gezählt, wie oft eine Sechs geworfen wurde.
Wir erwarten natürlich, dass diese Anzahl über sehr viele Versuche sich zu einem Wert von 600/6=100 mittelt. Man sagt: Der Erwartungswert (expectation value) der Versuchs-Statistik “Anzahl der Sechsen” ist 100.
Was ist der Mittelwert über unsere 10000 Versuche?
mean( many_tries )[1] 100.1147Was aber ist die Verteilung (distribution)? Wie häufig komt jeder mögliche Wert jeweils vor?
Wir zählen durch:
tibble( numSix = many_tries ) %>%
group_by( numSix ) %>%
summarise( n = n() ) -> distr
distr# A tibble: 69 × 2
numSix n
<int> <int>
1 66 1
2 67 2
3 68 1
4 69 2
5 72 2
6 73 6
7 74 9
8 75 7
9 76 13
10 77 14
# ℹ 59 more rowsund erstellen einen Plot
distr %>%
ggplot +
geom_col( aes( x=numSix, y=n ))
Natürlich können wir die y-Ache auch mit Anteilen (proprtions) ebschriften, indem wir durch 10000 (die Anzahl der Versuche) teilen:
distr %>%
ggplot +
geom_col( aes( x=numSix, y=n/sum(n) )) +
xlab("number of sixes in 100 dice throws") + ylab("frequency")
Nun können wir für jeden Wert \(k\) ablesen, wie häufig es vorgekommen ist, dass bei \(n=600\) Würfen genau \(k\) mal die Sechs gewürfelt wurde.
Zurück zum gezinkten Würfel
Wie häufig ist es vorgekommen, dass unser normaler Würfel 130 mal oder noch öfter eine Sechs gezeigt hat?
sum( many_tries >= 130 )[1] 13Das war nur in 13 der 10000 Versuche der Fall.
Wir hätten übrigens auch die distr-Tabelle verwenden können:
distr %>%
filter( numSix >= 130 ) %>%
summarise( sum(n) )# A tibble: 1 × 1
`sum(n)`
<int>
1 13In jedem Fall ist es nur in 13/1000=0.13% der Versuche vorgekommen, dass 130 oder mehr Sechsen geworfen wurden.
Bei dem “verdächtigen” Würfel aus dem Beispiel ganz am Anfang haben wir einen Versuch gemacht, in dem wir den Würfel 600 mal geworfen haben, und dabei 130 mal eine Sechs erhalten.
Die Wahrscheinlichkeit, dass so etwas mit einem fairen Würfel geschieht, ist, wie wir gerade gesehen haben, nur etwa 0.13%. Das ist nicht unmöglich, aber sehr unwahrscheinlich.
Wir können also die Nullhypothese, dass der verdächtige Würfel ganz normal und nicht manipuliert war, mit einem p-Wert von 0,13% ablehnen und sagen: Dieser Würfel ist gezinkt.
Der Zentraler Grenzwertsatz zeigt sich wieder
Sehen Sie sich noch mal das Histogramm von oben an. Warum wirkt es so glockenförmig (normalverteilt)?
Der Wert \(K\), dessen Verteilung dargestellt ist, also die Anzahl der Sechsen in 600 Würfen, kann als Summe von vielen unabhqngigen Zufallszahlen dargestellt werden: \(K\) ist die Summe aus 600 Zufallswerten, die jeweils entweder 0 (keine Sechs) oder 1 (Sechs) ist. Folglich gilt der zentrale Grenzwertsatz und \(K\) ist näherungsweise normalverteilt. Zusätzlich zu dieser Nqherung gibt es auch eine exakte Formel, die wir gleich kennen lernen.
Binomialverteilung: Definition und Verteilungsfunktion
Definition: Ein Bernoulli-Versuch mit Erfolgswahrscheinlichkeit \(p\) werde \(n\) mal wiederholt. Dabei werde gezählt, wie viele der \(n\) Versuche erfolgreich waren; diese Zahl werde mit \(K\) bezeichnet. Dann sagt nennt man die Verteilung der Zufallsvariablen \(K\) die Binomialverteilung für \(n\) Versuche mit Erfolgswahrscheinlickeit \(p\) (binomial distribution for \(n\) trials with success probability \(p\)).
Also: Die Anzahl \(K\) der Sechsen, die man erhält, wenn man einen Würfel 600 mal wirft, ist binomialverteilt mit \(n=600\) und \(p=1/6\). Man schreibt: \(K \sim \text{Binom}(n\!=\!600,\,p\!=\!1/6)\)
Herleitung der Binomialverteilung
(nur für Interessierte)
Wie groß ist die Wahrscheinlichkeit, bei z.B. \(n=10\) Würfen genau \(k=2\) mal eine Sechs zu erhalten? Wir schreiben E (Erfolg) für eine Sechs und F (Fehlschlag) für eine Nicht-Sechs. Dann beschreibt die Zeichenkette FFFEFFFFEF einen Möglichen Ausgang des Versuchs, nämlich, dass man zweimal eine Sechs gewürfelt hat, nämlich beim 4. und 8. Wurf. Die Wahrscheinlichkeit für genau dieses Ergebnis ist \(\left(\frac{1}{6}\right)^2\left(\frac{5}{6}\right)^8\), da die zwei Erfolge jeweils die Wahrscheinlichkeit 1/6 haben und die 8 Fehlschläge jeweils 5/8. Es gibt aber \(\left( 10\atop 2\right) = 10\cdot 9/2\) Möglichkeiten, die zwei E auf die 10 Würfe zu verteilen. Also ist die Wahrscheinlichkeit, 2 Sechsen in 10 Würfen zu werfen: \(10\cdot 9/2 \cdot \left(\frac{1}{6}\right)^2\left(\frac{5}{6}\right)^8=0.29\).
Allgemein schreiben wir also
\[\text{Prob}_\text{binom}(k;n,p) = \left( n \atop k \right) p^n (1-p)^{n-k}.\] Der Binomialkoeffizient \(\left(n \atop k\right)\) in der Formel gibt der Verteilung ihren Namen.
In R können wir die Formel so schreiben:
n <- 10
p <- 1/6
k <- 2
choose( n, k ) * p^k * (1-p)^(n-k)[1] 0.29071Die Binomialverteilung in R
Diese Formel müssen wir natürlich nicht jedesmal tippen. Sie ist in R fest eingebaut, als die Funktion dbinom:
dbinom( k, n, p )[1] 0.29071Damit können wir nun exakt ausrechnen, wie wahrscheinlich es ist, \(k\) Sechsen zu erhalten, wenn man einen Würfel \(n\) mal wirft:
tibble( numSix = 0:600 ) %>%
mutate( prob = dbinom( numSix, 600, 1/6 ) )# A tibble: 601 × 2
numSix prob
<int> <dbl>
1 0 3.10e-48
2 1 3.72e-46
3 2 2.23e-44
4 3 8.88e-43
5 4 2.65e-41
6 5 6.32e-40
7 6 1.25e-38
8 7 2.13e-37
9 8 3.15e-36
10 9 4.15e-35
# ℹ 591 more rowsWir plotten das als Säulendiagramm:
tibble( numSix = 0:600 ) %>%
mutate( prob = dbinom( numSix, 600, 1/6 ) ) %>%
ggplot +
geom_col( aes( x=numSix, y=prob ) )
Vielleicht soltlen wir uns auf die Werte \(k\) beschränken, wo die Wahrscheinlichkeit nicht winzig ist
tibble( numSix = 60:150 ) %>%
mutate( prob = dbinom( numSix, 600, 1/6 ) ) %>%
ggplot +
geom_col( aes( x=numSix, y=prob ) )
Dies ist dasselbe Histogramm wie weiter oben. Nun sehen wir aber, wie es auussähe, wenn wir nicht 10000 Versuche, sondern unendlich viele machen könnten.
Damit können wir nun auch unsere ursprüngliche Frage beantworten: Wie wahrscheinlich ist es, dass man mit mindestens 130 mal eine Sechs wirft, wenn man 600 mal würfelt. Dazu berechnen wir für alle Zahlen von k=130$ bis \(k=600\), wie wahrschenlich es ist, genau \(k\) Sechsen zu erhalten:
dbinom( 130:600, 600, 1/6 ) [1] 2.593839e-04 1.861228e-04 1.322600e-04 9.307921e-05 6.487760e-05
[6] 4.478957e-05 3.062816e-05 2.074667e-05 1.392132e-05 9.254169e-06
[11] 6.094531e-06 3.976574e-06 2.570771e-06 1.646732e-06 1.045217e-06
[16] 6.574055e-07 4.097528e-07 2.530990e-07 1.549376e-07 9.400242e-08
[21] 5.652679e-08 3.369146e-08 1.990456e-08 1.165653e-08 6.766842e-09
[26] 3.894208e-09 2.221696e-09 1.256602e-09 7.046517e-10 3.917686e-10
[31] 2.159625e-10 1.180416e-10 6.397563e-11 3.438199e-11 1.832309e-11
[36] 9.683474e-12 5.075074e-12 2.637823e-12 1.359735e-12 6.951544e-13
[41] 3.524842e-13 1.772727e-13 8.843024e-14 4.375508e-14 2.147519e-14
[46] 1.045535e-14 5.049459e-15 2.419176e-15 1.149788e-15 5.421347e-16
[51] 2.535986e-16 1.176922e-16 5.419013e-17 2.475571e-17 1.122079e-17
[56] 5.046324e-18 2.251854e-18 9.970778e-19 4.380778e-19 1.909927e-19
[61] 8.262945e-20 3.547442e-20 1.511358e-20 6.389992e-21 2.681161e-21
[66] 1.116463e-21 4.613955e-22 1.892424e-22 7.703504e-23 3.112370e-23
[71] 1.248061e-23 4.967405e-24 1.962371e-24 7.694814e-25 2.994942e-25
[76] 1.157070e-25 4.437309e-26 1.689178e-26 6.383145e-27 2.394443e-27
[81] 8.916450e-28 3.296128e-28 1.209617e-28 4.406867e-29 1.593886e-29
[86] 5.723162e-30 2.040201e-30 7.220620e-31 2.537154e-31 8.851074e-32
[91] 3.065690e-32 1.054265e-32 3.599696e-33 1.220345e-33 4.107770e-34
[96] 1.372908e-34 4.556110e-35 1.501309e-35 4.912176e-36 1.595921e-36
[101] 5.148580e-37 1.649329e-37 5.246571e-38 1.657286e-38 5.198496e-39
[106] 1.619276e-39 5.008778e-40 1.538561e-40 4.693258e-41 1.421723e-41
[111] 4.277018e-42 1.277781e-42 3.791103e-43 1.117049e-43 3.268743e-44
[116] 9.499367e-45 2.741687e-45 7.858763e-46 2.237212e-46 6.325291e-47
[121] 1.776142e-47 4.953384e-48 1.372009e-48 3.774379e-49 1.031267e-49
[126] 2.798577e-50 7.543039e-51 2.019304e-51 5.369157e-52 1.417955e-52
[131] 3.719405e-53 9.690403e-54 2.507669e-54 6.445568e-55 1.645573e-55
[136] 4.172925e-56 1.051075e-56 2.629656e-57 6.534891e-58 1.613074e-58
[141] 3.955017e-59 9.632146e-60 2.330129e-60 5.599139e-61 1.336437e-61
[146] 3.168570e-62 7.462212e-63 1.745673e-63 4.056491e-64 9.363370e-65
[151] 2.146887e-65 4.889707e-66 1.106253e-66 2.486137e-67 5.550039e-68
[156] 1.230745e-68 2.711083e-69 5.932264e-70 1.289444e-70 2.784127e-71
[161] 5.971473e-72 1.272273e-72 2.692687e-73 5.661075e-74 1.182279e-74
[166] 2.452728e-75 5.054608e-76 1.034748e-76 2.104219e-77 4.250663e-78
[171] 8.529665e-79 1.700265e-79 3.366751e-80 6.622387e-81 1.293980e-81
[176] 2.511593e-82 4.842614e-83 9.275105e-84 1.764679e-84 3.335186e-85
[181] 6.261543e-86 1.167748e-86 2.163327e-87 3.981075e-88 7.277507e-89
[186] 1.321503e-89 2.383724e-90 4.271151e-91 7.602112e-92 1.344072e-92
[191] 2.360527e-93 4.118054e-94 7.136255e-95 1.228408e-95 2.100426e-96
[196] 3.567493e-97 6.018776e-98 1.008651e-98 1.679035e-99 2.776277e-100
[201] 4.559825e-101 7.438989e-102 1.205475e-102 1.940344e-103 3.102226e-104
[206] 4.926520e-105 7.770999e-106 1.217533e-106 1.894741e-107 2.928745e-108
[211] 4.496484e-109 6.856809e-110 1.038546e-110 1.562361e-111 2.334458e-112
[216] 3.464470e-113 5.106589e-114 7.475929e-115 1.087017e-115 1.569790e-116
[221] 2.251527e-117 3.207304e-118 4.537606e-119 6.375786e-120 8.897284e-121
[226] 1.233088e-121 1.697228e-122 2.320021e-123 3.149525e-124 4.246157e-125
[231] 5.685132e-126 7.559178e-127 9.981457e-128 1.308863e-128 1.704399e-129
[236] 2.204044e-130 2.830330e-131 3.609250e-132 4.570408e-133 5.747072e-134
[241] 7.176073e-135 8.897557e-136 1.095452e-136 1.339212e-137 1.625674e-138
[246] 1.959480e-139 2.345122e-140 2.786776e-141 3.288101e-142 3.852023e-143
[251] 4.480511e-144 5.174344e-145 5.932886e-146 6.753886e-147 7.633299e-148
[256] 8.565156e-149 9.541495e-150 1.055235e-150 1.158583e-151 1.262826e-152
[261] 1.366442e-153 1.467789e-154 1.565143e-155 1.656741e-156 1.740840e-157
[266] 1.815762e-158 1.879956e-159 1.932045e-160 1.970880e-161 1.995578e-162
[271] 2.005556e-163 2.000555e-164 1.980649e-165 1.946245e-166 1.898071e-167
[276] 1.837145e-168 1.764745e-169 1.682362e-170 1.591646e-171 1.494357e-172
[281] 1.392304e-173 1.287288e-174 1.181055e-175 1.075247e-176 9.713580e-178
[286] 8.707113e-179 7.744307e-180 6.834305e-181 5.984104e-182 5.198601e-183
[291] 4.480699e-184 3.831477e-185 3.250400e-186 2.735561e-187 2.283935e-188
[296] 1.891636e-189 1.554161e-190 1.266623e-191 1.023952e-192 8.210712e-194
[301] 6.530380e-195 5.151576e-196 4.030631e-197 3.127695e-198 2.407028e-199
[306] 1.837088e-200 1.390457e-201 1.043638e-202 7.767716e-204 5.732893e-205
[311] 4.195435e-206 3.044307e-207 2.190248e-208 1.562344e-209 1.104901e-210
[316] 7.746721e-212 5.384492e-213 3.710120e-214 2.534144e-215 1.715768e-216
[321] 1.151471e-217 7.659453e-219 5.049816e-220 3.299659e-221 2.136784e-222
[326] 1.371298e-223 8.720977e-225 5.495933e-226 3.431958e-227 2.123477e-228
[331] 1.301784e-229 7.906714e-231 4.757720e-232 2.836135e-233 1.674787e-234
[336] 9.796602e-236 5.676143e-237 3.257401e-238 1.851429e-239 1.042169e-240
[341] 5.809537e-242 3.206963e-243 1.752959e-244 9.487472e-246 5.084004e-247
[346] 2.697198e-248 1.416596e-249 7.365109e-251 3.790412e-252 1.930815e-253
[351] 9.734526e-255 4.857144e-256 2.398341e-257 1.171860e-258 5.665605e-260
[356] 2.710145e-261 1.282579e-262 6.004682e-264 2.780857e-265 1.273848e-266
[361] 5.771313e-268 2.585925e-269 1.145796e-270 5.020120e-272 2.174708e-273
[366] 9.313900e-275 3.943385e-276 1.650350e-277 6.826750e-279 2.790896e-280
[371] 1.127522e-281 4.501085e-283 1.775328e-284 6.917781e-286 2.662797e-287
[376] 1.012390e-288 3.801464e-290 1.409616e-291 5.161193e-293 1.865736e-294
[381] 6.658115e-296 2.345324e-297 8.153667e-299 2.797359e-300 9.469660e-302
[386] 3.162683e-303 1.041969e-304 3.385896e-306 1.085055e-307 3.428691e-309
[391] 1.068169e-310 3.280366e-312 9.929077e-314 2.961637e-315 8.704047e-317
[396] 2.520031e-318 7.186185e-320 2.015788e-321 5.434722e-323 0.000000e+00
[401] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
[406] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
[411] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
[416] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
[421] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
[426] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
[431] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
[436] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
[441] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
[446] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
[451] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
[456] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
[461] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
[466] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
[471] 0.000000e+00Wir addieren alle diese Werte:
sum( dbinom( 130:600, 600, 1/6 ) )[1] 0.0008721039Dies ist nun der exakte p-Wert, mit dem wir unsere Nullhypothese “Der Würfel ist nicht gezinkt” verwerfen. (Der Wert, den wir zuvor erhalten hatten, war ungenau, da wir ja nicht unendlich viele, sondern nur 10000 Versuche gemacht hatten).
Wir können die Rechnung von eben auch schreiben, indem wir berechnen, wie wahrscheinlich es ist, höchstens 129 Sechsen zu werfen
sum( dbinom( 0:129, 600, 1/6 ) )[1] 0.9991279und das von 1 abziehen:
1 - sum( dbinom( 0:129, 600, 1/6 ) )[1] 0.0008721039Wir erhalten denselben Wert.
Für die Frage “Wie wahrscheinlich ist es, höchstens \(k\) Sechsen zu erzielen?” gibt es in R eine Abkürzung für die Summe:
Statt
sum( dbinom( 0:129, 600, 1/6 ) )[1] 0.9991279kann man auch schreiben
pbinom( 129, 600, 1/6 ) [1] 0.9991279Allgemein: Die R-Funktionen für Verteilungen, die mit d beginnen (dbinom, dnorm etc.) berechnen die Wahrscheinlichkeit(sdichte) für einen Wert; die, die mit p beginnen (pbinom, pnorm) die Gesamtwahrscheinlichkeit für alle Werte, die kleienr oder gleich dem gegebenen Wert sind; sie stellen also die Summe (oder das Integral) aller d-Werte bis zum angegeben Wert dar.
Der Binomialtest
Die Methode, wie wir eben einen p-Wert erhalten haben, nennt man einen Binomialtest. Parallel zur FUnktion t.test für t-Tests gibt es auch eine Funktion binomial.test für Binomial-Tests, die im Wesentlichen genau die Rechnung durchführt, die wir eben per Hand gemacht haben:
Die Funktion benutzt man wie folgt:
binom.test( 130, 600, 1/6, alternative="greater" )
Exact binomial test
data: 130 and 600
number of successes = 130, number of trials = 600, p-value = 0.0008721
alternative hypothesis: true probability of success is greater than 0.1666667
95 percent confidence interval:
0.1892486 1.0000000
sample estimates:
probability of success
0.2166667 Wir haben der binom.test Funktion als Argumente übergeben: Die Anzahl der Erfolge (130 Sechsen), die Anzahl der Versuche (600 Würfe) und die in der Nullhypothese angenommene Erolgswahrscheinlichkeit (1/6 für einen nicht gezinkten Würfel).
Dann hat uns binom.test die Wahrscheinlichkeit berechnet, dass man das beobachtete Ergebnis (130 Sechsen) oder ein noch extremeres (mehr als 130 Sechsen) erhält, wenn die Nullhypothese (Wahrscheinlichkeit für eine Sech ist 1/6) zutrifft, und diese Wahrscheinlichkeit als p-Wert ausgegeben.
Ein- und zweiseitige Tests
Was bedeutet im vorigen Absatz “oder ein noch extremeres Ergebnis”? Wenn wir viel weniger Sechsen erhieltem als erwartet, z.B. nur 50 statt der erwarteten 100, wäre das nicht auch ein Grund, die Nullhypothese abzulehnen?
Bisher sind wir implizit davon ausgegangen, dass der Falschspieler den Würfel zu seinem Vorteil manipuliert hat, also die Sechs mit Zink beschwert hat. Die Möglichkeit, dass der Würfel “in die andere Richtung” manipuliert wurde, haben wir außer acht gelassen.
Wir haben der binom.test-Funktion diese Annahme mitgeteilt, indem wir durch die Angabe alternative="greater" vorgegeben werden soll, dass nur die Alternativ-Hypothese “Die tatsächliche Wahrscheinlichkeit ist größer als 1/6” berücksichtig werden soll.
Die umfassendere Alternative zur Nullhypothese wäre “Die Wahrscheinlichkeit ist kleiner oder größer, also einfacher: ist ungleich 1/6.”
Wenn wir binom.test nicht anderweitig anweisen, verwendet es diese sog. “zweiseitige” Alternative:
binom.test( 130, 600, 1/6 ) # Verwende Default-Wert alternative="two.sided" )
Exact binomial test
data: 130 and 600
number of successes = 130, number of trials = 600, p-value = 0.001457
alternative hypothesis: true probability of success is not equal to 0.1666667
95 percent confidence interval:
0.1843313 0.2518190
sample estimates:
probability of success
0.2166667 Der p-Wert ist nun ein wenig höher als zuvor.
Der zweiseitige Test liefert stets einen höheren p-Wert als der einseitige Test. Man sagt, er sei konservativer (more conservative). Damit ist gemeint, dass seine Verwendung die Wahrscheinlichkeit einer falsch-positiven Schlussfolgerung verringert, und man ihn daher vorzieht, wenn man nicht ganz sicher ist, dass die Verwendung eines einseitigen Tests gerechtfertigt ist.
Berechnung des zweiseitigen p-Werts
(nur für Interessierte)
(oder eigentlich: nur als Notiz für mich selbst; da ich es gerade selbst nachschlagen musste; Sie können diesen Einschub ignorieren)
Die Formulierung “so extrem wie 160 Sechsen, oder noch extremer” wird beim einseitigen Test interpretiert als “160 Secseh oder mehr”, beim zweiseitigemn Test jedoch wie folgt:
Wir berechnen die Wahrscheinlichkeit für jede mögliche Anzahl \(k\) an Sechsen und markieren, welche Anzahlen genauso oder noch unwahrscheinlicher ist als die Anzahl 130:
tibble( numSix = 0:600 ) %>%
mutate( prob = dbinom( numSix, 600, 1/6 ) ) %>%
mutate( as_or_even_less_likely = prob <= dbinom( 130, 600, 1/6 ) )# A tibble: 601 × 3
numSix prob as_or_even_less_likely
<int> <dbl> <lgl>
1 0 3.10e-48 TRUE
2 1 3.72e-46 TRUE
3 2 2.23e-44 TRUE
4 3 8.88e-43 TRUE
5 4 2.65e-41 TRUE
6 5 6.32e-40 TRUE
7 6 1.25e-38 TRUE
8 7 2.13e-37 TRUE
9 8 3.15e-36 TRUE
10 9 4.15e-35 TRUE
# ℹ 591 more rowsDann summieren wir die Wharscheinlichkeiten aller so amrkierten Ausgaben:
tibble( numSix = 0:600 ) %>%
mutate( prob = dbinom( numSix, 600, 1/6 ) ) %>%
mutate( as_or_even_less_likely = prob <= dbinom( 130, 600, 1/6 ) ) %>%
filter( as_or_even_less_likely ) %>%
summarise( sum(prob) )# A tibble: 1 × 1
`sum(prob)`
<dbl>
1 0.00146Die ist der p-Wert, den uns binom.test oben geliefert hat.
Grafishe Darstellung:
tibble( numSix = 60:150 ) %>%
mutate( prob = dbinom( numSix, 600, 1/6 ) ) %>%
mutate( prob_less_or_equal = prob < dbinom( 130, 600, 1/6 ) ) %>%
ggplot +
geom_col( aes( x=numSix, y=prob, fill=prob_less_or_equal ) ) +
scale_y_continuous( limits=c( 0, .0075 ), oob = scales::rescale_none )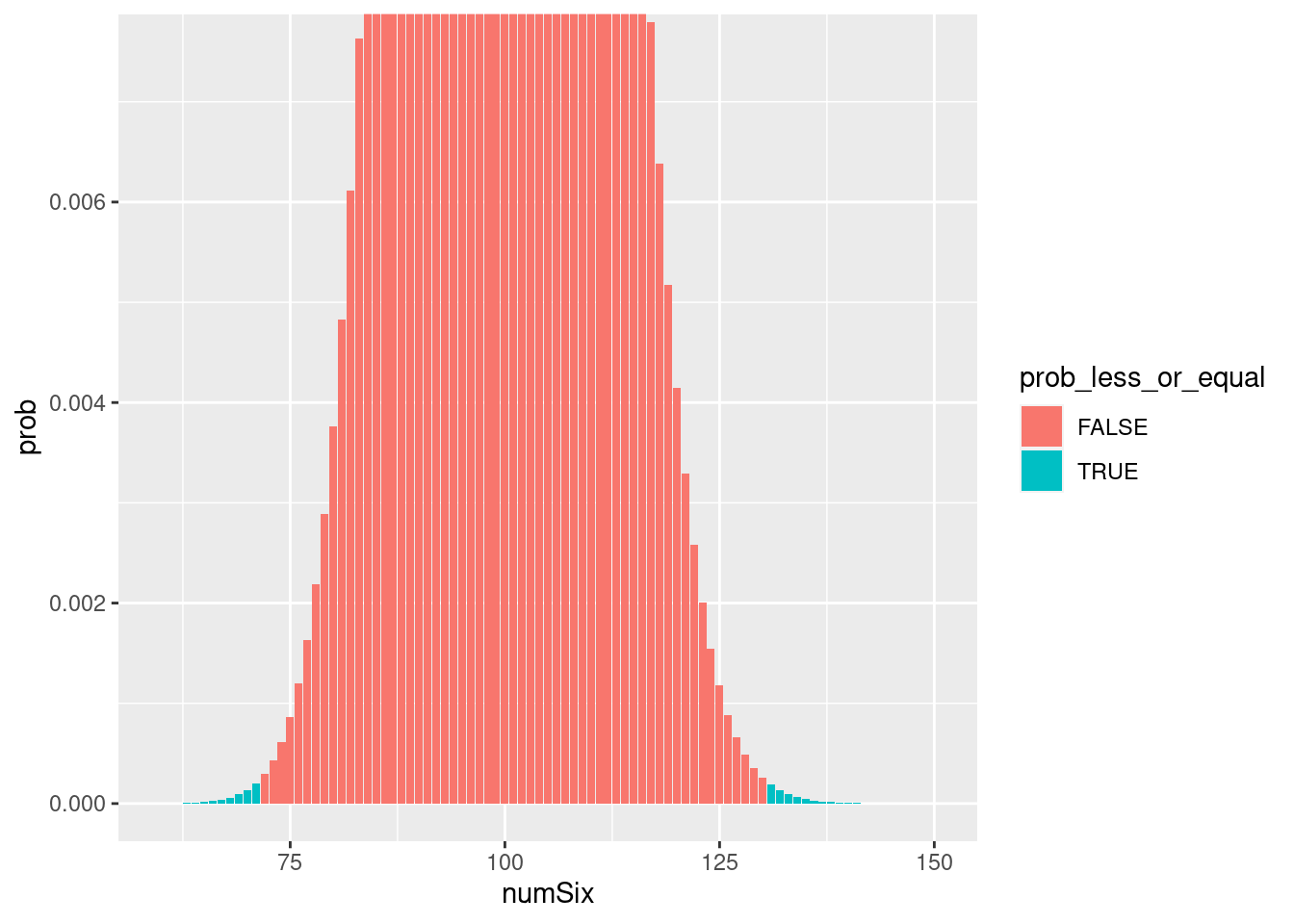
Dargestellt ist die Binomialverteilung für \(n=600\) und \(p=1/6\), mit Zoom auf den Fuß. Hellblau markiert alle Säulen, der Höhe kleiner oder gleich der Höhe der Säule bei \(k=130\) ist. Der p-Wert des zweiseitigen Binomialtest ist die Summe aller hellblauen Säulen. Beim einseitigen Test werden nur die Säulen auf einer Seite aufsummiert.
Weiteres Beispiel
Die Hilfe-Seite zu binom.test hat ein weiteres Beispiel, dass aus der Biologie stammt:
“Under (the assumption of) simple Mendelian inheritance, a cross between plants of two particular genotypes produces progeny 1/4 of which are”dwarf” and 3/4 of which are “giant”, respectively. In an experiment to determine if this assumption is reasonable, a cross results in progeny having 243 dwarf and 682 giant plants.”
(Als Quelle dieser Aufgabe ist das Buch “Practical nonparametric statistics” von W. J. Conover (Wiley, 1971), S. 97f, angegeben.)
Hier besteht kein Grund, einen einseiten Test zu verwenden, wir bleiben also beim Default von binom.test, dem zweiseitigen Test. Wir betrachten “dwarf” als Erfolg und “giant” als Fehlschlag. Die Erfolgswahrscheinlichkeit ist also unter der Nullhypothese Mendelscher Segregation 1/4.
binom.test( 243, 243+682, 1/4 )
Exact binomial test
data: 243 and 243 + 682
number of successes = 243, number of trials = 925, p-value = 0.3825
alternative hypothesis: true probability of success is not equal to 0.25
95 percent confidence interval:
0.2345934 0.2923317
sample estimates:
probability of success
0.2627027 Wenn wir den Phänotyp “giant” als Erfolg sehen, erhalten wir natürlich dasselbe Ergebnis:
binom.test( 682, 243+682, 3/4 )
Exact binomial test
data: 682 and 243 + 682
number of successes = 682, number of trials = 925, p-value = 0.3825
alternative hypothesis: true probability of success is not equal to 0.75
95 percent confidence interval:
0.7076683 0.7654066
sample estimates:
probability of success
0.7372973 Auch unter Annahme der Nullhypthese (nämlich: “Der phänotypische Trait segregiert Mendelsch im Verhältnis 3:1”) ist die Wahrscheinlichkeit, dass die Segretation so extrem wie beobachtet oder noch extremer vom erwarteten Verhältnis abweicht, 38%. Die Nullhypothese kann also nicht verworfen werden.
Das heißt aber nicht, das wir folgern dürfen, dass der Trait mendelsch vererbt wird.
Um das zu sehen, nehmen wir an, dass der Versuch wiederholt wird, aber mit 10 mal mehr Pflanzen, und dann genau dasselben Verhältnis, also 1430 : 6820 beobachtet wird.
Dann erhalten wir:
binom.test( 6820, 2430+6820, 3/4 )
Exact binomial test
data: 6820 and 2430 + 6820
number of successes = 6820, number of trials = 9250, p-value = 0.004961
alternative hypothesis: true probability of success is not equal to 0.75
95 percent confidence interval:
0.7282007 0.7462442
sample estimates:
probability of success
0.7372973 Nun liegt der p-Wert unter 1%. Dieser größere Versuch liefert also nun klare Hinweise auf eine kleine, aber statistisch signifikante, Abweichung vom Mendelschen Verhältnis.
Mit diesem Resultat würden wir also folgern: Es gibt mindestens zwei Gene, die den Phänotyp beeinflusst, und zwischen den beiden Genen gibt es ein zumindest leichtes Linkage-Disequilibrium.
Aus dem ursprünglichen Resultat dürfen wir also gar nichts folgern!
Einschub zur Terminologie: Anteile und Verhältnisse
Hüten Sie sich davor, die Begriffe “Anteil” (engl. “fraction”) und “Verhältnis” (engl. “ratio”) zu verwechseln.
Beispiel: Bei Mendelscher Segregation ist der erwartete Anteil des rezessiven Phänotyp in der F2-Population 1/4, d.h. 1/4 der F2-Population hat den rezessiven Phänotyp und der Anteil des dominanten Phänotypen ist 3/4 der Gesamt-Population. Das Verhältnis dominant-zu-rezessiv beträgt also 1:3.
Allgemein: Wie sagen Anteil (fraction), wenn wir einen Teil durch das Ganze teilen, und Verhältnis (ratio), wenn wir zwei Teile durcheinander teilen.
Anteile schreibt man mit Bruchstrich, Verhältnisse mit Doppelpunkt.
Also: “Reiner Alkohol wird mit Wasser im Verhältnis 1:9 gemischt” führt zu “Der Anteil an Alkohol in der Mischung ist 1/10.”
Ebenso wie Anteil werden verwendet die Begriffe “Bruchteil” und “Häufigkeit” verwendet.
Der englische Begriff proportion wird in der Statstik meist in der Bedeutung “Anteil” verwendet, in anderen Bereichen der Mathematik aber egher in der Bedeutung “Verhältnis”.
Der Begriff quotient seht meist für ein Verhältnis.
Einschub: Nochmals Simulation von Binomialverteilungen
Ganz oben haben wir den Versuch, einen Würfel 20 mal zu werfen, und die Sechsen zu zählen, wie folgt simuliert
sum( runif(20) < 1/6 )[1] 2Wir können das auch so schreiben:
rbinom( 1, 20, 1/6 )[1] 3Um den Versuch 30 mal zu wiederholen, schreiben wir
replicate( 30, sum( runif(20) < 1/6 ) ) [1] 5 4 2 5 4 2 3 1 3 3 3 1 2 3 2 2 2 3 1 0 0 4 2 2 3 9 2 5 3 2oder
rbinom( 30, 20, 1/6 ) [1] 3 2 2 2 2 7 0 2 2 4 5 2 3 5 1 4 5 4 6 4 2 3 3 2 6 1 2 4 6 4Beides gibt uns die Anzahl \(k\) der Sechsen, nachdem 30-mal simuliert wurde, dass je \(n=20\) Benoulli-Versuche (Würfe) durchgeführt und die Anzahl \(k\) der Erfolge jeweils gezählt wurden, wobei die Wahrscheinlichkeit eines Erolgs \(p=1/6\) betrug.
rbinom ist aber deutlich schneller, was man merkt, wenn man statt 30 viele 1000 Wiederholungen braucht.
Momente der Normalverteilung
Wiederholung: Verteilung
Betrachten wir nochmals die Binomialverteilung für \(n=600\) Würfe mit Erfolgs-Wahrscheinlichkeit \(p=1/6\). Die Wahrscheinlichkeit, genau \(k\) Erfolge zu erzielen, erhalten wir duch dbinom( k, n, p ).
Wir simulieren 10000 Werte für k:
n <- 600
p <- 1/6
k <- rbinom( 10000, n, p )
head( k, 50 ) # Zeige nur die ersten 50 der 10000 Werte [1] 104 98 93 94 115 99 85 99 109 94 101 96 114 100 94 96 106 100 106
[20] 105 98 108 100 97 97 104 85 103 95 107 106 105 108 91 88 99 113 96
[39] 108 98 109 94 113 106 100 107 76 105 100 97Wie oft ist \(k=112\)?
Zunächst der Anteil in der Stichprobe:
mean( k == 112 )[1] 0.0175Nun die exakte Wahrscheinlichkeit
dbinom( 112, n, p )[1] 0.01806759Mittelwert
Was ist der Mittelwert der Stichprobe?
mean(k)[1] 99.9569Welchen Mittelwert erwarten wir? Natürlich \(\mu=np=600\cdot\frac{1}{6}=100\):
Allgemein also: Der Erwartungswert der Binomialverteilung mit Versuchszahl \(n\) und Erfolgswahrscheinlichkeit \(p\) ist \(\mu=np\).
Varianz und Standardabweichung
Die erwartete Varianz einer Binomialverteilung mit Versuchszahl \(n\) und Erfolgswahrscheinlichkeit \(p\) ist \(v=np(1-p)\).
(Die Begründung überspringen wir; Sie finden sie in jedem einführendem lehrbuch der Statistik.)
Bei uns also: \(p=np(1-p)=100\cdot\frac{1}{6}\frac{5}{6}=500/36=83\frac{1}{3}\). In R:
n * p * (1-p)[1] 83.33333Die Stichproben-Varianz liegt dem erwarteten Wert recht nahe:
Was ist die varianz der Stichprobe?
var(k)[1] 84.32808Die Standardabweiochung ist die Wurzel der Varianz:
sqrt( n * p * (1-p) )[1] 9.128709In der simulierten Stichprobe
sd( k )[1] 9.183032Näherung der Binomialverteilung durch die Normalverteilung
Wie oben erwähnt, ergibt sich aus dem Zentralen Grenzwertsatz, dass die Binomialverteilung für großes \(n\) der Normalverteilung recht nahe kommt.
Wir überzeugen uns davon durch ein paar Grafiken.
Zunächst ein Histogramm der Stichprobe von eben:
hist( k )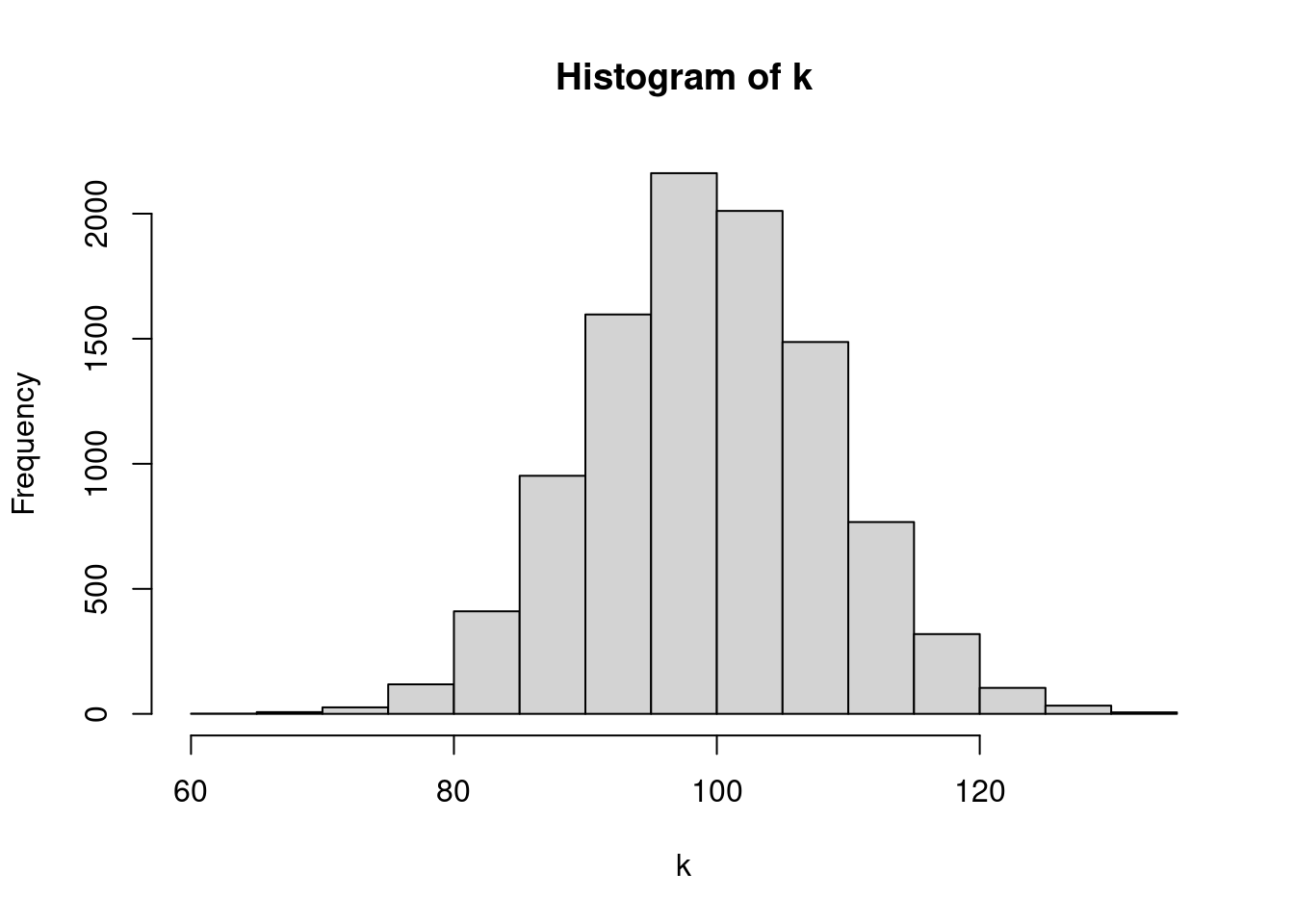
Wenn wir für jeden einzelnen Wert einen eigenen Balken verwenden, wird es feiner, aber rauher:
tibble( k ) %>%
group_by( k ) %>%
summarise( n=n() ) %>%
mutate( ) # A tibble: 68 × 2
k n
<int> <int>
1 62 1
2 67 1
3 68 2
4 69 2
5 70 2
6 71 1
7 72 3
8 73 6
9 74 2
10 75 14
# ℹ 58 more rowsggplot +
geom_col( aes( x=k, y=n/sum(n) ) )NULLHier ist dasselbe Diagramm, mit berechneten Wahrscheinlichkeiten statt Häufigkeiten in einer simulierten Stichprobe:
tibble( k = 60:140 ) %>%
mutate( p_binom = dbinom( k, 600, 1/6 ) ) %>%
ggplot + geom_col( aes( x=k, y=p ) )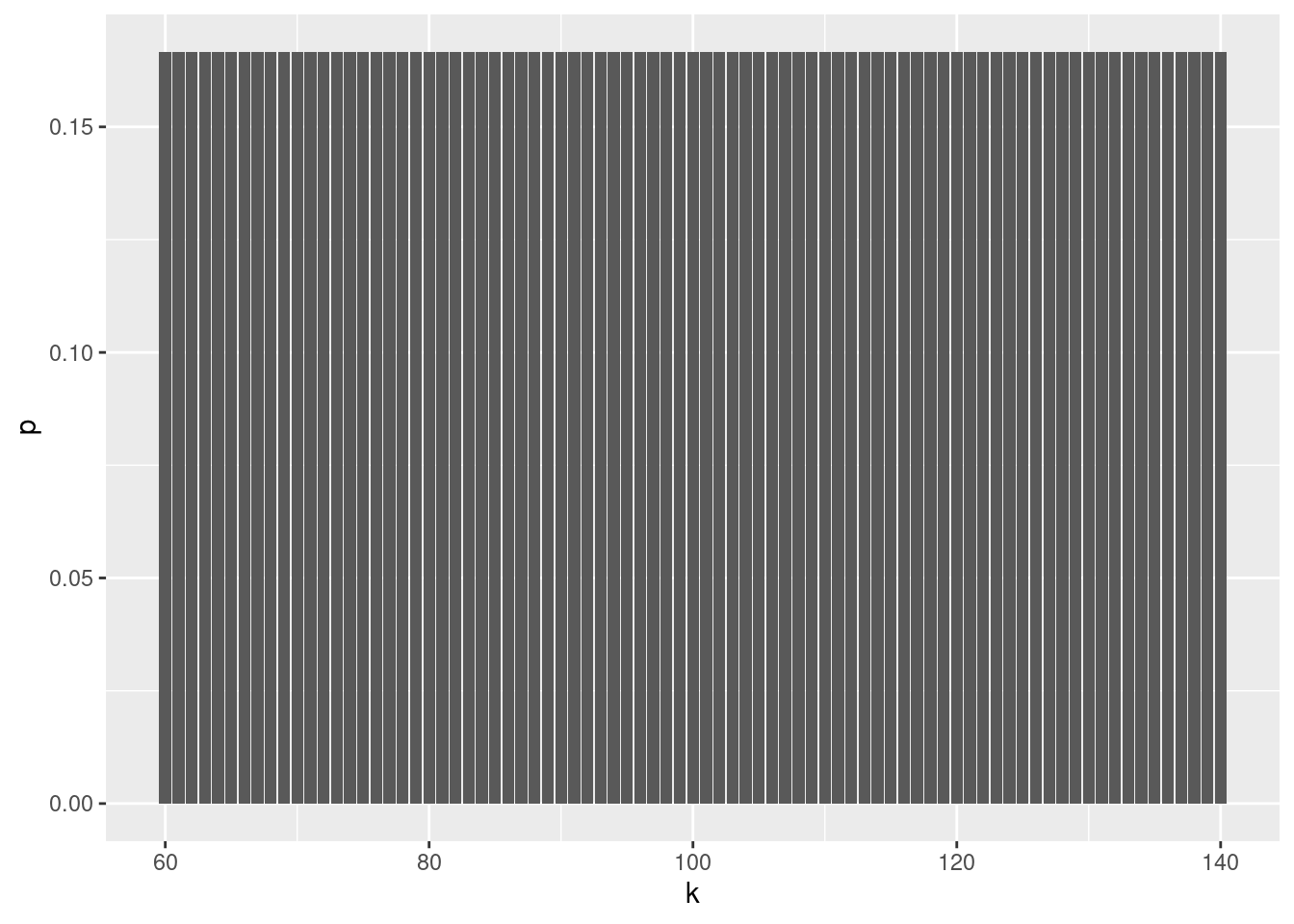
Wir berechnen Erwartungswert und Varianz der Binomialvberteilung und zeichnen in das Diagramm zusätzlich eine Normalverteilung ein, die denselben Mittelwert und dieselbe Varianz hat:
n <- 600
p <- 1/6
mu <- n*p
sd <- sqrt( n*p*(1-p) )
tibble( k = 60:140 ) %>%
mutate( p_binom = dbinom( k, size=n, prob=p ) ) %>%
mutate( p_norm = dnorm( k, mean=mu, sd=sd ) ) %>%
ggplot +
geom_col( aes( x=k, y=p_binom ) ) +
geom_point( aes( x=k, y=p_norm ), shape="plus", col="magenta" )
Wie wir sehen, ist der Unterschied zwischen Binomialverteilung (graue Balken) Normalverteilung (magenta Kreuze) nur sehr klein.
Allerdings ist die Binomialverteilung leicht asymmetrisch. Das liegt daran, dass ihr Wertebereich auf 0 bis \(n\) eingeschränkt ist, und ihr Erwartungswert \(\mu\) nicht in der Mitte des Wertebereichs liegt.
Bei kleinen Werten für \(n\) oder \(p\) passt das aber nicht so gut. Dazu zwei Beispiele:
Hier derselbe Code, aber für nur 10 Würfe:
n <- 10
p <- 1/6
mu <- n*p
sd <- sqrt( n*p*(1-p) )
tibble( k = 0:10 ) %>%
mutate( p_binom = dbinom( k, size=n, prob=p ) ) %>%
mutate( p_norm = dnorm( k, mean=mu, sd=sd ) ) %>%
ggplot +
geom_col( aes( x=k, y=p_binom ) ) +
geom_point( aes( x=k, y=p_norm ), shape="plus", col="magenta" )
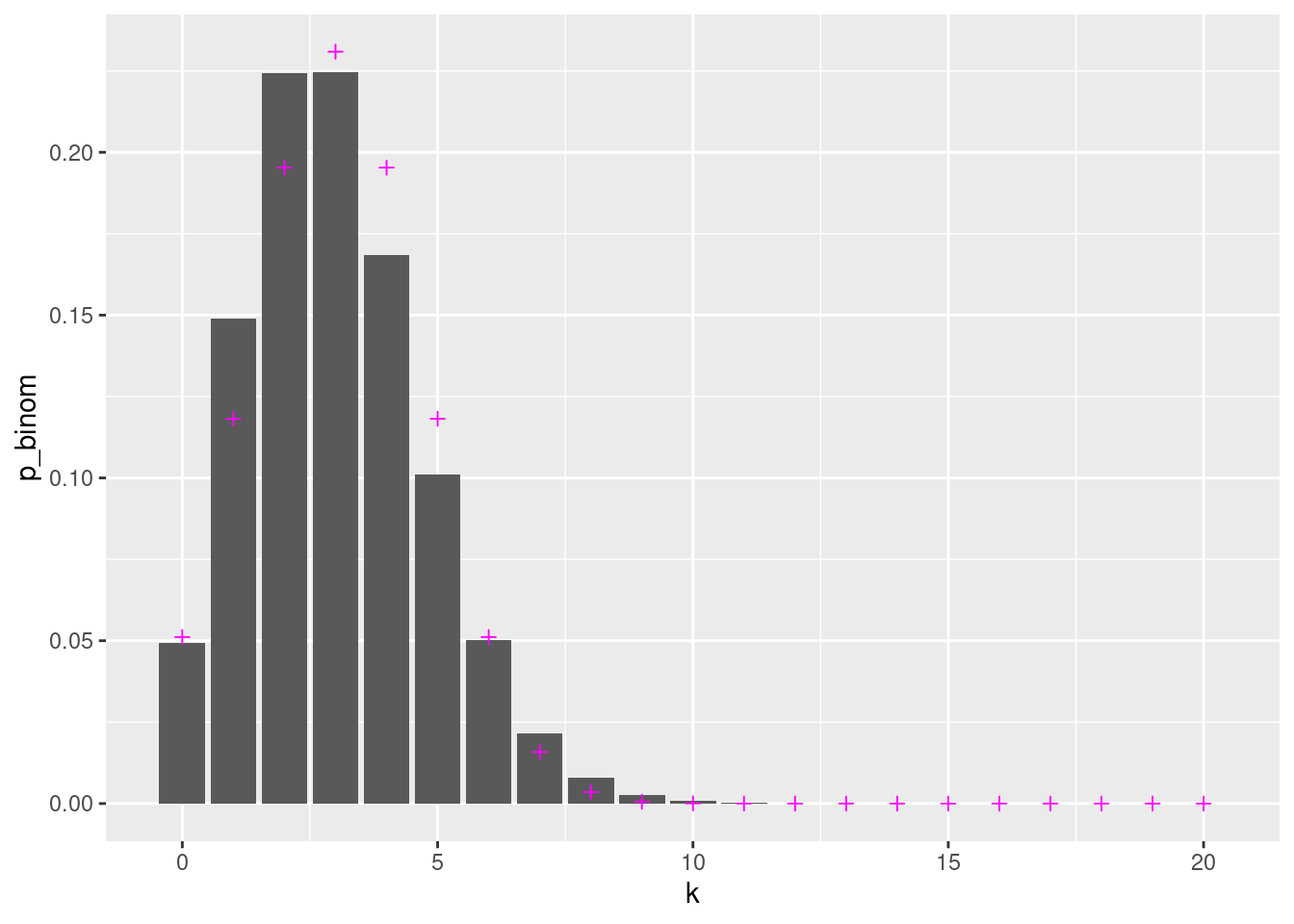
und hier nochmal für \(n=600\) aber mit Erfolgswahrscheinlichkeit \(p=1/200\) statt \(p=1/6\).
n <- 600
p <- .005
mu <- n*p
sd <- sqrt( n*p*(1-p) )
tibble( k = 0:20 ) %>%
mutate( p_binom = dbinom( k, size=n, prob=p ) ) %>%
mutate( p_norm = dnorm( k, mean=mu, sd=sd ) ) %>%
ggplot +
geom_col( aes( x=k, y=p_binom ) ) +
geom_point( aes( x=k, y=p_norm ), shape="plus", col="magenta" )